Алгоритм Гомори для частично целочисленной задачи линейного программирования
В частично целочисленных задачах требование целочисленности накладывается не на все переменные, а на одну или некоторые из них.Пусть дана следующая задача:
max {F(x)=∑cixi|∑ajixi{≤=≥}bj, j = 1,m, xi≥0 для всех i = 1,n}, (1)
целочисленной должна быть только переменная xk.
Таблица 1- симплекс-таблица для задачи ЛП
| базисные переменные | Свободные члены | Небазисные переменные | |||
| w1 | w2 | ... | wn | ||
| v1 | β1 | α11 | α12 | ... | α1n |
| v2 | β2 | α21 | α22 | ... | α2n |
| . | . | . | . | . | . |
| vm | βm | αm1 | αm2 | ... | αmn |
| F | β | c1 | c2 | ... | cn |
В результате решения задачи с отброшенным условием целочисленности получена оптимальная симплекс-таблица (табл. 1) и переменной xk соответствует строка базисной переменной vk этой таблицы. Эта строка порождает равенство
∑αkiwi+vk=βk. (2)
Выделим в βk целую и дробную часть и преобразуем (2) к виду
vk-[βk]={βk}-∑αkiwi (3)
Если значение vk = βk оказалось дробным, то можно сказать, что интервал [βk]<vk<[βk ]+1 не содержит допустимых целочисленных компонентов решения. Тогда для целочисленной переменной vk должно выполняться одно из двух неравенств: либо vk≤[βk], либо vk≥ [βk ] + 1. Левая часть выражения (3) должна быть целой.
Рассмотрим условия, при которых правая часть (3) будет принимать целое значение.
Если vk≤[βk ], то из (3) для αki≥ 0 следует, что
{βk}-∑αkiwi≤0 или ∑αkiwi≥{βk} (4)
Если vk≥[βk] + 1, то vk - [βk ] ≥ 1, и из (3) для αki≤0 следует, что
{βk}-∑αkiwi≥1 или ∑αkiwi≤{βk} -1 (5)
Умножим обе части неравенства (5) на
, тогда
(6)
Так как соотношения (4) и (6) не могут выполняться одновременно, их можно объединить в одно ограничение вида
(7)где I+ – множество значений i, для которых αki > 0 ; I- – множество значений i , для которых αki< 0.
Пример №1. Решить задачу частично целочисленного линейного программирования.
Считать, что базисные переменные в оптимальной симплекс-таблице (до поиска целочисленного решения) должны быть целочисленными. По этой же таблице указать решение двойственной задачи; проверить ответ с помощью базисного вектора С0.
Решим задачу частично целочисленного линейного программирования симплексным методом, с использованием калькулятора. Определим максимальное значение целевой функции F(X) = 7x1 + 9x2 при следующих условиях-ограничений.
- x1 + 3x2 + x3=6
7x1 + x2 + x4=35
Для построения первого опорного плана в системе уравнений уже имеются базисные переменные.
-1x1 + 3x2 + 1x3 + 0x4 = 6
7x1 + 1x2 + 0x3 + 1x4 = 35
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
| A = |
|
Экономический смысл дополнительных переменных: дополнительные перемены задачи ЛП обозначают излишки сырья, времени, других ресурсов, остающихся в производстве данного оптимального плана.
Решим систему уравнений относительно базисных переменных: x3, x4
Полагая, что свободные переменные равны 0, получим первый опорный план:
X1 = (0,0,6,35)
Базисное решение называется допустимым, если оно неотрицательно.
| Базис | B | x1 | x2 | x3 | x4 |
| x3 | 6 | -1 | 3 | 1 | 0 |
| x4 | 35 | 7 | 1 | 0 | 1 |
| F(X0) | 0 | -7 | -9 | 0 | 0 |
Итерация №0.
1. Проверка критерия оптимальности.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
2. Определение новой базисной переменной.
В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент по модулю.
3. Определение новой свободной переменной.
Вычислим значения Di по строкам как частное от деления: bi / ai2
и из них выберем наименьшее:
min (6 : 3 , 35 : 1 ) = 2
Следовательно, 1-ая строка является ведущей.
Разрешающий элемент равен (3) и находится на пересечении ведущего столбца и ведущей строки.
| Базис | B | x1 | x2 | x3 | x4 | min |
| x3 | 6 | -1 | 3 | 1 | 0 | 2 |
| x4 | 35 | 7 | 1 | 0 | 1 | 35 |
| F(X1) | 0 | -7 | -9 | 0 | 0 | 0 |
Формируем следующую часть симплексной таблицы.
Вместо переменной x3 в план 1 войдет переменная x2.
Строка, соответствующая переменной x2 в плане 1, получена в результате деления всех элементов строки x3 плана 0 на разрешающий элемент РЭ=3
На месте разрешающего элемента в плане 1 получаем 1.
В остальных клетках столбца x2 плана 1 записываем нули.
Таким образом, в новом плане 1 заполнены строка x2 и столбец x2.
Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника.
Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ - (А*В)/РЭ
СТЭ - элемент старого плана, РЭ - разрешающий элемент (3), А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:
| B | x 1 | x 2 | x 3 | x 4 |
| 6 : 3 | -1 : 3 | 3 : 3 | 1 : 3 | 0 : 3 |
| 35-(6 • 1):3 | 7-(-1 • 1):3 | 1-(3 • 1):3 | 0-(1 • 1):3 | 1-(0 • 1):3 |
| 0-(6 • -9):3 | -7-(-1 • -9):3 | -9-(3 • -9):3 | 0-(1 • -9):3 | 0-(0 • -9):3 |
| Базис | B | x1 | x2 | x3 | x4 |
| x2 | 2 | -1/3 | 1 | 1/3 | 0 |
| x4 | 33 | 22/3 | 0 | -1/3 | 1 |
| F(X1) | 18 | -10 | 0 | 3 | 0 |
1. Проверка критерия оптимальности.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
2. Определение новой базисной переменной.
В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент по модулю.
3. Определение новой свободной переменной.
Вычислим значения Di по строкам как частное от деления: bi / ai1
и из них выберем наименьшее:
min (- , 33 : 71/3 ) = 41/2
Следовательно, 2-ая строка является ведущей.
Разрешающий элемент равен (71/3) и находится на пересечении ведущего столбца и ведущей строки.
| Базис | B | x1 | x2 | x3 | x4 | min |
| x2 | 2 | -1/3 | 1 | 1/3 | 0 | - |
| x4 | 33 | 71/3 | 0 | -1/3 | 1 | 41/2 |
| F(X2) | 18 | -10 | 0 | 3 | 0 | 0 |
Формируем следующую часть симплексной таблицы.
Вместо переменной x4 в план 2 войдет переменная x1.
Строка, соответствующая переменной x1 в плане 2, получена в результате деления всех элементов строки x4 плана 1 на разрешающий элемент РЭ=71/3
На месте разрешающего элемента в плане 2 получаем 1.
В остальных клетках столбца x1 плана 2 записываем нули.
Таким образом, в новом плане 2 заполнены строка x1 и столбец x1.
Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника.
Представим расчет каждого элемента в виде таблицы:
| B | x 1 | x 2 | x 3 | x 4 |
| 2-(33 • -1/3):71/3 | -1/3-(71/3 • -1/3):71/3 | 1-(0 • -1/3):71/3 | 1/3-(-1/3 • -1/3):71/3 | 0-(1 • -1/3):71/3 |
| 33 : 71/3 | 71/3 : 71/3 | 0 : 71/3 | -1/3 : 71/3 | 1 : 71/3 |
| 18-(33 • -10):71/3 | -10-(71/3 • -10):71/3 | 0-(0 • -10):71/3 | 3-(-1/3 • -10):71/3 | 0-(1 • -10):71/3 |
| Базис | B | x1 | x2 | x3 | x4 |
| x2 | 7/2 | 0 | 1 | 7/22 | 1/22 |
| x1 | 9/2 | 1 | 0 | -1/22 | 3/22 |
| F(X2) | 63 | 0 | 0 | 28/11 | 15/11 |
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.
Окончательный вариант симплекс-таблицы:
| Базис | B | x1 | x2 | x3 | x4 |
| x2 | 7/2 | 0 | 1 | 7/22 | 1/22 |
| x1 | 9/2 | 1 | 0 | -1/22 | 3/22 |
| F(X3) | 63 | 0 | 0 | 28/11 | 15/11 |
Метод Гомори.
В полученном оптимальном плане переменная x2 имеет дробную часть числа. Дополнительное ограничение составляем по строке, соответствующей переменной x2.
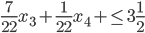
После преобразования, умножения его на (-1) и введения дополнительной переменной х5 получим дополнительное ограничение в виде
-7/22x3-1/22x4+x5 = -1/2
Поскольку двойственный симплекс-метод используется для поиска минимума целевой функции, делаем преобразование F(x) = -F(X).
| Базис | B | x1 | x2 | x3 | x4 | x5 |
| x2 | 7/2 | 0 | 1 | 7/22 | 1/22 | 0 |
| x1 | 9/2 | 1 | 0 | -1/22 | 3/22 | 0 |
| x5 | -1/2 | 0 | 0 | -7/22 | -1/22 | 1 |
| F(X0) | -63 | 0 | 0 | -28/11 | -15/11 | 0 |
План 0 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец.
2. Определение новой свободной переменной.
Среди отрицательных значений базисных переменных выбираем наибольший по модулю.
Ведущей будет 3-ая строка, а переменную x5 следует вывести из базиса.
3. Определение новой базисной переменной.
Минимальное значение θ соответствует 3-му столбцу, т.е. переменную x3 необходимо ввести в базис.
На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный (-7/22).
| Базис | B | x1 | x2 | x3 | x4 | x5 |
| x2 | 31/2 | 0 | 1 | 7/22 | 1/22 | 0 |
| x1 | 41/2 | 1 | 0 | -1/22 | 3/22 | 0 |
| x5 | -1/2 | 0 | 0 | -7/22 | -1/22 | 1 |
| F(X0) | -63 | 0 | 0 | -26/11 | -14/11 | 0 |
| θ | - | - | -26/11 : (-7/22) = 8 | -14/11 : (-1/22) = 30 | - |
Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
| Базис | B | x1 | x2 | x3 | x4 | x5 |
| x2 | 3 | 0 | 1 | 0 | 0 | 1 |
| x1 | 32/7 | 1 | 0 | 0 | 1/7 | -1/7 |
| x3 | 11/7 | 0 | 0 | 1 | 1/7 | -22/7 |
| F(X0) | -59 | 0 | 0 | 0 | -1 | -8 |
| B | x 1 | x 2 | x 3 | x 4 | x 5 |
| 31/2-(-1/2 • 7/22):-7/22 | 0-(0 • 7/22):-7/22 | 1-(0 • 7/22):-7/22 | 7/22-(-7/22 • 7/22):-7/22 | 1/22-(-1/22 • 7/22):-7/22 | 0-(1 • 7/22):-7/22 |
| 41/2-(-1/2 • -1/22):-7/22 | 1-(0 • -1/22):-7/22 | 0-(0 • -1/22):-7/22 | -1/22-(-7/22 • -1/22):-7/22 | 3/22-(-1/22 • -1/22):-7/22 | 0-(1 • -1/22):-7/22 |
| -1/2 : -7/22 | 0 : -7/22 | 0 : -7/22 | -7/22 : -7/22 | -1/22 : -7/22 | 1 : -7/22 |
| -63-(-1/2 • -26/11):-7/22 | 0-(0 • -26/11):-7/22 | 0-(0 • (-2)6/11):-7/22 | -26/11-(-7/22 • -26/11):-7/22 | -14/11-(-1/22 • -26/11):-7/22 | 0-(1 • -26/11):-7/22 |
Перейти к онлайн решению своей задачи
Пример №2.
Определим минимальное значение целевой функции F(X) = 6x1 + 8x2 + x3 + 2x4 при следующих условиях-ограничений.
x1 + 2x2 - x3≥3
2x1 + x2 + x3 + x4≥4
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
В 1-м неравенстве смысла (≥) вводим базисную переменную x5 со знаком минус. В 2-м неравенстве смысла (≥) вводим базисную переменную x6 со знаком минус.
1x1 + 2x2-1x3 + 0x4-1x5 + 0x6 = 3
2x1 + 1x2 + 1x3 + 1x4 + 0x5-1x6 = 4
Умножим все строки на (-1) и будем искать первоначальный опорный план.
-1x1-2x2 + 1x3 + 0x4 + 1x5 + 0x6 = -3
-2x1-1x2-1x3-1x4 + 0x5 + 1x6 = -4
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
| A = |
|
Экономический смысл дополнительных переменных: дополнительные перемены задачи ЛП обозначают излишки сырья, времени, других ресурсов, остающихся в производстве данного оптимального плана.
Решим систему уравнений относительно базисных переменных: x5, x6
Полагая, что свободные переменные равны 0, получим первый опорный план:
X1 = (0,0,0,0,-3,-4)
Базисное решение называется допустимым, если оно неотрицательно.
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
| x5 | -3 | -1 | -2 | 1 | 0 | 1 | 0 |
| x6 | -4 | -2 | -1 | -1 | -1 | 0 | 1 |
| F(X0) | 0 | 6 | 8 | 1 | 2 | 0 | 0 |
План 0 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец.
2. Определение новой свободной переменной.
Среди отрицательных значений базисных переменных выбираем наибольший по модулю.
Ведущей будет 2-ая строка, а переменную x6 следует вывести из базиса.
3. Определение новой базисной переменной.
Минимальное значение θ соответствует 4-му столбцу, т.е. переменную x4 необходимо ввести в базис.
На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный (-1).
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
| x5 | -3 | -1 | -2 | 1 | 0 | 1 | 0 |
| x6 | -4 | -2 | -1 | -1 | -1 | 0 | 1 |
| F(X0) | 0 | 6 | 8 | 1 | 2 | 0 | 0 |
| θ | 6 : (-2) = -3 | 8 : (-1) = -8 | 1 : (-1) = -1 | 2 : (-1) = -2 | - | - |
Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
| x5 | -3 | -1 | -2 | 1 | 0 | 1 | 0 |
| x4 | 4 | 2 | 1 | 1 | 1 | 0 | -1 |
| F(X0) | -8 | 2 | 6 | -1 | 0 | 0 | 2 |
| B | x 1 | x 2 | x 3 | x 4 | x 5 | x 6 |
| -3-(-4 • 0):-1 | -1-(-2 • 0):-1 | -2-(-1 • 0):-1 | 1-(-1 • 0):-1 | 0-(-1 • 0):-1 | 1-(0 • 0):-1 | 0-(1 • 0):-1 |
| -4 : -1 | -2 : -1 | -1 : -1 | -1 : -1 | -1 : -1 | 0 : -1 | 1 : -1 |
| 0-(-4 • 2):-1 | 6-(-2 • 2):-1 | 8-(-1 • 2):-1 | 1-(-1 • 2):-1 | 2-(-1 • 2):-1 | 0-(0 • 2):-1 | 0-(1 • 2):-1 |
План 1 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец.
2. Определение новой свободной переменной.
Среди отрицательных значений базисных переменных выбираем наибольший по модулю.
Ведущей будет 1-ая строка, а переменную x5 следует вывести из базиса.
3. Определение новой базисной переменной.
Минимальное значение θ соответствует 2-му столбцу, т.е. переменную x2 необходимо ввести в базис.
На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный (-2).
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
| x5 | -3 | -1 | -2 | 1 | 0 | 1 | 0 |
| x4 | 4 | 2 | 1 | 1 | 1 | 0 | -1 |
| F(X0) | -8 | 2 | 6 | -1 | 0 | 0 | 2 |
| θ | 2 : (-1) = -2 | 6 : (-2) = -3 | - | - | - | - |
Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
| x2 | 3/2 | 1/2 | 1 | -1/2 | 0 | -1/2 | 0 |
| x4 | 5/2 | 3/2 | 0 | 3/2 | 1 | 1/2 | -1 |
| F(X1) | -17 | -1 | 0 | 2 | 0 | 3 | 2 |
| B | x 1 | x 2 | x 3 | x 4 | x 5 | x 6 |
| -3 : -2 | -1 : -2 | -2 : -2 | 1 : -2 | 0 : -2 | 1 : -2 | 0 : -2 |
| 4-(-3 • 1):-2 | 2-(-1 • 1):-2 | 1-(-2 • 1):-2 | 1-(1 • 1):-2 | 1-(0 • 1):-2 | 0-(1 • 1):-2 | -1-(0 • 1):-2 |
| -8-(-3 • 6):-2 | 2-(-1 • 6):-2 | 6-(-2 • 6):-2 | -1-(1 • 6):-2 | 0-(0 • 6):-2 | 0-(1 • 6):-2 | 2-(0 • 6):-2 |
Переходим к основному алгоритму симплекс-метода.
Итерация №0.
1. Проверка критерия оптимальности.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
2. Определение новой базисной переменной.
В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент по модулю.
3. Определение новой свободной переменной.
Вычислим значения Di по строкам как частное от деления: bi / ai1
и из них выберем наименьшее:
min (11/2 : 1/2 , 21/2 : 11/2 ) = 12/3
Следовательно, 2-ая строка является ведущей.
Разрешающий элемент равен (11/2) и находится на пересечении ведущего столбца и ведущей строки.
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | min |
| x2 | 11/2 | 1/2 | 1 | -1/2 | 0 | -1/2 | 0 | 3 |
| x4 | 21/2 | 11/2 | 0 | 11/2 | 1 | 1/2 | -1 | 12/3 |
| F(X1) | -17 | -1 | 0 | 2 | 0 | 3 | 2 | 0 |
Формируем следующую часть симплексной таблицы.
Вместо переменной x4 в план 1 войдет переменная x1.
Строка, соответствующая переменной x1 в плане 1, получена в результате деления всех элементов строки x4 плана 0 на разрешающий элемент РЭ=11/2
На месте разрешающего элемента в плане 1 получаем 1.
В остальных клетках столбца x1 плана 1 записываем нули.
Таким образом, в новом плане 1 заполнены строка x1 и столбец x1.
Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника.
Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ - (А*В)/РЭ
СТЭ - элемент старого плана, РЭ - разрешающий элемент (11/2), А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:
| B | x 1 | x 2 | x 3 | x 4 | x 5 | x 6 |
| 11/2-(21/2 • 1/2):11/2 | 1/2-(11/2 • 1/2):11/2 | 1-(0 • 1/2):11/2 | -1/2-(11/2 • 1/2):11/2 | 0-(1 • 1/2):11/2 | -1/2-(1/2 • 1/2):11/2 | 0-(-1 • 1/2):11/2 |
| 21/2 : 11/2 | 11/2 : 11/2 | 0 : 11/2 | 11/2 : 11/2 | 1 : 11/2 | 1/2 : 11/2 | -1 : 11/2 |
| -17-(21/2 • -1):11/2 | -1-(11/2 • -1):11/2 | 0-(0 • -1):11/2 | 2-(11/2 • -1):11/2 | 0-(1 • -1):11/2 | 3-(1/2 • -1):11/2 | 2-(-1 • -1):11/2 |
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
| x2 | 2/3 | 0 | 1 | -1 | -1/3 | -2/3 | 1/3 |
| x1 | 5/3 | 1 | 0 | 1 | 2/3 | 1/3 | -2/3 |
| F(X1) | -46/3 | 0 | 0 | 3 | 2/3 | 10/3 | 4/3 |
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.
Окончательный вариант симплекс-таблицы:
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
| x2 | 2/3 | 0 | 1 | -1 | -1/3 | -2/3 | 1/3 |
| x1 | 5/3 | 1 | 0 | 1 | 2/3 | 1/3 | -2/3 |
| F(X2) | -46/3 | 0 | 0 | 3 | 2/3 | 10/3 | 4/3 |
Метод Гомори.
В полученном оптимальном плане переменная x1 имеет дробную часть числа. Дополнительное ограничение составляем по строке, соответствующей переменной x1.
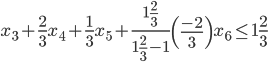
После преобразования, умножения его на (-1) и введения дополнительной переменной х7 получим дополнительное ограничение в виде
-x3-2/3x4-1/3x5-11/3x6+x7 = -2/3
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| x2 | 2/3 | 0 | 1 | -1 | -1/3 | -2/3 | 1/3 | 0 |
| x1 | 5/3 | 1 | 0 | 1 | 2/3 | 1/3 | -2/3 | 0 |
| x7 | -2/3 | 0 | 0 | -1 | -2/3 | -1/3 | -4/3 | 1 |
| F(X0) | -46/3 | 0 | 0 | 3 | 2/3 | 10/3 | 4/3 | 0 |
План 0 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец.
2. Определение новой свободной переменной.
Среди отрицательных значений базисных переменных выбираем наибольший по модулю.
Ведущей будет 3-ая строка, а переменную x7 следует вывести из базиса.
3. Определение новой базисной переменной.
Минимальное значение θ соответствует 6-му столбцу, т.е. переменную x6 необходимо ввести в базис.
На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный (-11/3).
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| x2 | 2/3 | 0 | 1 | -1 | -1/3 | -2/3 | 1/3 | 0 |
| x1 | 12/3 | 1 | 0 | 1 | 2/3 | 1/3 | -2/3 | 0 |
| x7 | -2/3 | 0 | 0 | -1 | -2/3 | -1/3 | -11/3 | 1 |
| F(X0) | -151/3 | 0 | 0 | 3 | 2/3 | 31/3 | 11/3 | 0 |
| θ | - | - | 3 : (-1) = -3 | 2/3 : (-2/3) = -1 | 31/3 : (-1/3) = -10 | 11/3 : (-11/3) = -1 | - |
Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| x2 | 1/2 | 0 | 1 | -5/4 | -1/2 | -3/4 | 0 | 1/4 |
| x1 | 2 | 1 | 0 | 3/2 | 1 | 1/2 | 0 | -1/2 |
| x6 | 1/2 | 0 | 0 | 3/4 | 1/2 | 1/4 | 1 | -3/4 |
| F(X0) | -16 | 0 | 0 | 2 | 0 | 3 | 0 | 1 |
| B | x 1 | x 2 | x 3 | x 4 | x 5 | x 6 | x 7 |
| 2/3-(-2/3 • 1/3):-11/3 | 0-(0 • 1/3):-11/3 | 1-(0 • 1/3):-11/3 | -1-(-1 • 1/3):-11/3 | -1/3-(-2/3 • 1/3):-11/3 | -2/3-(-1/3 • 1/3):-11/3 | 1/3-(-11/3 • 1/3):-11/3 | 0-(1 • 1/3):-11/3 |
| 12/3-(-2/3 • -2/3):-11/3 | 1-(0 • -2/3):-11/3 | 0-(0 • -2/3):-11/3 | 1-(-1 • -2/3):-11/3 | 2/3-(-2/3 • -2/3):-11/3 | 1/3-(-1/3 • -2/3):-11/3 | -2/3-(-11/3 • -2/3):-11/3 | 0-(1 • -2/3):-11/3 |
| -2/3 : -11/3 | 0 : -11/3 | 0 : -11/3 | -1 : -11/3 | -2/3 : -11/3 | -1/3 : -11/3 | -11/3 : -11/3 | 1 : -11/3 |
| -151/3-(-2/3 • 11/3):-11/3 | 0-(0 • 11/3):-11/3 | 0-(0 • 11/3):-11/3 | 3-(-1 • 11/3):-11/3 | 2/3-(-2/3 • 11/3):-11/3 | 31/3-(-1/3 • 11/3):-11/3 | 11/3-(-11/3 • 11/3):-11/3 | 0-(1 • 11/3):-11/3 |
