Вычисление определителей методом декомпозиции
Рассмотрим ещё один алгоритм вычисления определителя квадратной матрицы. Этот алгоритм основан на идее представления исходной матрицы в виде произведения двух треугольных матриц. Пусть задана квадратная матрица: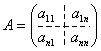 .
.
Представим A в виде:
A = BC,
где
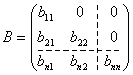
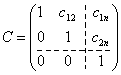 .
.
Тогда
 .
.
Как вычислить элементы матриц B и C? Перемножая матрицы B и C и приравнивая элементы матрицы - произведения соответствующим элементам матрицы A получим следующие вычислительные формулы:

Пример решения с использованием калькулятора.
Суть алгоритма декомпозиции основана на идее представления исходной матрицы в виде произведения двух треугольных матриц. Пусть задана квадратная матрица:
Представим A в виде: A=BC
Тогда detA=b11 • b22 • b33
Покажем пример вычислений нескольких значений матриц B и C.
Вычисляем значение элемента b11=-1
c11=-1/(-1)=1
c12=4/(-1)=-4
c13=3/(-1)=-3
Вычисляем значение элемента b21=2
Вычисляем значение элемента b22=0 - (2 • -4)=8
c22=8/8=1
c23=15/8=1.88
Вычисляем значение элемента b31=4
Вычисляем значение элемента b32=5 - (4 • -4)=21
Вычисляем значение элемента b33=-3 - (4 • -3 + 21 • 1.88)=-30.38
c33=-30.38/(-30.38)=1
detA=(-1) • 8 • (-30.38) = 243
Суть алгоритма декомпозиции основана на идее представления исходной матрицы в виде произведения двух треугольных матриц. Пусть задана квадратная матрица:
Представим A в виде: A=BC
Тогда detA=b11 • b22 • b33
Покажем пример вычислений нескольких значений матриц B и C.
Вычисляем значение элемента b11=-1
c11=-1/(-1)=1
c12=4/(-1)=-4
c13=3/(-1)=-3
Вычисляем значение элемента b21=2
Вычисляем значение элемента b22=0 - (2 • -4)=8
c22=8/8=1
c23=15/8=1.88
Вычисляем значение элемента b31=4
Вычисляем значение элемента b32=5 - (4 • -4)=21
Вычисляем значение элемента b33=-3 - (4 • -3 + 21 • 1.88)=-30.38
c33=-30.38/(-30.38)=1
| B= |
|
| C= |
|
detA=(-1) • 8 • (-30.38) = 243
Ответ: 243
