Комплексные числа

Комплексное число в тригонометрической форме:
z=|z|[cos(φ+2πk)+i·sin(φ+2πk)]

Комплексное число в показательной форме: z=|z|e^iφ
Угол φ называют аргументом числа z и обозначают Arg(z).

Назначение. Данный сервис предназначен для представления комплексного числа в тригонометрической и показательной формах в онлайн режиме. Результаты вычисления оформляются в формате Word.

Комплексное число должно быть представлено в алгебраическое форме z=x+i*y.

Правила ввода функции

Все математические операции выражаются через общепринятые символы +, -, *, /.
Примеры

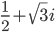≡ 1/2+sqrt(3)*I

Скачать пример отчета

Если 0 ≤ arg z ≤ 2π: 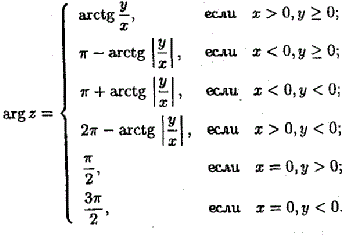$аргумент комплексного числа$

см. также Как извлечь корень из комплексного числа

Действия с комплексными числами

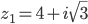
z₂=-1-i
Сложение комплексных чисел (отдельно складываются действительные и мнимые части)

Вычитание комплексных чисел (отдельно вычитаются действительные и мнимые части)

Умножение комплексных чисел

Деление комплексных чисел (подвести под общий знаменатель)

При умножении двух комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются. При делении комплексных чисел их модули делятся, а аргументы вычитаются.
z₁ = r₁(cos φ₁ + i sin φ₁), z₂ = r₂(cos φ₂ + i sin φ₂)
Тогда
z₁ · z₂ = r₁r₂[cos(φ₁ + φ₂)+ i sin(φ₁ + φ₂)]

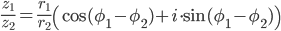
Что делать, если задано сложное комплексное выражение. Его можно упростить с помощью следующего правила. Например:

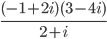
Необходимо умножить дробь на сопряженное выражение (2-i).

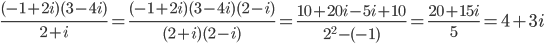
Возведение в степень. Формула Муавра

cⁿ=|cⁿ|·(cos n·φ+i·sin n·φ)

При возведении комплексного числа в натуральную степень, модуль возводится в эту степень, а аргумент умножается на показатель степени.

Пример. Найти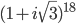
Решение.

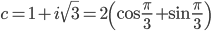
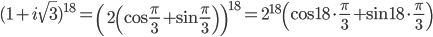=2¹⁸(cos 6π + i·sin 6π)=2¹⁸=262144

Что делать, если комплексное число необходимо возвести в большую степень. Например: (1+i)⁹⁸⁸. Достаточно это комплексное число сначала возвести во вторую степень:
(1+i)² = 2i, а затем (2i)^988/2 = (2i)⁴⁹⁴ = 2⁴⁹⁴i⁴⁹⁴ = 2⁴⁹⁴(-1)²⁴⁷ = -2⁴⁹⁴

Все вычисления с комплексными числами можно проверить в онлайн режиме.
Примечание:

abs - модуль комплексного числа |z|. Пример: abs(-5.5-6.6i)
arg - аргумент комплексного числа φ. Пример: arg(5.5+6.6i)

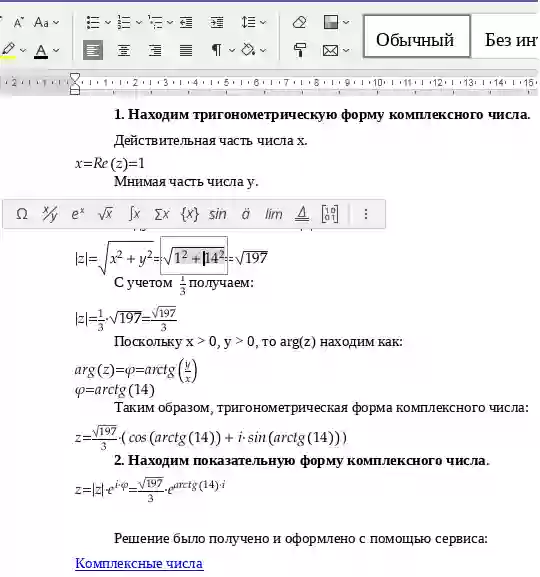
Пример №1. Записать комплексное число в тригонометрической форме.

z=-1-4i

Базовая формула:

z = |z|[cos(φ+2πk) + i sin(φ+2πk)]

где φ=arctg((-4)/(-1));
Алгоритм

находим угол φ.
находим модуль |z| = sqrt(x² + y²).

1. Находим тригонометрическую форму комплексного числа z=-1-4i
Действительная часть комплексного числа: x = Re(z) = -1
Мнимая часть: y = Im(z) = -4
Модуль комплексного числа равен:

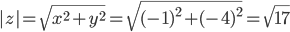
Поскольку x<0, y<0, то arg(z) находим как:

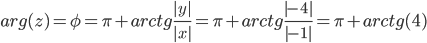
Таким образом, тригонометрическая форма комплексного числа z=-1-4i

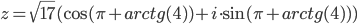
2. Находим показательную форму комплексного числа

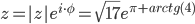
Пример №2. Как из тригонометрической формы комплексного числа преобразовать в алгебраическую форму.

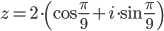
Модуль комплексного числа равен 2 ,т.е. 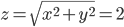или x²+y²=4
Аргумент комплексного числа
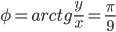или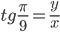
Получаем систему из двух уравнений:
x²+y²=4

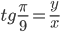
Выразим 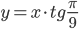и подставим в первое выражение:

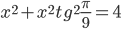
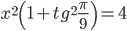
Поскольку 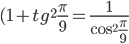, то получаем:
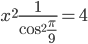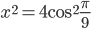или или .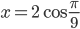

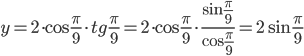
Таким образом, из выражения 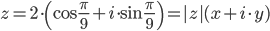можно сразу было получить:
,
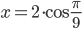