Подробный пример нахождения экстремума функции двух переменных
Перейти к онлайн решению своей задачиПример №1. Исследовать на экстремум функции двух переменных.
z = (x-2)2 + 3y2
Решение находим с помощью калькулятора.
z = (x-2)^2+3*y^2
1. Найдем частные производные.
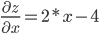
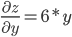
2. Решим систему уравнений.
2·x-4 = 0
6·y = 0
Из первого уравнения выражаем x:
x = 2
6·y = 0
Откуда y = 0
Количество критических точек равно 1: M1(2;0)
3. Найдем частные производные второго порядка.
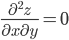
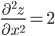
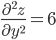
4. Вычислим значение этих частных производных второго порядка в критических точках M(x0;y0).
Вычисляем значения для точки M1(2;0)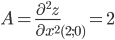
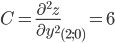
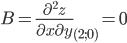
Поскольку AC - B2 = 12 > 0 и A > 0 , то в точке M1(2;0) имеется минимум z(2;0) = 0
Вывод: В точке M1(2;0) имеется минимум z(2;0) = 0;
Пример №2. Исследовать на экстремум функцию z=x3+3xy2-15x-12y
Решение.
1) Найдем частные производные:
dz/dx=3x2+3y2-15
dz/dy=6xy-12
2) тогда система для отыскания стационарных точек имеет вид
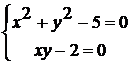 .
.
Решив систему, получим четыре стационарные точки:
P1(1,2), P2(2,1), P3(-1,-2), P4(-2,-1). Найдем производные 2-го порядка
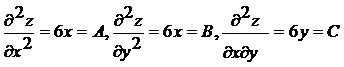
и составим дискриминант ∆AB-C2 для каждой стационарной точки.
1) Для точки P1(1,2) Δ=36-144<0, в P1(1,2) экстремума нет.
2) Для точки P2(2,1), Δ =144 – 36 >0, A>0, в P2(2,1)функция имеет минимум, zmin = -28
3) Для точки P3(-1,-2), Δ = 36-144 <0, в P3(-1,-2) экстремума нет.
4) Для точки P4(-2,-1), Δ=144 – 36 >0, A<0 в P4(-2,-1) функция имеет максимум zmax=28
Пример №3. Найти наибольшее и наименьшее значения функции z = x2 + 4xy – y2 – 6x – 2y в треугольнике, ограниченном осями координат и прямой 2x + 3y – 6 = 0.
Решение.
Найдем критические точки локального экстремума внутри указанной области и значения данной функции z = f(x,y) в этих точках. Так как ![]() ,
,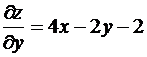 , то система для отыскания критических точек имеет вид
, то система для отыскания критических точек имеет вид
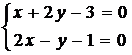 →
→ 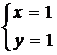 .
.
Точка P0(1;1) находится внутри области, причем z(P0) = -4. Исследуем функцию z на границе области. На отрезке ОА имеем : y=0, z = f(x;0) или g1(x)=x2 – 6x, где x∈[0;3]; g’1=2x-6; g’1(3)=0; g1(3)=f(3;0)=-9. На отрезке ОВ имеем: x=0. z=f(0;y) или z=g2(y)=-y2-2y, где y∈[0;2], g′2(y)=-2y-2, g′2(-1)=0, -1 ∉ [0;2]. На отрезке АВ имеем 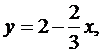
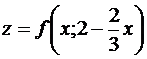 или
или
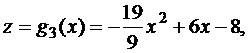 где x∈[0;3];
где x∈[0;3]; 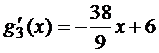 ;
; 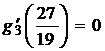 ,
,
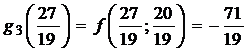 .
.
Найдем значения функции z в точках О, А и В. z(0) = f(0,0) = 0; z(A) = f(3;0) = -9, z(B) = f(0;2) = -8.
Сравнивая значения f(0;0), f(0;2), f(3;0), f(27/19;20/19), f(1;1), приходим к выводу:
наибольшее значение zmax=0 в т. O(0,0);
наименьшее значение zmin=-9 в т. A(3,0).
Задание №1. Исследовать на экстремум функцию двух переменных.
z = x2y2(1-x-y)
Решение.
1. Найдем частные производные.
![]()
![]()
2. Решим систему уравнений.
-x2·y2+2·x·y2(-x-y+1) = 0
-x2·y2+2·x2·y(-x-y+1) = 0
Получим:
а) Из первого уравнения выражаем x и подставляем во второе уравнение:
x1 = 0
x2 = -2/3·y+2/3
-y2(-2/3·y+2/3)2+2·y(-2/3·y+2/3)2(-1/3·y+1/3) = 0
Откуда, M1(2/3;0), M2(2/5;2/5), M3(0;1)
б) Из первого уравнения выражаем y и подставляем во второе уравнение: y = 0
y = -2/3·x+2/3
-x2(-2/3·x+2/3)2+2·x(-2/3·x+2/3)2(-1/3·x+1/3) = 0
Откуда, M4(0;2/3), M5(1;0)
Количество критических точек равно 5.
M1(2/3;0), M2(2/5;2/5), M3(0;1), M4(0;2/3), M5(1;0)
3. Найдем частные производные второго порядка.
![]()
![]()
![]()
4. Вычислим значение этих частных производных второго порядка в критических точках M(x0;y0).
Вычисляем значения для точки M1(2/3;0)
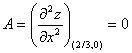
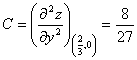
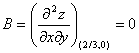
AC - B2 = 0, то вопрос о наличии экстремума остается открытым.
Вычисляем значения для точки M2(2/5;2/5)
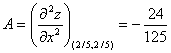
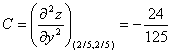
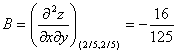
AC - B2 = 64/3125 > 0 и A < 0 , то в точке M2(2/5;2/5) имеется максимум z(2/5;2/5) = 16/3125
Вычисляем значения для точки M3(0;1)
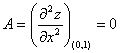
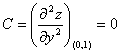
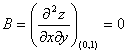
AC - B2 = 0, то вопрос о наличии экстремума остается открытым.
Вычисляем значения для точки M4(0;2/3)
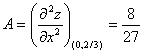
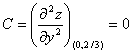
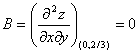
AC - B2 = 0, то вопрос о наличии экстремума остается открытым.
Вычисляем значения для точки M5(1;0)
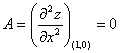
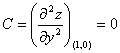
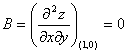
AC - B2 = 0, то вопрос о наличии экстремума остается открытым.
Вывод: В точке M2(2/5;2/5) имеется максимум z(2/5;2/5) = 16/3125;
Задание №2. Исследовать на экстремум z=3x+9y-x2-xy-y2-4.
