Определение точек локальных экстремумов функции многих переменных
Для функции f(x) многих переменных точка x представляет собой вектор, f’(x) − вектор первых производных(градиент) функции f(x), f ′ ′(x) − симметричную матрицу вторых частных производных(матрицу Гессе − гессиан) функции f(x).Для функции многих переменных условия оптимальности формулируются следующим образом.
Необходимое условие локальной оптимальности. Пусть f(x) дифференцируема в точке x*Rn. Если x* − точка локального экстремума, то f’(x*) = 0.
Как и ранее, точки, являющиеся решениями системы уравнений, называются стационарными. Характер стационарной точки x* связан со знакоопределенностью матрицы Гессе f′ ′(x).
Знакоопределенность матрицы А зависит от знаков квадратичной формы Q(α)=< α A, α > при всех ненулевых α∈Rn .
Здесь и далее через <x,y> обозначается скалярное произведение векторов x и y. По определению,
Матрица A является положительно(неотрицательно) определенной, если Q(α)>0 (Q(α)≥0) при всех ненулевых α∈Rn; отрицательно (неположительно) определенной, если Q(α)<0 (Q(α)≤0) при всех ненулевых α∈Rn; неопределенной, если Q(α)>0 для некоторых ненулевых α∈Rn и Q(α)<0 для остальных ненулевых α∈Rn.
Достаточное условие локальной оптимальности. Пусть f(x) дважды дифференцируема в точке x*Rn, причем f’(x*)=0 , т.е. x*− стационарная точка. Тогда, если матрица f′′(x*) является положительно (отрицательно) определенной, то x*− точка локального минимума (максимума); если матрица f′′(x*) является неопределенной, то x*− седловая точка.
Если матрица f′′(x*) является неотрицательно (неположительно) определенной, то для определения характера стационарной точки x* требуется исследование производных более высокого порядка.
Для проверки знакоопределенности матрицы, как правило, используется критерий Сильвестра. Согласно этому критерию, симметричная матрица А является положительно определенной в том и только том случае, если все ее угловые миноры положительны. При этом угловым минором матрицы А называется определитель матрицы, построенной из элементов матрицы А, стоящих на пересечении строк и столбцов с одинаковыми (причем первыми) номерами. Чтобы проверить симметричную матрицу А на отрицательную определенность, надо проверить матрицу (−А) на положительную определенность.
Итак, алгоритм определения точек локальных экстремумов функции многих переменных заключается в следующем.
1. Находится f′(x).
2. Решается система
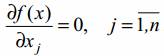
В результате вычисляются стационарные точки xi.
3. Находится f′′(x), полагается i=1.
4. Находится f′′(xi)
5. Вычисляются угловые миноры матрицы f′′(xi). Если не все угловые миноры ненулевые, то для определения характера стационарной точки xi требуется исследование производных более высокого порядка. При этом осуществляется переход к п.8.
В противном случае осуществляется переход к п.6.
6. Анализируются знаки угловых миноров f′′(xi). Если f′′(xi) является положительно определенной, то xi является точкой локального минимума. При этом осуществляется переход к п.8.
В противном случае осуществляется переход к п.7.
7. Вычисляются угловые миноры матрицы -f′′(xi) и анализируются их знаки.
Если -f′′(xi) − является положительно определенной, то f′′(xi) является отрицательно определенной и xi является точкой локального максимума.
В противном случае f′′(xi) является неопределенной и xi является седловой точкой.
8. Проверяется условие определения характера всех стационарных точек i=N.
Если оно выполняется, то вычисления завершаются.
Если условие не выполняется, то полагается i=i+1 и осуществляется переход к п.4.
Пример №1. Определить точки локальных экстремумов функции f(x) = x13 – 2x1x2 + x22 – 3x1 – 2x2




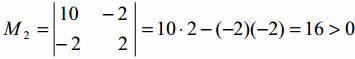
Поскольку матрица f′′(x2) является положительно определенной, то x2 является точкой локального минимума.
Ответ: функция f(x) = x13 – 2x1x2 + x22 – 3x1 – 2x2 имеет в точке x = (5/3; 8/3) локальный минимум.
Пример №2. Дана функция
f(x) = 2x12 + 4x1x23 – 10x1x2 + x22.
Требуется классифицировать точку х (0, 0)Т
Решение.
Вычисляем градиент функции Ñf(x).
∂f/∂x1 = 4x1 + 4x23 – 10x2
∂f/∂x2 = 12x1x22 – 10x1 +2x2
Ñf(x) = (0, 0)T,
следовательно, точка х – стационарная.
Вычисляем гессиан Hf(x):
∂2f/∂x12 = 4
∂2f/∂x22 = 24x1x2 + 2
∂2f/(∂x1∂x2) = 12x22 – 10, следовательно Hf(x) = Ñ2f(x) =![]()
Построим квадратичную форму:
xTHfx=(x1, x2)![]()
![]() =(4x1 –10x2, -10x1 + 2x2)
=(4x1 –10x2, -10x1 + 2x2)![]() =
=
= (4x1 – 10x2) x1 + (-10x1 + 2x2) x2 = 4x12 – 20x1x2 + 2x22
Если взять точку х = (0, 1)Т {x1=0; x2=1}; то xTHfx = 2 > 0.
Если взять точку х = (1, 1)Т {x1=1; x2=1}; то xTHfx = 4 – 20 + 2 = -14 < 0,т.е. Hf является неопределенной, поэтому точка х = (0, 0)Т представляет собой седловую точку.
