Уравнение прямой
Прямая, проходящая через две точки A1(x1; y1) и A2(x2; y2), представляется уравнением: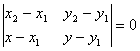
Оно выражает, что данные точки A1 и A2 лежат на одной прямой.
Уравнение можно представить в виде:
Инструкция. Для нахождения уравнения прямой, проходящей через две точки заполните координаты вершин, нажмите Далее. Полученное онлайн решение сохраняется в файле Word.
Пример. Составить уравнение прямой, проходящей через точки (1,5) и (3,9).
Решение. Формула (1) дает:
т.е. 2(y - 5) - 4(x - 1) = 0 или 2y - 4x - 6 = 0.
Формула (2) дает:
или
y = 2x + 3


