Действия над матрицами
Назначение сервиса. Матричный калькулятор предназначен для решения матричных выражений, например, таких как,3A-CB2 или A-1+BT.
Для выполнения списка операций используйте разделитель точка с запятой (;). Например, для выполнения трех операций:
а) 3А+4В
б) АВ-ВА
в) (А-В)-1
необходимо будет записать так:3*A+4*B;A*B-B*A;(A-B)^(-1)
Матрица - прямоугольная числовая таблица, имеющая m строк и n столбцов, поэтому схематически матрицу можно изображать в виде прямоугольника.
Нулевой матрицей (нуль-матрицей) называют матрицу, все элементы которой равны нулю и обозначают 0.
Единичной матрицей называется квадратная матрица вида
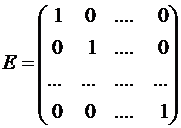
Две матрицы A и B равны, если они одинакового размера и их соответствующие элементы равны.
Вырожденной матрицей называется матрица, определитель которой равен нулю (Δ = 0).
Определим основные операции над матрицами.
Сложение матриц
Определение. Суммой двух матриц A=||aik|| и B=||bik|| одинакового размера называется матрица C=||cik|| тех же размеров, элементы которой находятся по формулеcik=aik+bik. Обозначается C=A+B.
.
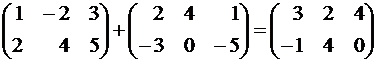A+0=A.
Еще раз подчеркнем, что складывать можно только матрицы одинакового размера; для матриц разных размеров операция сложения не определена.
Вычитание матриц
Определение. Разностью B-A матриц B и A одинакового размера называется такая матрица C, чтоA+C=B.
Умножение матриц
Определение. Произведением матрицы A=||aik|| на число α называется матрица C=||cik||, получающаяся из A умножением всех ее элементов на α, cik=α·aik.Определение. Пусть даны две матрицы A=||aik|| (i=1,2,...,m; k=1,2,...,n) и B=||bik|| (k=1,2,...,n; j=1,2,...,p), причем число столбцов A равно числу строк B. Произведением A на B называется матрица C=||cik||, элементы которой находятся по формуле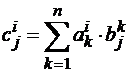 
.
Обозначается C=A·B.
Схематически операцию умножения матриц можно изобразить так:
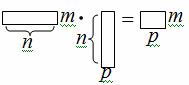
а правило вычисления элемента в произведении:
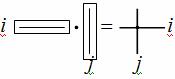
Подчеркнем еще раз, что произведение A·B имеет смысл тогда и только тогда, когда число столбцов первого сомножителя равно числу строк второго, при этом в произведении получается матрица, число строк которой равно числу строк первого сомножителя, а число столбцов равно числу столбцов второго. Проверить результат умножения можно через специальный онлайн-калькулятор.
Пример 7. Даны матрицы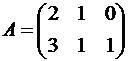 
и 
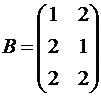. Найти матрицы C = A·B и D = B·A.
Решение. Прежде всего заметим, что произведение A·B существует, так как число столбцов A равно числу строк B.
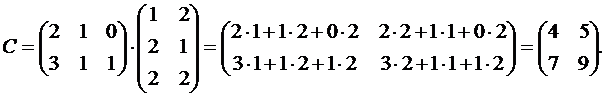
Заметим, что в общем случае
A·B≠B·A, т.е. произведение матриц антикоммутативно.
Найдем
B·A (умножение возможно).
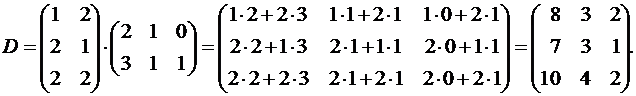
Пример 8. Дана матрица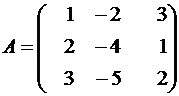 
. Найти 3A2 – 2A.
Решение.
.
; 
.
.
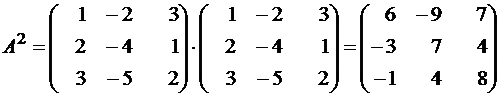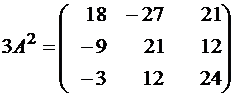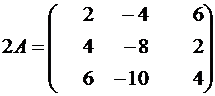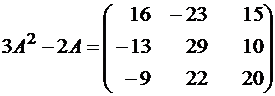Отметим следующий любопытный факт.
Как известно, произведение двух отличных от нуля чисел не равно нулю. Для матриц подобное обстоятельство может и не иметь места, то есть произведение ненулевых матриц может оказаться равным нуль-матрице.
Пример 9. Если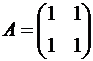 
и 
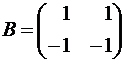, то
.
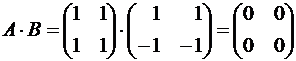Умножение матрицы на число
При умножении числа b матрицы A=(aij) получается матрица, элементы которой равны b·aij (каждый элемент матрицы умножается на число b).Подробнее о том, почему нельзя делить матрицы.
Пример 9. Найти значение многочлена f(x) от матрицы A, если f(x)=2x2–3x+5.
2*A^2-3*A+5*B
где A - матрица из задания, B = E - единичная матрица.
