Метод условного градиента
Назначение сервиса. Онлайн-калькулятор используется для нахождения минимума функции двух переменных f(x1,x2) методом условного градиента для случая линейных ограниченийax1+bx2 ≤ c.
Рассматривается ЗНП
f(x) → min, (1)
gi≤0, i=1,..,m, (2)
xi≥0, j=1,..,n, (3)
где f(x) - выпуклая функция.
Пусть x ∈ S - очередное приближение исходной задачи НП и ▽f(xk)≠0. Тогда в окрестности точки xk ЦФ f(x) представима в виде
fk(x)=▽fT(x-xk)
является приближением разности
Поставим вспомогательную задачу минимизации на множестве S линейной функции fk(x), т. е.
fk(x)=▽fT(x-xk) → min (4)
при тех же ограничениях (2), (3).
Пусть xk - решение этой задачи. Следующее приближение xk+1 к точке минимума x* исходной ЦФ f(x) на множестве S найдем по формуле:
xk+1=xk+αk(xk-xk), αk∈(0,1), (5)
В силу выпуклости S следует, что xk+1 ∈ S.
Величина αk из (5) может вычисляться различными способами. Например,
αk=min(1,α*k),
где α*k найдено из условия наискорейшего спуска по направлению
(xk-xk)=dk;
Другой способ вычисления значения αk. В начале выполнения итерации (5) полагают αk=1, после чего проверяют условие:
f(xk+1) < f(xk). (6)
Если это условие нарушается, то αk уменьшают в 2 раза (до тех пор, пока неравенство (6) не будет выполнено) и переходят к следующей итерации (5).
Критерий останова:
ǁ▽f(xk)ǁ≤ε или ǁxk-xk-1ǁ≤ε.
Отметим, что в общем случае задача (4) является задачей нелинейного программирования (gi(x) - нелинейные функции). Укажем случаи, когда поиск решения xk не представляет затруднений.
Допустимое множество S задано линейными ограничениями и условием неотрицательности переменных. Тогда (4) - ЗЛП и ее решение можно найти с помощью симплекс-метода.
Допустимое множество S={x∈Rn | aj≤xj≤bj, j=1,...,n} является n-мерным параллелепипедом. Тогда
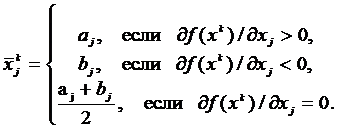 (7)
(7)
Пусть ▽f(xk)=g; ▽fT(xk)xk=d.
В этом случае имеем:
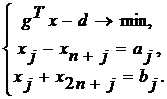
Имеем ЗЛП. Пусть n=2. Найдем начальную угловую точку. Имеем
x1-x3=b1; x2-x4=b2; x1+x5=a1; x2+x6=a2.
Составим таблицу.
Таблица 1
| x1 | x2 | x3 | x4 | x5 | x6 | |
| 1 | 0 | -1 | 0 | 0 | 0 | a1 |
| 0 | 1 | 0 | -1 | 0 | 0 | a2 |
| 1 | 0 | 0 | 0 | 1 | 0 | b1 |
| 0 | 1 | 0 | 0 | 0 | 1 | b2 |
Таблица 2
| x1 | x2 | x3 | x4 | x5 | x6 | |
| 1 | 0 | -1 | 0 | 0 | 0 | a1 |
| 0 | 1 | 0 | -1 | 0 | 0 | a2 |
| 0 | 0 | 1 | 0 | 1 | 0 | b1 – a1 |
| 0 | 0 | 0 | 1 | 0 | 1 | b2 – a2 |
Подставим в ЦФ это значение, получим: f(x)=g1x3+g2x4+p0,
где p0=g1b1+g2b2-d.
Если (g1, g2)>0, то в точке x0 достигнут минимум, т.е. x1*=a1, x2*=a2.
Если g1 или g2 < 0, то решаем задачу дальше. Составляем симплекс-таблицу.
Таблица 3
| x3 | x4 | ||
| x1 | -1 | 0 | a1 |
| x2 | 0 | -1 | a2 |
| x5 | 1 | 0 | b1 – a1 |
| x6 | 0 | 1 | b2 – a2 |
| g1 | g2 | - p0 |
Если g1 < 0, то разрешающим столбцом будет первый столбец. В этом столбце разрешающая строка третья. После преобразования получим
x1=a1+(b1-a1)=b1,
x1=b2.
Если g2<0, то аналогично получим:
x2=a2+(b2-a2)=b2.
Допустимое множество S={x∈Rn | ∑(xj-yj0)2≤R02}, то есть S - шар радиуса R0 с центром в точке y0. Тогда
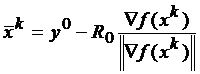 .
.
Пусть ▽f(xk)=g; ▽fT(xk)xk=d.
Тогда имеем следующую задачу
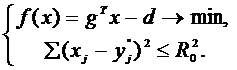
Составляем функцию Лагранжа L:
L=gTx-d+λ[∑(xj-y*j)2+y2-R02] → min .
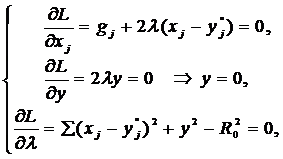
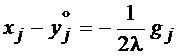 ;
; 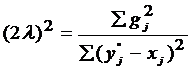 ;
;
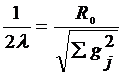 ;
; 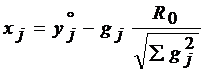
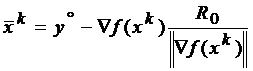 .
.
Пример. Решить ЗНП с помощью метода условного градиента, завершая вычисления при ǁxk-xk-1ǁ≤0.1.
f(x)=x12-4x1+x22-2x2 → min,
0≤x1≤1, 0≤x2≤2.
Решение. Возьмем x0=(0;0)∈S.
Шаг 1. Найдем ▽f=(2x1-4;2x2-2) в точке x0: ▽f(x0)=(-4;-2).
Запишем вспомогательную задачу (4):
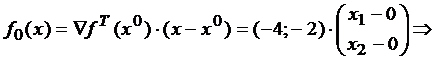
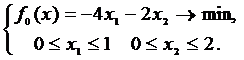
Это ЗЛП, ее можно решить симплекс-методом. Однако проще воспользоваться соотношениями (7), откуда следует: x0=(1;2).
Найдем α0 первым способом. В данном случае
F0(α) = f[x0+α·(x0-x0)] = f{(0;0)+α·[(1;2)-(0;0)]} = f(α, 2α) = 5α2-8α.
Из условия ▽F0(α)=0 ⇒ α=α*=0.8. Поэтому α0=min(1; 0.8)=0.8.
Вычислим очередное приближение x1 по формуле (5):
x1=(0;0)+0.8(1;2)=(0.8;1.6).
Т.к. ǁx0-x1ǁ=1.79>0.1=ε, то требуемая точность не достигнута.
Результаты вычислений на следующих итерациях приведены в таблице.
Таблица 4
| k | xk | ǁxk-xk-1ǁ | xk | αk |
| 1 | (0,8; 1,6) | 1,789 | (1; 0) | 0,8 |
| 2 | (0,892; 0,861) | 0,745 | (1; 2) | 0,212 |
| 8 | (0,957; 0,953) | 0,1 | Точность не достигнута | |
x*≈x8=(0.957;0.953); f*=f(x8)=-3.91.