Дробно-линейное программирование
Дробно-линейное программирование относится к нелинейному программированию, так как имеет целевую функцию, заданную в нелинейном виде.Задача дробно-линейного программирования в общем виде записывается следующим образом:
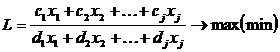
при ограничениях
a11x1+a12x2+...+a1jxj≤b1
a21x1+a22x2+...+a2jxj≤b2
... ... ... ... ... ... ... ... ...
am1x1+am2x2+...+amnxj≤bm
xj≥0; i=1,m; j=1,n
где сj,dj,bi,aij – постоянные коэффициенты.
d1x1+d2x2+...+dnxn ≠ 0
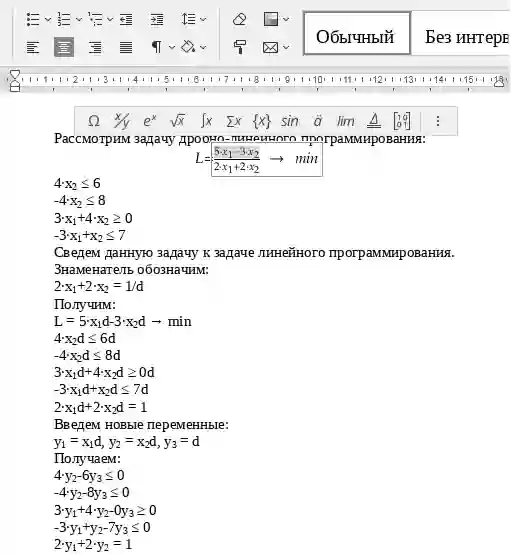
Рассмотрим задачу дробно-линейного программирования
![]()
при ограниченияхдробный линейный программирование
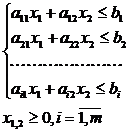
Будем считать, что
d1x1+d2x2 ≠ 0.
Математическая модель задачи дробно-линейного программирования может быть использована для определения рентабельности затрат на производство изделий, рентабельности продаж, затрат в расчете на рубль выпускаемой продукции, себестоимости изделий.
Пример №1. Для производства двух видов изделий A и В предприятие использует три типа технологического оборудования. Каждое из изделий должно пройти обработку на каждом из типов оборудования. Известно время обработки каждого из изделий и затраты, связанные с производством одного изделия.
| Тип оборудования | Затраты времени на обработку одного изделия, ч | |
| А | В | |
| I | 2 | 8 |
| II | 1 | 1 |
| III | 12 | 3 |
| Затраты на производство одного изделия, тыс. руб. | 2 | 3 |
Оборудование I и III типов предприятие может использовать не более 26 ч и 39 ч соответственно, оборудование II типа целесообразно использовать не менее 4 ч.
Определить, сколько изделий каждого вида следует изготовить предприятию, чтобы средняя себестоимость одного изделия была минимальной.
Решение. Составим математическую модель задачи. Пусть х1 – количество изделий видаА,которое следует изготовить предприятию,х2 –количество изделий видаВ.Общие затраты на их производство составят (2х1+3х2) тыс. руб., а средняя себестоимость одного изделия будет равна
Математическая модель задачи примет вид
![]()
при ограничениях
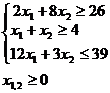 .
.
Задачу дробно-линейного программирования можно свести к задаче линейного программирования и решить симплексным методом.
Обозначим
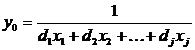
при условии d1·x1+d2·x2+ ... + dj·xj ≠ 0
и введем новые переменные yj=y0·xj. Тогда задача примет вид
L=c1·y1+c2·y2+ ... + cj·yj → max(min)
при ограничениях
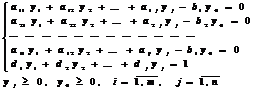
После нахождения оптимального решения полученной задачи, используя вышеуказанные соотношения, находят оптимальное решение исходной задачи дробно-линейного программирования.
Пример №2. Решить задачу дробно-линейного программирования симплексным методом.
![]()
при ограничениях
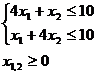 .
.
Решение. Сведем данную задачу к задаче линейного программирования. Сначала введем дополнительные переменные, чтобы привести задачу к каноническому виду:
![]()
при ограничениях
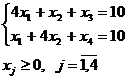 .
.
Обозначим ![]() , yj=y0·xj, j=1,4.
, yj=y0·xj, j=1,4.
Тогда задача принимает вид L=2y1+y2 → max
при ограничениях
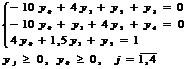 .
.
Решим полученную задачу симплекс-методом. Введем дополнительную переменную, чтобы получить единичный базис:
L=2y1+y2-Mz → max
при ограничениях
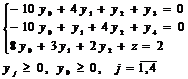 .
.
Составляем симплекс-таблицу.
| Базис | План | y0 | y1 | y2 | y3 | y4 | z |
| y3 | 0 | -10 | 4 | 1 | 1 | 0 | 0 |
| y4 | 0 | -10 | 1 | 4 | 0 | 1 | 0 |
| z | 2 | 8 | 3 | 2 | 0 | 0 | 1 |
| L | -2M | -8M | -3M-2 | -2M-1 | 0 | 0 | 0 |
В последней оценочной строке есть отрицательные оценки, поэтому нужно делать шаг симплекс-метода. Выбираем столбец с наименьшей оценкой, а затем разрешающий элемент – по наименьшему отношению свободных членов к коэффициентам столбца. Результат шага запишем в таблицу. Аналогично будем повторять шаги.
| Базис | План | y0 | y1 | y2 | y3 | y4 | z |
| y3 | 5/2 | 0 | 31/4 | 7/2 | 1 | 0 | 5/4 |
| y4 | 5/2 | 0 | 19/4 | 13/2 | 0 | 1 | 5/4 |
| y0 | 1/4 | 1 | 3/8 | 1/4 | 0 | 0 | 1/8 |
| L | 0 | 0 | -2 | -1 | 0 | 0 | M |
| Базис | План | y0 | y1 | y2 | y3 | y4 | z |
| y1 | 10/31 | 0 | 1 | 14/31 | 4/31 | 0 | 5/31 |
| y4 | 30/31 | 0 | 0 | 135/31 | -19/31 | 1 | 15/31 |
| y0 | 4/31 | 1 | 0 | 5/62 | -3/62 | 0 | 2/31 |
| L | 20/31 | 0 | 0 | -3/31 | 8/31 | 0 | M+10/31 |
| Базис | План | y0 | y1 | y2 | y3 | y4 | z |
| y1 | 2/9 | 0 | 1 | 0 | 26/135 | -14/135 | 1/9 |
| y2 | 2/9 | 0 | 0 | 1 | -19/135 | 31/135 | 1/9 |
| y0 | 1/92/3 | 1 | 0 | 0 | -1/27 | -1/54 | 1/18 |
| L | 0 | 0 | 0 | 11/45 | 1/45 | M+1/3 |
Получили решение
Тогда, возвращаясь к исходным переменным, получим:
Пример №3. Рассмотрим следующую задачу.
Завод выпускает продукцию n видов p1,…,pn. В процессе производства используются m видов сырья S1,…,Sm, запасы которого ограничены. Требуется составить производственный план таким образом, чтобы обеспечить максимально возможную рентабельность работы заводов. Нормы расхода сырья, его запасы, а также удельные и условно постоянные затраты и прибыль, получаемая заводом от реализации одного изделия, приведены в таблице 2.
Таблица 2 - Исходные данные
| Сырье | Продукция | Запасы | ||||
| p1 | . . . | pj | . . . | pn | сырья | |
| S1 | a11 | . . . | a1j | . . . | a1n | b1 |
| … | . . . | . . . | . . . | . . . | . . . | . . . |
| Si | ai1 | . . . | aij | . . . | ain | bi |
| … | . . . | . . . | . . . | . . . | . . . | |
| Sm | am1 | . . . | amj | . . . | amn | bm |
Удельные затраты на 1 изделие | d1 | . . . | dj | . . . | dn | Условно-постоянные затраты
d0 |
Прибыль от реализации изделия | c1 | . . . | cj | . . . | cn | |
Определения:
1. Рентабельность – показатель, представляющий собой отношение прибыли к сумме затрат на производство (%).
2. Условно-переменные (удельные) затраты – затраты, которые изменяются прямо пропорционально объемам выпуска товаров (затраты на материалы, энергию, комплектующие, зарплату).
3. Условно-постоянные затраты – затраты, которые практически не зависят от изменения количества выпускаемой продукции (затраты на освещение, арендная плата и др.).
Пусть x1,..,xn– объем выпуска продукции p1,…,pn Математическая модель будет иметь вид:
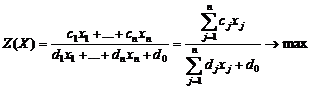
xj≥0, j=1,n
Сведем данную задачу к задаче линейного программирования. Обозначим через 1/δ знаменатель целевой функции, δ>0.
Умножим правую и левую части ограничения модели на δ Получим
xj≥0, δ>0, j=1,n
Обозначим yj=xj·δ. Получим модель линейного программирования с переменными xj, j=1,n и δ.
∑dj·yj+d0·δ=1
yj≥0, j=1,n, δ>0.
Пример №4.
![]()
18x1+0.2x2≤20 (*)
2.55x1+1.2x2≤45 (**)
x1, x2≥0
Решение.
0.01x1+0.04x2+1=1/δ
Z=0.012x1δ+0.008x2δ → max
18x1δ+0.2x2δ≤20δ
2.55x1δ+1.2x2δ≤45δ
0.01x1δ+0.04x2δ+δ=1
x1≥0, x2≥0, δ>0
y1=x1δ, y2=x2δ
18y1+0.2y2-20δ≤0
2.55y1+1.2y2-45δ≤0
0.01y1+0.04y2+δ=1
y1≥0, y2≥0, δ>0
Решаем симплекс-методом. Получим
y1=5, y2=10, z=14%.
δ=1-0.01y1-0.04y2 = 0.55
Тогда x1=5/0.55 = 9.09, x2=10/0.55 = 18.18.
Графическое решение задачи приведено на рис. 1.
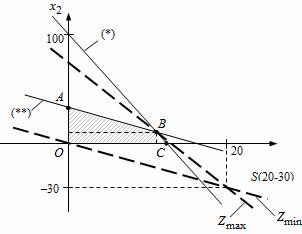
Рис. 1- Геометрическая интерпретация задачи
Ограничения задачи – это множество допустимых решений, лежащих в четырехугольнике АВСО. Целевая функция задачи – линии уровня цели, проходящие через точку S. Координаты точки S определяются в результате решения системы уравнений:
(числитель целевой функции);
0.012x1+0.008x2=0
0.01x1+0.04x2+1=0
(знаменатель целевой функции).