Формулировка основных типов задач ЛП, построение их математических моделей
Задачи, решаемые методами ЛП, очень разнообразны по содержанию. Но их математические модели схожи и условно объединяются в три большие группы задач:- транспортные задачи;
- задачи о составлении плана;
- задачи о смеси (о диете).
Транспортная задача
На двух торговых базах А и В имеется 30 гарнитуров мебели, по 15 на каждой. Всю мебель требуется доставить в два мебельных магазина, С и Д причем в С надо доставить 10 гарнитуров, а в Д - 20. Известно, что доставка одного гарнитура с базы А в магазин С обходится в одну денежную единицу, в магазин Д - в три денежных единицы. Соответственно с базы В в магазины С и Д: две и пять денежных единиц. Составить план перевозок так, чтобы стоимость всех перевозок была наименьшей.Данные задачи для удобства разметим в таблице. На пересечении строк и столбцов стоят числа, характеризующие стоимость соответствующих перевозок (табл. 3.1).
Таблица 3.1
| магазины / базы | С | Д | отправлено гарнитуров |
| А | 1 | 3 | 15 |
| В | 2 | 5 | 15 |
| получено гарнитуров | 10 | 20 | 30 = 30 |
Составим математическую модель задачи.
Необходимо ввести переменные. В формулировке вопроса говорится, что необходимо составить план перевозок. Обозначим через х1, х2 количество гарнитуров, перевозимых с базы А в магазины С и Д соответственно, а через у1, у2 - количество гарнитуров, перевозимых с базы В в магазины С и Д соответственно. Тогда количество мебели, вывозимое со склада А, равно (х1 + х2), а со склада В - (у1 + у2). Потребность магазина С равна 10 гарнитурам, и в него привезли (х1 + у1) штук, т. е. х1 + у1 = 10. Аналогично, для магазина Д имеем х2 + у2 = 20. Заметим, что потребности магазинов в точности равны количеству гарнитуров, имеющихся на складах, поэтому х1 + у2 = 15 и у1 + у2 = 15. Если бы со складов вы увезли меньше, чем по 15 комплектов, то магазинам не хватило бы мебели для удовлетворения их потребностей.
Итак, переменные х1, х2, у1, у2 по смыслу задачи неотрицательны и удовлетворяют системе ограничений:
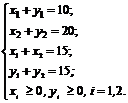 (3.1)
(3.1)
Обозначив через F транспортные расходы, посчитаем их. на перевозку одного комплекта мебели из А в С тратится одна ден. ед., на перевозку x1 комплектов - x1 ден. ед. Аналогично, на перевозку x2 комплектов из А в Д затратится 3x2 ден. ед.; из В в С - 2y1 ден. ед., из В в Д - 5y2 ден. ед.
Итак,
F = 1x1 + 3x2 + 2y1 + 5y2 → min (3.2)
(мы хотим, чтобы общая стоимость перевозок была минимальной).
Сформулируем задачу математически.
На множестве решений системы ограничений (3.1) найти такое решение, которое обращает в минимум целевую функцию F (3.2), или найти оптимальный план (x1, x2, y1, y2), определяемый системой ограничений (3.1) и целевой функцией (3.2).
Задача, которую мы рассмотрели может быть представлена в более общем виде, с любым числом поставщиков и потребителей.
В рассмотренной нами задаче наличие груза у поставщиков (15 + 15) равно общей потребности потребителей (10 + 20). Такая модель называется закрытой, а соответствующая задача - сбалансированной транспортной задачей.
В экономических расчетах немалую роль играют и так называемые открытые модели, в которых указанное равенство не соблюдается. Либо запас у поставщиков больше потребности у потребителей, либо спрос превышает наличие товара. заметим, что тогда в систему ограничений несбалансированной транспортной задачи наряду с уравнениями будут входить и неравенства.
Перейти к онлайн решению своей задачи
Рассмотрим пример несбалансированной транспортной задачи.
В пунктах А и В расположены кирпичные заводы, а в С и Д - карьеры, снабжающие их песком. потребность заводов в песке меньше, чем производительность карьеров. Известно, сколько песка нужно каждому из заводов и сколько добывается в каждом карьере. Также известна стоимость перевозки 1 т песка из каждого карьера к заводам (числа на стрелочках). Нужно так спланировать снабжение заводов песком, чтобы затраты на перевозку были наименьшими. Данные задачи на схеме.
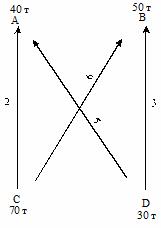
Постоим математическую модель задачи.
Введем переменные:
x11 - количество тонн песка, перевозимого с карьера С на завод А;
x12 - с карьера С на завод А;
x21 - количество тонн песка в А с карьера Д;
x22 - количество тонн песка с карьера Д на завод В.
На завод А должно быть доставлено 40 т с обоих карьеров, значит x11 + x21 = 40, на завод В должно быть доставлено 50 т, значит x12 + x22 = 50. Из карьера С вывезено не более 70 т, т. е. x11 + x12 ≤ 70, аналогично x21 + x22 ≤ 30. Имеем систему ограничений:
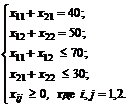 (3.3)
(3.3)
И целевая функция F, выражающая стоимость перевозок, имеет вид
F= 2x11 + 6x12 + 5x21 + 3x22→min. (3.4)
Задача о составлении плана
Некоторому заводу требуется составить оптимальный план выпуска двух видов изделий, которые обрабатываются на четырех видах машин. Известны определенные возможности и производительность оборудования; цена изделий, обеспечивающая прибыль заводу, составляет 4 тыс. руб. за изделие I вида, 6 тыс. руб. - за изделие II вида. Составить план выпуска этих изделий так, чтобы от реализации их завод получил наибольшую прибыль. В таблице указано время, необходимое для обработки каждого из двух видов изделий на оборудовании всех четырех видов (табл. 3.2).Таблица 3.2
Изделия |
Виды машин | |||
| 1 | 2 | 3 | 4 | |
| I | 1 | 0,5 | 1 | 0 |
| II | 1 | 1 | 0 | 1 |
| Возможное время работы машин | 18 | 12 | 12 | 9 |
Построим математическую модель.
В задаче необходимо определить план выпуска изделий, обозначим за x количество изделий I вида, за y - количество изделий II вида. Тогда посчитаем, сколько времени затратит первая машина на обработку всех производственных изделий. Она тратит одну единицу времени на одного изделие I вида, значит на x штук изделий потратит 1x ед. времени, на обработку y изделий II вида затратится 1y ед. времени. Всего резерв времени работы первой машины - 18 единиц времени. Значит, x + y ≤ 18. Аналогичные рассуждения со второй машиной, третьей и четвертой дадут систему ограничений:
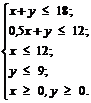 (3.5)
(3.5)
Общая прибыль будет выражена в целевой функции:
F = 4x + 6y → max. (3.6)
Задача состоит в нахождении на множестве решений системы (3.5) такого решения, при котором значение целевой функции (3.6) было бы максимальным.
Задача составления смеси
Еще одна распространенная задача ЛП - задача о составлении смеси. Примером таких задач может быть задача о составлении таких смесей нефтепродуктов, которые бы удовлетворяли определенным техническим требованиям и были наиболее дешевыми по стоимости. Либо задачи о рационе, когда известна потребность в определенных веществах и содержание этих веществ в различных продуктах. Необходимо составить рацион так, чтобы удовлетворить потребности в необходимых веществах и при этом продуктовая корзина имела бы минимальную стоимость при заданных ценах на продукты.Практически подобные задачи ставятся, к примеру, в любом животноводческом хозяйстве и имеют очень большой спектр применения.
Рассмотрим пример. Для откорма цыплят на птицефабрике в их рацион необходимо включать не менее 33 единиц вещества А, 23 единиц питательного вещества В, 12 единиц С. Для откорма используются три вида корма. Данные о содержании питательных веществ в каждом виде корма заданы таблицей. Также известна стоимость кормов. Необходимо составить наиболее дешевый рацион (табл. 3.3).
Таблица 3.3
| Корма-продукты | Вещества | Стоимость 1 ед. корма | ||
| А | В | С | ||
| I | 4 | 3 | 1 | 20 |
| II | 3 | 2 | 1 | 20 |
| III | 2 | 1 | 2 | 10 |
Для понимания задачи можете представить себе, что вещества А, В, С - это жиры, белки, углеводы, а продукты I, II, III - то, чем кормят цыплят, например пшено, комбикорм, витаминные добавки. Тогда первая строка таблицы показывает содержание в одной единице пшена: 4 ед. белка, 3 ед. жиров, одной ед. углеводов. Вторая строка - содержание белков, жиров, углеводов в 1 ед. II продукта и т. д.
Если постановка задачи ясна, приступим к построению математической модели.
В качестве ответа на поставленную задачу мы должны предложить рацион, т. е. указать сколько и каких кормов взять, чтобы необходимое количество питательных веществ было соблюдено и при этом он стоил как можно дешевле.
Поэтому, обозначим за x1 количество кормов типа I в рационе, за x2 - количество кормов типа II и, соответственно, x3 - количество корма III в рационе. Тогда, вещества А при употреблении такого рациона цыплята получат 4x1 - при потреблении продуктов типа I, 3x2 - при потреблении II продукта, 2x3 - при потреблении III. Всего вещества А необходимо употребить по условию задачи не менее 33 единиц, следовательно 4x1 + 3x2 + 2x3 ≥ 33.
Аналогично рассуждая с веществами В и С, имеем:
3x1 + 2x2 + 1x3 ≥ 23 и x1 + x2 + 2x3 ≥ 12.
Таким образом, получим систему ограничений:
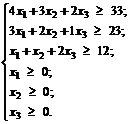 (3.7)
(3.7)
Переменные неотрицательны по смыслу задачи. При этом стоимость рациона выражается функцией:
F = 20x1 + 20x2 + 10x3 → min, (3.8)
т. к. 20, 20, 10 - стоимость одной ед. продуктов I, II, III типов соответственно, а в рационе их содержится x1, x2, x3 единиц.
Система ограничений (3.7) вместе с целевой функцией (3.8) и составляют математическую модель исходной задачи. Решить ее - значит найти x1, x2, x3, удовлетворяющие системе ограничений и обращающие значение функции F в минимальное.
Расстановка типов судов по линиям
Построить такой план расстановки двух типов судов по трем линиям, который обеспечил бы максимум суммарной провозной способности флота, но не меньше заданного на линиях объема перевозок.| Тип судна | Производительность судов, млн. тонно-миль в сутки | Эксплуатационный период, сутки | ||
| 1-я линия | 2-я линия | 3-я линия | ||
| 1 | p11 | p12 | p13 | s1 |
| 2 | p21 | p22 | p23 | s2 |
| Заданный объем перевозки, млн. тонно-миль | V1 | V2 | V3 | |
Экономико-математическая модель задачи.
Ограничения по эксплуатационному периоду:
x1/p11+ x2/p12+ x3/p13 ≤ s1
x4/p21+ x5/p22+ x6/p23 ≤ s2
Ограничения по поставкам:
s1x1+ s2x4 ≥ V1
s1x2+ s2x5 ≥ V2
s1x3+ s2x6 ≥ V3
Целевая функция
p11x1+p12x2+p13x3+p21x4+p22x5 +p23x6 → max
Построение математической модели для симплекс-задачи
Вопросы для самоконтроля
1. Постановка транспортной задачи. опишите построение математической модели.
2. Что такое сбалансированная и несбалансированная транспортная задача?
3. Что подсчитывается в целевой функции транспортной задачи?
4. Что отражает каждое неравенство системы ограничений задачи о плане?
5. Что отражает каждое неравенство системы ограничений задачи о смеси?
6. Что обозначают переменные в задаче о плане и задаче о смеси?
