Симплекс-метод в строчечной форме записи. Пример решения
Примечание: существуют и другие формы записи симплекс-метода.Рассмотрим пример решения прямой задачи линейного программирования строчечным симплекс-методом через калькулятор.
Определим максимальное значение целевой функции F(X) = 3x1+5x2+4x3 при следующих условиях-ограничений.
0.1x1+0.2x2+0.4x3≤1100
0.05x1+0.02x2+0.02x3≤120
3x1+x2+2x3≤8000
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
0.1x1 + 0.2x2 + 0.4x3 + 1x4 + 0x5 + 0x6 = 1100
0.05x1 + 0.02x2 + 0.02x3 + 0x4 + 1x5 + 0x6 = 120
3x1 + 1x2 + 2x3 + 0x4 + 0x5 + 1x6 = 8000
В качестве начальной допустимой базы можно взять B0 = <4, 5, 6>. Ей будет соответствовать следующая таблица.
| 1100 | 0.1 | 0.2 | 0.4 | 1 | 0 | 0 |
| 120 | 0.05 | 0.02 | 0.02 | 0 | 1 | 0 |
| 8000 | 3 | 1 | 2 | 0 | 0 | 1 |
| 0 | -3 | -5 | -4 | 0 | 0 | 0 |
Поскольку задача решается на максимум, то ведущий столбец выбирают по минимальному отрицательному числу в последней строке.
| 1100 | 0.1 | 0.2 | 0.4 | 1 | 0 | 0 |
| 120 | 0.05 | 0.02 | 0.02 | 0 | 1 | 0 |
| 8000 | 3 | 1 | 2 | 0 | 0 | 1 |
| 0 | -3 | -5 | -4 | 0 | 0 | 0 |
Вычислим значения Di по строкам как частное от деления:
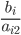и из них выберем наименьшее:
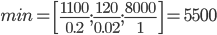
Следовательно, 1-ая строка является ведущей. Вместо переменной x4 в план войдет переменная x2. Разделим 1-ую строку на 0.2 и прибавим к последней строке, а затем вычтем из всех остальных строк.
Представим расчет каждого элемента в виде таблицы:
| B | x1 | x2 | x3 | x4 | x5 | x6 |
| 1100 / 0.2 = 5500 | 0.1 / 0.2 = 0.5 | 0.2 / 0.2 = 1 | 0.4 / 0.2 = 2 | 1 / 0.2 = 5 | 0 / 0.2 = 0 | 0 / 0.2 = 0 |
 |  |  |  |  |  |  |
|  |
|  |
|  |
|
 |  |  |  |  |  | |
| 5500 | 0.5 | 1 | 2 | 5 | 0 | 0 |
| 10 | 0.04 | 0 | -0.02 | -0.1 | 1 | 0 |
| 2500 | 2.5 | 0 | 0 | -5 | 0 | 1 |
| 27500 | -0.5 | 0 | 6 | 25 | 0 | 0 |
Вычислим значения Diпо строкам как частное от деления:
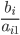и из них выберем наименьшее:
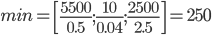
Следовательно, 2-ая строка является ведущей. Вместо переменной x5в план войдет переменная x1. Разделим 2-ую строку на 0.04 и прибавим к последней строке, а затем вычтем из всех остальных строк.
Представим расчет каждого элемента в виде таблицы:
| B | x1 | x2 | x3 | x4 | x5 | x6 |
|  |
|  |
|  |
|
| 10 / 0.04 = 250 | 0.04 / 0.04 = 1 | 0 / 0.04 = 0 | -0.02 / 0.04 = -0.5 | -0.1 / 0.04 = -2.5 | 1 / 0.04 = 25 | 0 / 0.04 = 0 |
|  |
|  |
|  |
|
 |  |  |  |  |  | |
Последняя строка не содержит отрицательных элементов. Найден оптимальный план.
Окончательный вариант таблицы:
| 5375 | 0 | 1 | 2.25 | 6.25 | -12.5 | 0 |
| 250 | 1 | 0 | -0.5 | -2.5 | 25 | 0 |
| 1875 | 0 | 0 | 1.25 | 1.25 | -62.5 | 1 |
| 27625 | 0 | 0 | 5.75 | 23.75 | 12.5 | 0 |
Примечание:
1. Число операций в симплекс-методе не превосходит n!/((n-m)!*m!)
2. Решение х системы уравнений, в котором все небазисные переменные равны 0, называется базисным решение.
3. Если все компоненты базисного решения неотрицательны, то оно называется допустимым базисным решение или опорным планом.
Пример. Собственник располагает четырьмя видами ресурсов. Это, например, денежные средства, производственные помещения, оборудование, сырье. Ресурсы необходимо распределить между шестью видами предприятий. Предприятия различаются по экономическим условиям деятельности: месту расположения, системе налогообложения, стоимости электроэнергии, оплате труда и т. д., в связи , с чем имеют разные издержки производства. Относительные уровни издержек заданы в таблице.
Распределение ресурсов по предприятиям сопряжено с необходимостью ряда ограничений, которые могут быть описаны системой четырех уравнений с шестью неизвестными.
Смысл первого уравнений в нашем примере в том, что ресурс вида 1, общий ресурс которого составляет 16 единиц, может размещаться в количестве четырех единиц на предприятии первого типа и одной единицы – на предприятии четвертого типа. Аналогично раскрывается смысл второго и последующих уравнений. Последнее условие говорит о том, что число предприятий не может быть отрицательным.
Необходимо определить, какое количество предприятий каждого типа следует иметь, чтобы общие издержки были минимальными.
