Уравнение нормали к графику функции
Уравнение нормали в общем виде записывается как: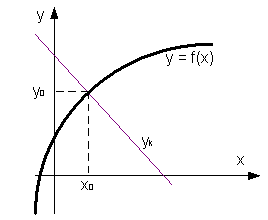
(x–x0)x’+(y-y0)y’=0
Назначение сервиса. Данный сервис предназначен для нахождения уравнения нормали к кривой. Решение оформляется в формате Word. Для получения уравнения необходимо выбрать вид заданной функции.
Алгоритм составления уравнения нормали к графику функции
- Вычисление значения функции y0 в точке x0:y0 = f(x0). Если исходное значение y0 задано, то переходим к п.2.
- Нахождение производной y'(x).
- Вычисление значения производной при x0.
- Запись уравнения нормали к кривой линии в форме: yk = y0 - 1/y'(y0)(x - x0)
Пример
Задание №1
Найти уравнение нормали к параболе y = 1/2*x2 в точке (-2;2).
Решение находим с помощью калькулятора.
Запишем уравнения нормали в общем виде:
![]()
По условию задачи x0 = -2, тогда y0 = 2
Теперь найдем производную:
y' = (1/2•x2)' = x
следовательно:
f'(-2) = -2 = -2
В результате имеем:
![]()
или
yk = 1/2•x+3
Задание №2
Написать уравнения нормали к кривой y2-1/2*x3-8 в точке M0(0;2).
Решение.
Поскольку функция задана в неявном виде, то производную ищем по формуле:
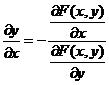
Для нашей функции:
![]()
![]()
Тогда:
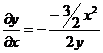
или
![]()
следовательно:
Fx'(0;2) = 3/4•02/2 = 0
В результате имеем:
![]()
или
x = 0
Задание №3
Написать уравнения нормали к эллипсу, заданному в параметрической форме: x = 5*sqrt(2)*cos(t);y = 3*sqrt(2)*sin(t) в точке M0(-5;3).
Решение.
Запишем уравнения нормали в для функции, заданной в параметрической форме:
(x - x0)x' + (y - y0)y' = 0
Данной точке M0(-5;3) соответствует значение t = 3/4•π
Для нашей функции:
![]()
![]()
следовательно:
(x +5)-5 + (y - 3)-3 = 0
или
yk = -5x-3y-16
