Графический метод решения задач линейного программирования с помощью таблиц Excel
Постановка задачиНайти графическим методом максимум целевой функции
F=2x1+3x2 → max
x1+3x2≤18, (1)
2x1+x2≤16, (2)
x2≤5, (3)
3x1≤21, (4)
x1≥0, x2≥0, (5,6)
при ограничениях
Решение с помощью таблиц Excel
Вначале построим на листе Excel решение системы неравенств.
Рассмотрим первое неравенство x1+3x2≤18.
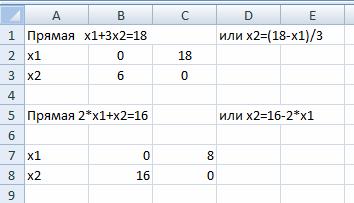
Построим граничную прямую x1+3x2=18 по двум точкам. Прямую обозначим (L1)(или Ряд1). Координаты х2 считаем по формулам:
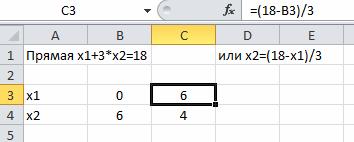
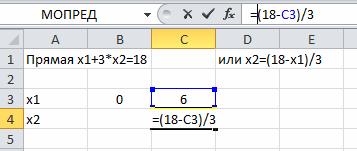
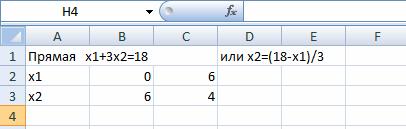
Для построения выбираем точечную диаграмму
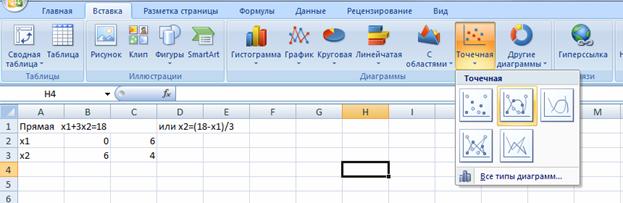
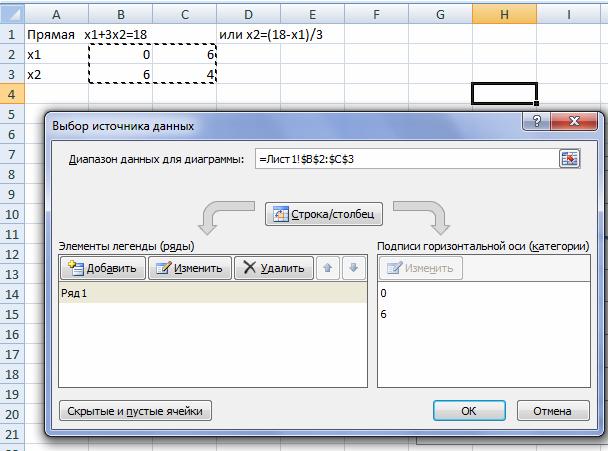
Выбираем данные для прямой
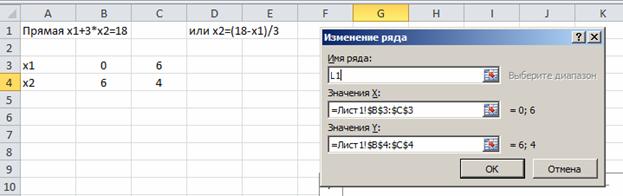
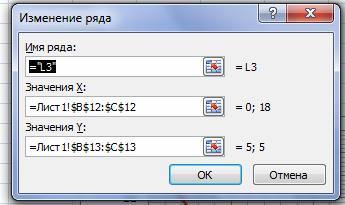
Изменяем название прямой:
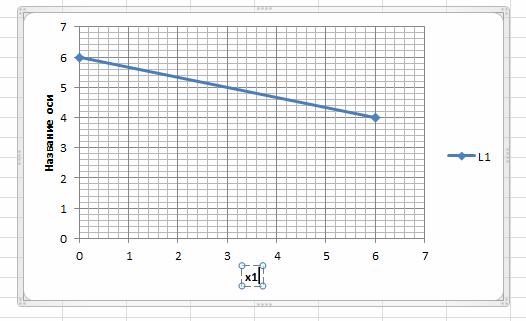
Выбираем макет диаграммы. Изменяем название осей координат:
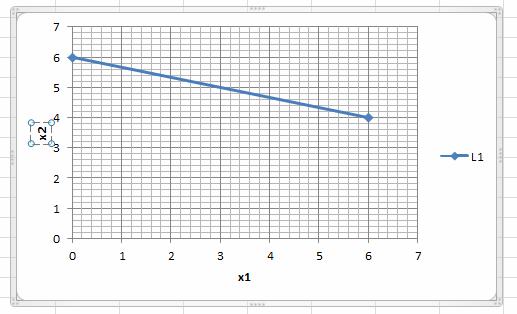
Прямая (L1) на графике:
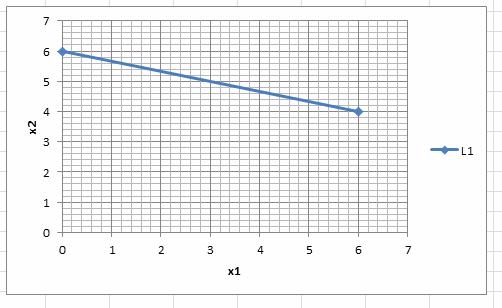
Решение строгого неравенства x1+3x2≤18 можно найти с помощью единственной пробной точки, не принадлежащей прямой (L1). Например, с помощью точки (0; 0)Ï(L1).
При подстановке координат точки (0; 0), получаем неравенство
0 + 3×0 < 18 или 0 < 18 .
Неравенство является верным, следовательно решением неравенства (1) будет та полуплоскость, в которой пробная точка расположена (на рисунке ниже прямой L1).
Затем решаем неравенство (2) 2x1+x2≤16.
Построим граничную прямую 2x1+x2=16 по двум точкам. Прямую обозначим (L2).
Прямая (L2) на графике:
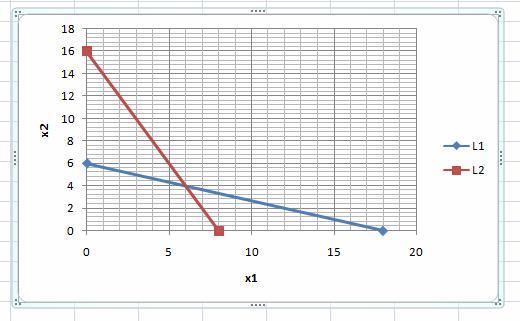
Решение строгого неравенства 2x1+x2≤16 можно найти с помощью единственной пробной точки, не принадлежащей прямой (L2). Например, с помощью точки (0; 0)Ï(L2).
При подстановке координат точки (0; 0), получаем неравенство
2×0 + 0 < 16 или 0 < 16 .
Неравенство является верным, следовательно решением неравенства (2) будет та полуплоскость, в которой пробная точка расположена (на рисунке ниже прямой L2).
Затем решаем неравенство (3) x2≤5.
Построим граничную прямую x2=5 по двум точкам. Прямую обозначим (L3).
На листе Excel добавляем данные
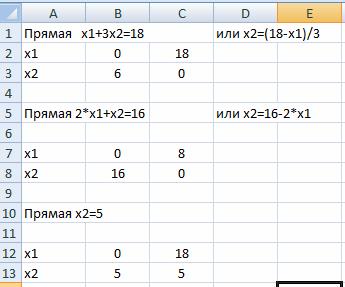
Прямая (L3) на графике:
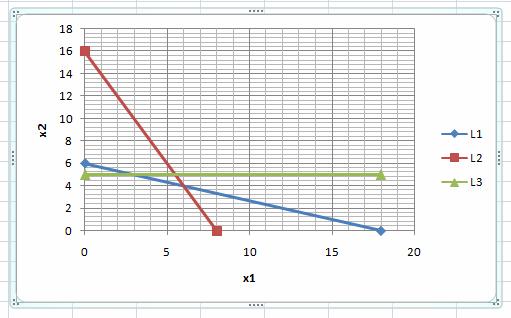
Решение строгого неравенства 2x2<5 можно найти с помощью единственной пробной точки, не принадлежащей прямой (L3). Например, с помощью точки (0; 0)Ï(L3).
При подстановке координат точки (0; 0), получаем неравенство
0 < 5 .
Неравенство является верным, следовательно решением неравенства (3) будет та полуплоскость, в которой пробная точка расположена (на рисунке ниже прямой L3).
Затем решаем неравенство (4) 3x2≤21.
Построим граничную прямую 3x2=21 по двум точкам. Прямую обозначим (L4).
На листе Excel добавляем данные
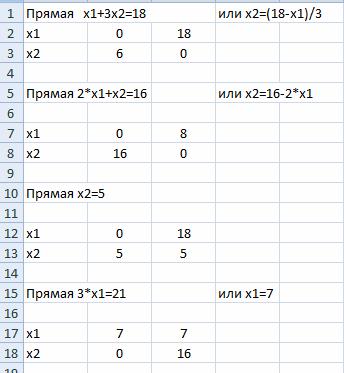
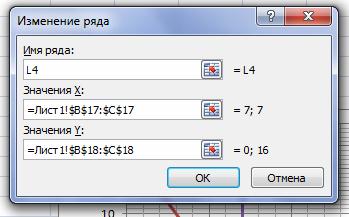
Прямая (L4) на графике:
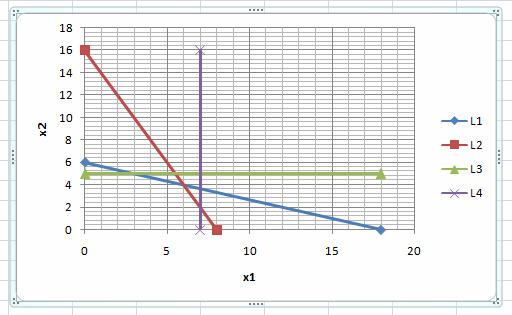
Решение строгого неравенства 3х1 < 21 можно найти с помощью единственной пробной точки, не принадлежащей прямой (L4). Например, с помощью точки (0; 0)Ï(L4).
При подстановке координат точки (0; 0), получаем неравенство
0 < 21 .
Неравенство является верным, следовательно, решением неравенства (4) будет та полуплоскость, в которой пробная точка расположена (на рисунке левее прямой L4).
Решением двух неравенств (5) и (6) x1≥0 и x2≥0 является 1-ая четверть, ограниченная координатными прямыми x1=0 и x2=0.
Система неравенств решена. Решением системы неравенств (1) – (6) в данном примере является выпуклый многоугольник в левом нижнем углу рисунка, ограниченный прямыми L1, L2, L3, L4 и координатными прямыми x1=0 и x2=0. Убедиться, что многоугольник выбран правильно, можно подстановкой пробной точки, например (1; 1) в каждое неравенство исходной системы. При подстановке точки (1; 1) получаем, что все неравенства, в том числе естественные ограничения, верные.
Рассмотрим теперь целевую функцию
F = 2x1 + 3x2.
Построим линии уровня для значений функции F = 0 и F = 12 (числовые значения выбраны произвольно). На листе Excel добавляем данные

Линии уровней на графике:
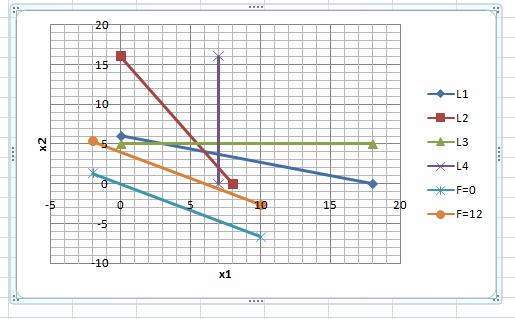
Построим вектор направлений (или градиент) {2; 3}. Координаты вектора совпадают с коэффициентами целевой функции F.
Добавляем на листе Excel координаты начальной и конечной точки вектора.
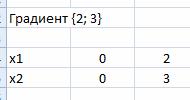
Вектор на рисунке:
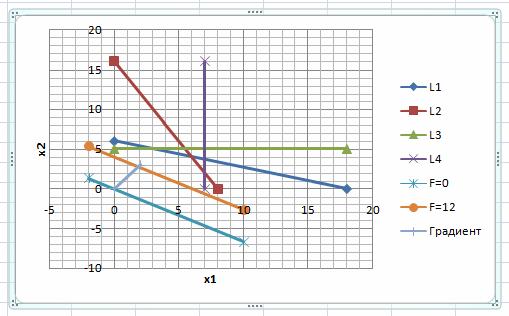
Градиент указывает направление увеличения целевой функции F.
Теперь следует линию уровня F=0 передвинуть параллельно до последней точки угловой точки выпуклого многоугольника. Последней угловой точкой пересечения выпуклого многоугольника и передвинутой линии уровня будет точка пересечения прямых L1 и L2. Для нахождения координат точки решим систему уравнений
x1+3x2=18
2x1+x2=16
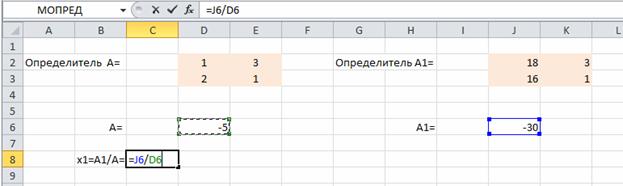
Решаем систему уравнений по формулам Крамера. Для этого на листе Excel создаем массивы для определителей. Для вычисления определителей используем математическую функцию МОПРЕД
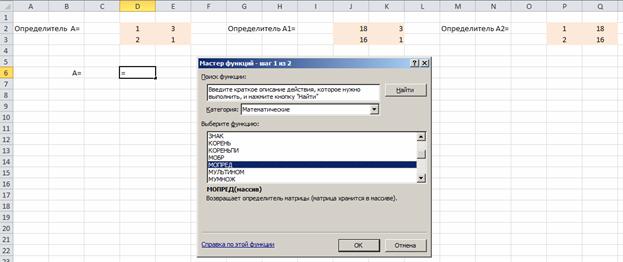
Выделяем массив определителя
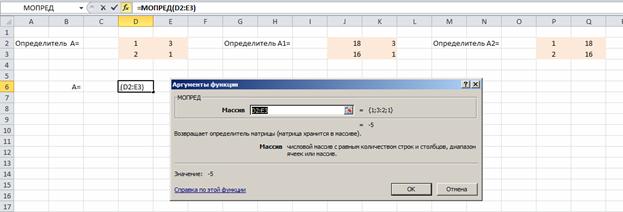
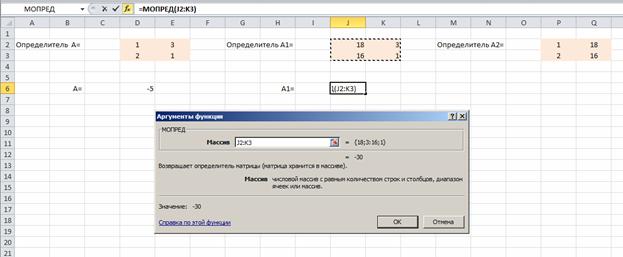
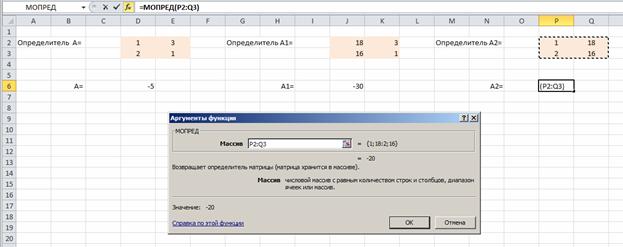
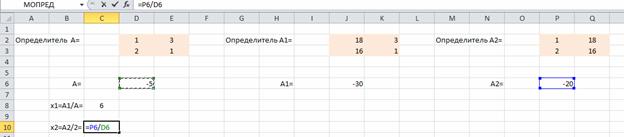
Находим значения х1 и х2
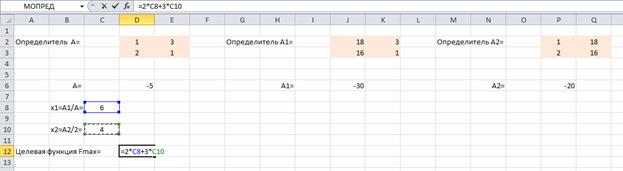
Подставляем координаты точки в целевую функцию
Fmax= 2×6 +3×4 = 24
Ответ: Fmax= 24 при x1=6 и x2=4.



