Оптимальное распределение оборудования
Оборудование m различных видов нужно распределить между n рабочими участками. Производительность единицы оборудования i-го вида на j-м рабочем участке равна равна pij;; i = 1,…,m; j = 1,…,n. Потребность j-го участка в оборудовании составляет bj , j = 1,…,n. Запас оборудования i-го вида равен ai , i = 1,…,m. Найти распределение оборудования по рабочим участкам, при котором суммарная производительность максимальна.Данная задача относится к классу транспортных задач при условии, что производительность линейно зависит от количества используемого оборудования. Поставщиками в задаче являются различные виды оборудования, потребителями – рабочие участки.
Обозначим через xij число единиц оборудования i-го вида, выделенное на j-й рабочий участок, i = 1,…,m; j = 1,…,n. Математическая модель задачи имеет следующий вид:
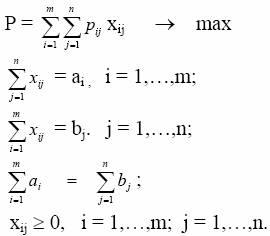
Построенная модель является сбалансированной. Если запас оборудования и потребность в нем не равны, то переход к сбалансированной модели осуществляется с помощью преобразований. В данной задаче требуется максимизировать целевую функцию Р, представляющую суммарную производительность. Для перехода к стандартной транспортной модели надо заменить функцию Р на противоположную функцию –Р, которую нужно будет минимизировать. При решении в матрице вместо стоимостей перевозок единицы груза будут стоять производительности, взятые с противоположным знаком. Далее задача решается методом потенциалов.
Перейти к решению транспортной задачи
Станковая задача
Решается задача, относящаяся к классу задач распределения оборудования (станковая задача). На промышленном предприятия в механическом цехе имеются несколько типов станков, каждый из которых может производить однотипные детали. Производительность каждого типа станка для данного типажа деталей различна. Различны также издержки производства, связанные с потреблением электроэнергии, амортизацией оборудования и т.д.Необходимо распределить заказ на изготовление определенного количества деталей в механическом цехе на смену так, чтобы издержки производства были минимальны.
| Тип станков | Количество станков в цехе | Средняя производительность на 1 станок в смену (дет.) | Средние издержки на производство сменной нормы на 1 станок (ден. ед) | Требуемая сменная производительность (количество деталей) |
| 1 | 15 | 50 | 400 | 1110 |
| 2 | 20 | 40 | 180 | |
| 3 | 40 | 25 | 150 |
x2- количество станков второго типа,
x3 - количество станков третьего типа,
Целевая функция
400x1+180x2+150x3 = min
Система ограничений
50x1+40x2+25x3 ≥ 1110
x1 ≤ 15, x2 ≤ 20, x3 ≤ 40.
Далее задачу можно решить графическим методом.



