Контрольная работа по математике
Задача 1. Дана система трех линейных уравнений. Найти решение ее двумя способами: методом Крамера и методом Гаусса.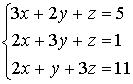
Скачать решение
Задача 2. Даны координаты вершин пирамиды А 1 А 2 А 3 А 4 . Найти:
- длину ребра А1А2;
- угол между ребрами А1А2 и А1А4;
- площадь грани А1А2А3;
- уравнение плоскости А1А2А3.
- объём пирамиды А1А2А3А4.
Скачать решение
Задача 3. Найти пределы функций:
3.1. а)
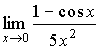 ; в)
; в) 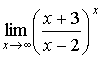 .
.
Задача 4. Найти значение производных данных функций в точке x=0:
Задача 5. Провести исследование функций с указанием
а) области определения и точек разрыва; б) экстремумов; с) асимптот.
По полученным данным построить графики функций.
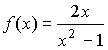 ;
;
Задача 6. Найти неопределенные интегралы:
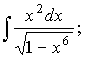 б)
б) Задача 7. Вычислить площади областей, заключённых между линиями:
y=3x-1; y=x2-2x+5.
Решение. С помощью сервиса
построение графика функции онлайнна координатной плоскости XY строим функции
y=3x-1; y=x2-2x+5.
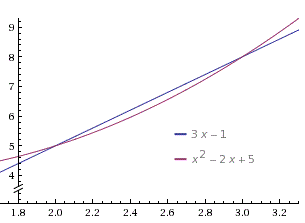
По рисунку видно, что площадь, заключенная между двумя линиями равна разнице площади между прямой y=3x-1 и площади параболы y=x2-2x+5. Для того, чтобы расставить пределы интегрирования, необходимо найти точки пересечения прямой и параболы. для этого используем сервис Решение уравнений онлайн. Получаем: x1=2; x2=3. Находим интеграл:
int(3*x-1-(x^2-2*x+5),x=2..3). Ответ: 1/6.
Примечание: пределы интегрирования можно найти другим способом. Находим,
3x-1-(x2-2x+5) = -x2+5x-6 и находим корни уравнения через формулу дискриминанта.