Динамические модели линейного программирования
Рассмотренные выше модели можно отнести к разряду статических моделей линейного программирования, поскольку в них временной интервал был фиксирован. Если возникает необходимость найти решение для другого временного интервала, то нужно заново вводить данные в модель и производить новую оптимизацию. Иначе говоря, в подходе, рассмотренном выше, предполагалось, что все временные интервалы являются независимыми и для каждого временного интервала должна решаться своя задача оптимизации.В динамических моделях рассматривается поведение системы на нескольких временных интервалах, а поиск решения производится один раз, оптимизируя поведение модели на всех временных интервалах сразу.
Динамические модели являются более реалистическими и более адекватно описывают многие производственные ситуации. Зависимость принятия решения от поведения системы во времени делает динамические модели исключительно полезным методом экономического анализа, но они оказываются значительно сложнее статических по своей постановке, содержат, как правило, большое число переменных, требуют определенного навыка при составлении табличной модели.
В качестве примера рассмотрим практически значимую модель управления производственными запасами (другое название этой модели – многофазовые модели управления запасами). Для общности результатов мы не будем присваивать параметрам числовые значения. После построения модели можно будет задать явные значения параметров и получить численное решение.
span class="examples">Пример
Рассмотрим химическую фирму, производящую полиуретан. Производитель имеет заказы на поставку полиуретана в количестве di тонн в месяц на ближайшие четыре месяца (i=1,2,…,4). Пусть затраты на производство одной тонны полиуретана составляют Ci тыс. рублей, а максимальный объем производства полиуретана по месяцам ограничен и равен Ki тонн в месяц. Производственная фирма имеет возможность хранить продукцию на складе, причем стоимость хранения одной тонны продукции за месяц составляет ni тыс. рублей. На начальный период времени запас полиуретана на складе составлял L0 тонн. Менеджеру компании требуется составить план производства полиуретана по месяцам, который бы обеспечил выполнение заказов при минимальной стоимости производства и хранения продукта.
Решение
Заметим, что если бы не было возможности хранить продукцию на складе, то задача разбилась бы на четыре независимые статические задачи и потеряла бы для нас всякий смысл.
Составим уравнение материального баланса, позволяющего вычислить количество продукции, хранящееся на складе в течение i-го месяца. Пусть xi– количество полиуретана, произведенного в i-й временной период. Тогда в течение первого месяца товарный запас на складе будет равен L1=L0+x1-d1. Товарный запас второго месяца
:
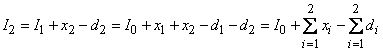
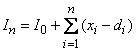. (3.24)
После того как мы вывели уравнение (3.24), описывающее поведение товарных запасов, легко записать математическую модель задачи:
(3.25)
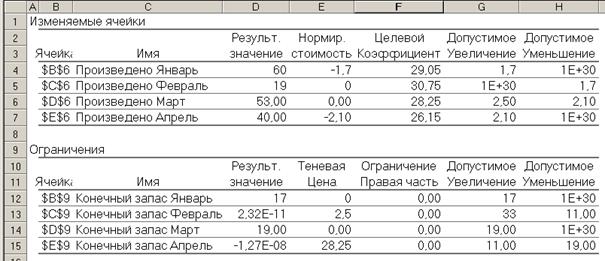
Поставленная задача (3.25) является типичной задачей линейного программирования и может быть достаточно легко решена с помощью программы Поиск решения. Используя численные значения удельных затрат производства
Удельные затраты производства и хранения полиуретана | Январь | Февраль | Март | Апрель |
Производство, тыс. руб | 28,00 | 30,00 | 27,80 | 26,00 |
Хранение, тыс. руб | 0,30 | 0,30 | 0,30 | 0,30 |
Объем поставок и производственные мощности, т | Январь | Февраль | Март | Апрель |
Ограничения по объему производства | 60 | 52 | 64 | 40 |
Объем поставок | 58 | 36 | 34 | 59 |
требуется составить оптимальный план производства полиуретана, если на первое января запас полиуретана на складе составлял 15 тонн.
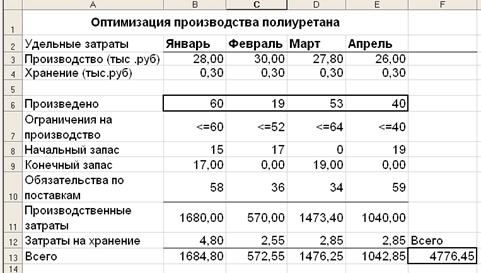
Табличная модель задачи управления запасами
Табличная модель задачи после нахождения оптимального решения приведена на рис. 21.
