Производственная задача линейного программирования
Фабрика выпускает продукцию двух видов: П1 и П2. Продукция обоих видов поступает в оптовую продажу. Для производства этой продукции используются три исходных продукта - А, В, С. Максимально возможные суточные запасы этих продуктов составляют 6, 8 и 5 т соответственно. Расходы сырья А, В, С на 1 тыс. изделий П1 и П2 приведены в табл.| Исходный продукт | Расход исходных продуктов на 1 тыс. изделий (т) | Максимально возможный запас (т) | |
| П1 | П2 | ||
| А В С | 1 2 1 | 2 1 0.8 | 6 8 5 |
Оптовые цены 1 тыс. шт. изделий П1 равны 3 тыс. руб., 1 тыс. шт. П2 - 2 тыс. шт.
Какое количество изделий (в тыс. шт.) каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?
В рассматриваемом примере имеем следующее:
Переменные.
Так как нужно определить объёмы производства каждого вида продукции, переменными являются:
X1 - суточный объём производства изделия П1в тыс. шт.;
Х2 - суточный объём производства изделия П2в тыс. шт.
Целевая функция. Так как стоимость 1 тыс. изделий П1 равна 3 тыс. руб., суточный доход от её продажи составит 3Х1тыс. руб. Аналогично доход от реализации Х2 тыс. шт. П2 составит 2Х2 тыс. руб. в сутки. При допущении независимости объёмов сбыта каждого из изделий общий доход равен сумме двух слагаемых - дохода от продажи изделий П1 и дохода от продажи изделий П2.
Обозначив доход (в тыс. руб.) через f(X), можно дать следующую математическую формулировку целевой функции: определить (допустимые) значения X1 и Х2, максимизирующие величину общего дохода:
f(X) = 3X1 + 2X2, Х = (Х1, Х2)
Ограничения. При решении рассматриваемой задачи должны быть учтены ограничения на расход исходных продуктов А, В и С и спрос на изготовляемую продукцию, что можно записать так:
≤
Максимально возможный запас данного исходного продукта
Это приводит к трём ограничениям:
Х1 + 2Х2 ≤ 6 (для А),
2Х1 + Х2 ≤ 8 (для В),
Х1 + 0.8Х2 ≤ 5 (для С).
Ограничения на величину спроса на продукцию имеют вид:
Х2 – X 1 ≤ 1 (соотношение величин спроса на изделия П1 и П2),
Х2 ≤ 2 (максимальная величина спроса на изделия П2).
Вводятся также условия неотрицательности переменных, т.е. ограничения на их знак:
X 1 ≥ 0 (объём производства П1)
Х2 ≥ 0 (объём производства П2).
Эти ограничения заключаются в том, что объёмы производства продукции не могут принимать отрицательных значений.
Следовательно, математическая модель записывается следующим образом.
Определить суточные объёмы производства (X 1 и Х2) изделий П1 и П2 в тыс. шт., при которых достигается
max f(X) = 3 X 1 + 2 X 2 (целевая функция)
при ограничениях:
X1 + 2Х2 ≤ 6
2Х1 + Х2 ≤ 8
X1 + 0.8Х2≤
5 - X1 + Х2 ≤ 1
Х2 ≤ 2
X1 ≥0, Х2≥ 0
Ресурсная задача
Для изготовления изделий типа А и В используется сырье трех видов, запасы каждого из которых Р1, Р2, Р3. На производство одного изделия типа А требуется затратить а1 кг сырья первого вида, а2 кг сырья второго вида, а3 кг сырья третьего вида. На одно изделие типа В расходуется соответственно b1, b2, b3 кг сырья каждого вида. Прибыль от реализации единицы изделия А составляет α ден.ед., а изделия В – β ден.ед. Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации. Решить задачу симплекс-методом. Дать геометрическое истолкование задачи.Математическая модель задачи
2x1 + x2≤438
3x1 + 6x2≤747
4x1 + 7x2≤812
F(X) = 7x1 + 5x2 => max
Задача об использовании ресурсов (задача планирования производства)
Для изготовления двух видов продукции Р1 и Р2 используют три вида ресурсов S1, S2, S3.Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в табл. 1.Таблица 1
Вид ресурса | Число единиц продукции, затрачиваемых на изготовление единицы продукции | Запасы ресурсов | |
| Р1 | Р2 | ||
| S1 | 2 | 3 | 20 |
| S2 | 3 | – | 18 |
| S3 | 1 | 4 | 10 |
Прибыль, получаемая от единицы продукции Р1 и Р2 – соответственно 2 и 3 д.е. Необходимо составить такой план производства продукции, при котором прибыль от её реализации будет максимальной.
Решение. Составим экономико-математическую модель задачи. Обозначим через х1, х2 – количество единиц продукции Р1 и Р2 соответственно. Тогда суммарная прибыль F составит 2x1 д.е. от реализации продукции Р1 и 3х2д.е. от реализации продукции Р2, то есть
F = 2x1 + 3x2. (1)
Поскольку количество ресурсов, необходимых для производства продукции ограниченно, составим систему ограничений по ресурсам. Для изготовления продукции потребуется (2x1 + 3x2) единиц ресурса S1, 3x1 единиц ресурса S2 и (x1 + 4x2) единиц ресурса S3. Так как потребление ресурсов S1, S2, S3 не должно превышать их запасов, 20, 18, 10 единиц, соответственно, то связь между потреблением ресурсов и их запасами выразится системой ограничений неравенств:
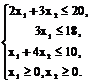(2)
Итак, экономико-математическая модель задачи: найти такой план выпуска продукции 
, удовлетворяющий системе ограничений (2), при котором целевая функция (1) принимает максимальное значение.
Задачу об использовании ресурсов можно обобщить на случай выпуска n видов продукции с использованием m видов ресурсов.
Обозначим через x (j = 1, 2,…,n) – число единиц продукции Pj, запланированной к производству; b1 (i = 1, 2,…,m) – запасы ресурсов Si, aij – число единиц ресурса Si, затрачиваемого на изготовление единицы продукции Pj; cj – прибыль от реализации единицы продукции Pj. Тогда экономико-математическая модель задачи в общей постановке примет вид:
F=c1x1+c2x2+…+cnxn→(max) (3)
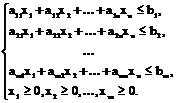(4)
Найти такой план 
выпуска продукции, удовлетворяющий системе (4), при котором функция (3) принимает максимальное значение.
Замечание. Данную задачу называют ещё задачей определения оптимального ассортимента продукции.
Производственная задача на минимум
Бригада приняла заказ на изготовление 57 шт. продукции П1, 68 шт. продукции П2 и 80 шт. продукции П3. Продукция производится на станках А и В. Для изготовления на станке А единицы продукции П1 требуется 15 мин, единицы продукции П2 – 50 мин, единицы продукции П3 – 27 мин, на станке В – соответственно 11, 15 и 13 мин.Постройте математическую модель задачи, на основании которой можно найти, сколько продукции и какого вида следует изготовить на станках А и В, чтобы заказ был выполнен в минимальное время.
Решение. Математическая модель задачи.
x1 - изготовлено продукции П1 на станке A, шт.
x2 - изготовлено продукции П1 на станке B, шт.
x3 - изготовлено продукции П2 на станке A, шт.
x4 - изготовлено продукции П2 на станке B, шт.
x5 - изготовлено продукции П3 на станке A, шт.
x6 - изготовлено продукции П3 на станке B, шт.
Ограничения по количеству:
x1 + x2≥ 57
x3 + x4 ≥ 68
x5 + x6 ≥ 80
Целевая функция:
15x1 + 11x2 + 50x3 + 15x4 + 27x5 + 13x6 = min
Задача оптимального производства продукции
Пример №1. Предприятие планирует выпуск двух видов продукции I и II , на производство которых расходуется три вида сырья А, В, и С. Потребность aij на каждую единицу j-го вида продукции i-го вида сырья, запас bi соответствующего вида сырья и прибыль cj от реализации единицы j-го вида продукции заданы таблицей:| Виды сырья | Виды продукции | Запасы сырья | |
| I | II | ||
| А | a11 = n | a12 = 2 | b1 = mn+5n |
| В | a21 = 1 | a22 = 1 | b2 = m+n+3 |
| С | a31 = 2 | a32 = m+1 | b3 = mn+4m +n+4 |
| прибыль | c1 = m+3 | c2 = n+1 | |
| план (ед.) | x1 | x2 | |
- Для производства двух видов продукции I и II с планом x1 и x2 единиц составить целевую функцию прибыли Z и соответствующую систему ограничений по запасам сырья, предполагая, что требуется изготовить в сумме не менее n единиц обоих видов продукции.
- В условиях задачи 1 составить оптимальный план ( x1, x2) производства продукции, обеспечивающий максимальную прибыль Zmax. Определить остатки каждого вида сырья. (Задачу решить симплекс–методом)
- Построить по полученной системе ограничений многоугольник допустимых решений и найти оптимальный план производства геометрическим путем. Определить соответствующую прибыль Zmax.
Перейти к онлайн решению своей задачи
Пример №2. Фермер может выращивать 4 культуры на площади 80 га. Он уже вложил соглашения на продажу определенной продукции (объем продаж) и может приобрести 250ц минеральных удобрений.
Площадь пропашных культур (подсолнечник, сахарная свекла, картофель, кукуруза) должна быть 20 га.
Затраты труда и удобрений, прибыль с 1 га приведены в таблице 2.
Определить, какие площади следует отвести под каждую культуру, чтобы получить максимальную прибыль.
Разработать экономико-математическую модель и решить задачу.
Выходные данные взять согласно варианту (таблица 2)
Решение.
x1 – площадь под гречку, га; x2 – площадь под ячмень, га; x3 – площадь под просо, га; x4 - площадь под картофель, га
Целевая функция: 140x1 + 110x2 + 120x3 + 380x4 → max
Ограничения по затратам на удобрение
3x1 + 3x2 + 2x3 + 5x4 ≤ 250
Ограничения по объемам продаж
10x1 + 30x2 + 25x3 + 180x4 ≤ 200
Ограничения по площади
x1 + x2 + x3 + x4 ≤ 80
Ограничения по площади пропашных культур
x4 ≤ 20
Итого имеем следующую ЗЛП
3x1 + 3x2 + 2x3 + 5x4 ≤ 250
10x1 + 30x2 + 25x3 + 180x4 ≤ 200
x1 + x2 + x3 + x4 ≤ 80
x4 ≤ 20
x1, x2, x3, x4 ≤ 0
Целевая функция: 140x1 + 110x2 + 120x3 + 380x4 → max
