Задача о раскрое или минимизации отходов (обрезков)
см. Модели линейного программирования для решения задач раскроя.Пример №1. Продукция бумажной фирмы выпускается в виде бумажных рулонов стандартной ширины - по 2 метра. По специальным заказам потребителей фирма поставляет рулоны и других размеров, для чего производится разрезание стандартных рулонов. Типичные заказы на рулоны нестандартных размеров приведены в табл.
| Заказ | Ширина рулона (м) | Количество рулонов |
| 1 | 0,5 | 150 |
| 2 | 0,7 | 200 |
| 3 | 0,9 | 300 |
Требуется найти такие сочетания различных вариантов разрезания стандартных рулонов, чтобы поступившие заказы полностью удовлетворить с минимальными потерями (отходами).
Рассмотрим все возможные варианты раскроя стандартного рулона, соответствующие данные приведем в табл.
| Ширина рулона(м) | Варианты раскроя рулона | Минимальное количество рулонов | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 0,5 | 0 | 2 | 2 | 4 | 1 | 0 | 150 |
| 0,7 | 1 | 1 | 0 | 0 | 2 | 0 | 200 |
| 0,9 | 1 | 0 | 1 | 0 | 0 | 2 | 300 |
| Отходы в м | 0,4 | 0,3 | 0,1 | 0 | 0,1 | 0,2 | - |
Определим переменные:
Xj - количество стандартных рулонов, разрезаемых по варианту j, j =1, 2, 3,4,5, 6.
Ограничения непосредственно связаны с требованием обеспечить изготовление требуемого количества нестандартных рулонов. Используя данные табл., получим:
2Х2 + 2 Х3 + 4 Х4 + Х5= 150 - количество рулонов шириной 0,5 м,
X1 + Х2 + 2 Х5 = 200 - количество рулонов шириной 0,7 м,
X1 + Х3 + 2 Х6 =300 - количество рулонов шириной 0,9 м.
Выражение для суммарной величины потерь бумаги (отходы) (в м) имеет вид
0,4Х1 + 0,3 Х2 + 0,1 Х3 + 0,1 Х5 + 0,2 Х6.
Таким образом, математическая модель в общем виде имеет вид
min f(x) = 0,4 X1 + 0,3Х2 + 0,1Х3 + 0,1Х5 + 0,2Х6.
при ограничениях:
2Х2 + 2 Х3 + 4 Х4 + Х5 = 150
Х 2 + Х2 + 2 Х5 = 200
Х 2 + Х3 + 2 Х6 = 300
Задача о раскрое материалов
Данная задача состоит в разработке такого плана, который обеспечивает необходимый комплект изделий при минимальных отходах (по длине, площади, массе, стоимости и др.) при раскрое материалов или обеспечивает максимальное число комплектов изделий. Пример №2. Требуется разработать оптимальный план раскроя стандартных листов стали, обеспечивая выход планового числа заготовок разного вида при минимальных суммарных отходах, если известно, что из партии листовой стали необходимо нарезать четыре вида различных заготовок в количестве bi (i = 1, 2,…,4) штук. Лист стали стандартных размеров может быть раскроен четырьмя способами. Каждому возможному способу раскроя соответствует карта раскроя. Из карт раскроя известен выход заготовок в штуках разных видов aij (i = 1, 2,…4; j = 1,2,…,4), а также площадь отходов cj (j = 1, 2,…,n) при раскрое одного листа стали по j-му способу раскроя. Какое количество листов стали необходимо раскроить тем или иным способом, чтобы отходы были минимальными?Таблица 3
Виды | План-задание по количеству заготовок (b1) | Выход заготовок (шт) разных видов | |||
| 1 | 2 | 3 | 4 | ||
| 1 | 240 | 1 | 4 | 0 | 1 |
| 2 | 200 | 1 | 0 | 4 | 0 |
| 3 | 120 | 1 | 0 | 0 | 3 |
| 4 | 140 | 1 | 1 | 0 | 3 |
| Площадь отходов, м2 (cj) | 1,4 | 0,1 | 2,1 | 0,1 | |
Составим экономико-математическую модель задачи. Обозначим через xj – количество исходного материала (листов стали), которые необходимо раскроить по одному из способов j. Ограничения в задаче должны соответствовать плановому выходу заготовок различных видов. Целевая функция сводиться к нахождению минимума отходов при раскрое
F=1,4·x1+0,1·x2+2,1·x3+0,1·x4→(min)..
Ограничения по выходу заготовок i-го вида по всем j способам раскроя:
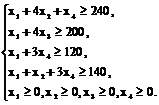
Пример №3. На раскрой (распил, обработку) поступает материал одного образца в количестве a единиц. Требуется изготовить из него l разных комплектующих изделий в количествах, пропорциональных числам b1, b2,…,bl (условие комплектности). Каждая единица материала может быть раскроена n различными способами, причем использование i-го способа (i = 1, 2,…,n) дает aik единиц k-го изделия (k = 1, 2,…,l). Необходимо найти план раскроя, обеспечивающий максимальное число комплектов.
Составим экономико-математическую модель задачи.
Обозначим через xi – число единиц материала, раскраиваемых i-ым способом, и x – число изготавливаемых комплектов изделий. Тогда целевая функция сводиться к нахождению
F=x→(max),
при ограничениях: по общему количеству материала равного сумме его единиц, раскраиваемых различными способами; по требованию комплектности и не отрицательности переменных.
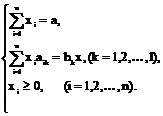
Пример №4. На предприятии имеются бревна длиной L м, которые необходимо разрезать на заготовки длиной l1, l2, l3 м в количестве p1, p2, p3 соответственно.
Необходимо составить оптимальный план раскройки материала, который обеспечивает минимальные отходы, при условии выполнения плана по выходу заготовок. Исходные данные приведены в таблице.
| Задача | Длина
бревен L, м | Размеры заготовок, м | Количество заготовок, шт. | ||||
| l1 | l2 | l3 | p1 | p2 | p3 | ||
| 68 | 6,5 | 2,1 | 2,3 | 1,4 | 600 | 720 | 900 |
Решение: Сначала составим математическую модель нашей задачи. Возможные варианты раскроя и отходы при каждом из них запишем в виде таблицы.
| Длина заготовки | Варианты раскроя | Количество заготовок | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| 2,1 | 3 | 2 | 2 | 1 | 1 | 0 | 0 | 600 |
| 2,3 | 0 | 1 | 0 | 1 | 0 | 2 | 1 | 720 |
| 1,4 | 0 | 0 | 1 | 1 | 3 | 1 | 3 | 900 |
| Остаток, м | 0,2 | 0 | 0,9 | 0,7 | 0,2 | 0,5 | 0 | |
Обозначим через xi количество бревен, разрезанных по i-му варианту (i=1..7). Тогда суммарный остаток отходов запишется в виде линейной функции:
Z = 0,2x1 + 0x2 + 0,9x3 + 0,7x4 + 0,2x5 + 0,5x6 + 0x7
При этом должны выполняться условия выполнения плана по количеству заготовок, т.е.
3x1 + 2x2 + 2x3 + x4 + x5 = 600
x2 + x4 + 2x6 + x7 = 720
x3 + x4 + 3x5 + x6 + 3x7 = 900
Таким образом, для решения поставленной задачи необходимо найти minZ при ограничениях. Поскольку minZ = -max(-Z(x)), то вместо задачи минимизации функции будем решать задачу максимизации функции:
Z = -(0,2x1 + 0x2 + 0,9x3 + 0,7x4 + 0,2x5 + 0,5x6 + 0x7)
Пример №5. Для пошива одного изделия требуется выкроить из ткани 6 деталей. На швейной фабрике были разработаны два варианта раскройки ткани. В таблице (расположенной ниже) приведены характеристики вариантов раскроя 10 м2 ткани комплектность, т.е. количество деталей определенного вида, которые необходимы для пошива одного изделия. Ежемесячный запас ткани для пошива изделий данного типа составляет 405 м2. В ближайший вечер планируется сшить 90 изделий.
Построить математическую модель задачи, позволяющий в ближайший месяц выполнить план по пошиву с минимальным количеством отходов.
Таблица - Характеристики вариантов раскроя отрезков ткани по 10м2
| Вариант раскроя | Количество деталей, шт./отрез | Отходы, м2/отрез | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 1 | 60 | 0 | 90 | 40 | 70 | 90 | 0,5 |
| 2 | 80 | 35 | 20 | 78 | 15 | 0 | 0,35 |
| Комплектность, шт./изделие | 1 | 2 | 2 | 2 | 2 | 2 | |
Математическая постановка задачи
Переменные задачи
В данной задаче искомые величины явно не указаны, но сказано, что должен быть выполнен ежемесячный план по пошиву 90 изделий. Для пошива 90 изделий в месяц требуется раскроить строго определенное количество деталей. Крой производится из отрезков ткани по 10 м2 двумя различными способами, которое позволяют получить различное число деталей. Поскольку заранее неизвестно, сколько ткани будет раскраиваться первым способом и сколько – вторым, то в качестве искомых величин можно задать количество отрезков ткани по 10м2, раскроенных каждым из способов:
x1 – количество отрезков ткани по 10м2, раскроенных первым способом в течении месяца, [отрез./мес.];
x2 – количество отрезков ткани по 10м2, раскроенных первым способом в течении месяца, [отрез./мес.];
Целевая функция
Целью решения задачи является выполнение плана при минимальном количестве отходов. Поскольку количество изделий строго запланировано (90 шт./мес.), то этот параметр не описывает ЦФ, а относится к ограничению, невыполнение которого означает, что задача не решена. А критерием эффективности выполнение плана служит параметр «количество отходов», который необходимо свести к минимуму. Поскольку при раскрое одного отреза (10м2) ткани по 1-му варианту получается 0,5м2 отходов, а по 2-му варианту – 0,35м2 (см. таблицу 1), то общее количество отходов при крое (ЦФ) имеет вид
L(x) = 0.5x1 + 0.35x2 = min,
Ограничения
Количество раскроев ткани различными способами ограничивается следующими условиями:
- Должен быть выполнен план по пошиву изделий, другими словами, общее количество выкроенных деталей должно быть таким, чтобы из него можно было пошить 90 изделий в месяц, а именно: 1-го вида должно быть как минимум 90 и деталей остальных видов – как минимум по 180 (см. комплектность в таблицу).
- Расход ткани не должен превышать месячного запаса на складе;
- Количество отрезков раскроенной ткани не может быть отрицательным.
Ограничение по плану пошива пальто имеют следующую содержательную форму записи.
(Общее количество деталей №1 выкроенных по всем вариантам)≥ (90 штук);
(Общее количество деталей №2 выкроенных по всем вариантам) ≥ (180 штук);
(Общее количество деталей №6 выкроенных по всем вариантам) ≥ (180 штук);
Математически эти ограничения записываются в виде:
60x1 + 80x2≥90;
35x2≥180;
90x1 + 20x2≥180;
40x1 + 78x2≥180;
70x1 + 15x2≥180;
90x1 ≥180;
Ограничение по расходу ткани имеет следующие формы записи:
Содержательную
(общее количество ткани, раскроенной за месяц)≤ (405м2)
Математическую
x1+x2≤405/10
Не отрицательность количества раскроенных отрезков задается в виде
x1 ≥ 0, x2 ≥ 0
Таким образом, математическая модель задачи имеет вид
L(x) = 0.5x1 + 0.35x2 = min [м2отх./мес.],
60x1 + 80x2≥90;
35x2≥180;
90x1 + 20x2≥180;
40x1 + 78x2≥180;
70x1 + 15x2≥180;
90x1 ≥180;
x1+x2≤40,5
x1 ≥ 0, x2 ≥ 0
Пример №6. Имеется 69 труб для отопительной сети по 1070 см каждая. Их необходимо разрезать на трубы по 130, 150 и 310 см. Найти такой вариант раскроя поступивших труб, при котором отходы были бы минимальными.
Решение.
Этап 1. Определяем варианты оптимального распила труб.
| Варианты раскроя | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 310 | 3 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 150 | 0 | 3 | 2 | 1 | 0 | 3 | 2 | 1 | 0 | 3 | 2 | 1 | 0 |
| 130 | 1 | 0 | 1 | 2 | 3 | 2 | 3 | 4 | 5 | 4 | 5 | 7 | 8 |
| Остатки | 10 | 0 | 20 | 40 | 60 | 50 | 70 | 90 | 110 | 100 | 120 | 10 | 30 |
Этап 2.
Составим экономико-математическую модель задачи. Обозначим через xj – количество труб, которые необходимо распилить по одному из способов j. Целевая функция сводиться к нахождению минимума отходов при распиле:
10x1 + 20x3 + 40x4 + 60x5 + 50x6 + 70x7 + 90x8 + 110x9 + 100x10 + 120x11 + 10x12 + 30x13 → min
x1 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10 + x11 + x12 + x13 = 69
Ответ: необходимо использовать только второй вариант распила (нулевые отходы)

