Линейное программирование
Введение в линейное программирование
Линейное программирование (ЛП) - наука о методах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения.Эта линейная функция называется целевой, а ограничения, которые математически записываются в виде уравнений или неравенств, называются системой ограничений.
В общем виде математическая модель задачи линейного программирования (ЗЛП) записывается как
при ограничениях:
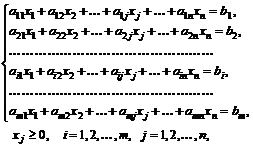
где xj - неизвестные; aij, bi, cj - заданные постоянные величины.
Все или некоторые уравнения системы ограничений могут быть записаны в виде неравенств.
Чтобы составить математическую модель задачи ЛП, необходимо:
- ввести обозначения переменных;
- учитывая ограничения в использовании экономических показателей задачи и их количественные закономерности, записать систему ограничений;
- исходя из цели экономических исследований, составить целевую функцию.
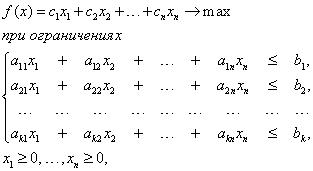
где ci, bj, aij постоянные коэффициенты. Это есть стандартная форма задачи ЛП. В общем случае ограничения могут иметь знак „
" или „=". Однако, умножая неравенство на -1 и заменяя равенство двумя неравенствами „≤" и „≥", можно придти к стандартной форме. Кроме того, взяв вместо f(x) функцию - f(x), можно получить задачу на минимум.
Обозначим через c=(c1 ,…,cn) - вектор коэффициентов целевой функции, b =(b1,…,bk) - вектор свободных членов ограничений,
- матрицу коэффициентов ограничений и запишем нашу задачу в векторной форме:
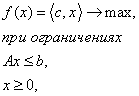
где
- скалярное произведение двух векторов c и x. Такая компактная запись удобна для теоретических исследований.
Несколько примеров задач, которые сводятся к задачам линейного программирования:
Задача оптимального раскроя материала. Фирма изготовляет изделие состоящее из р деталей. Причем в одно изделие эти детали входят в количествах k1 ,..., kr . С этой целью производится раскрой m партий материала. В i-ой партии имеется bi единиц материала. Каждую единицу материала можно раскроить на детали n способами. При раскрое единицы i-ой партии j-м способом получается аijr деталей r-го вида. Требуется составить такой план раскроя материала, чтобы из них получить максимальное число изделий.
Транспортная задача. Имеется n поставщиков и m потребителей одного и того же продукта. Известны выпуск продукции у каждого поставщика и потребности в ней каждого потребителя, затраты на перевозки продукции от поставщика к потребителю. Требуется построить план транспортных перевозок с минимальными транспортными расходами с учетом предложения поставщиков и спроса потребителей.
Задача о назначениях на работу. Имеется n работ и n исполнителей. Стоимость выполнения работы i исполнителем j равна cij. Нужно распределить исполнителей на работы так, чтобы минимизировать затраты на оплату труда.
3адача о смесях (о рационе). Из m видов исходных материалов каждый из которых состоит из n компонент, составить смесь, в которой содержание компонент должно быть не меньше b1 ,...,bn. Известны цены единиц материалов с1 ,...,сm и удельный вес j-го компонента в единице i-го материала. Требуется составить смесь, в которой затраты будут минимальными.
Задача о рюкзаке. Имеется n предметов. Вес предмета i равен рi , ценность – сi (i=1,...,n). Требуется при заданной ценности груза выбрать совокупность предметов минимального веса.
Основные свойства задачи линейного программирования
Приведем основные свойства задачи ЛП.1. Допустимое множество решений задачи ЛП либо пусто, либо является выпуклым многогранником в Rn (как пересечение полупространств, описываемых ограничениями-неравенствами). Оно может быть как ограниченным, так и неограниченным; в любом случае это замкнутый многогранник.
2. Если допустимое множество не пусто, а целевая функция ограничена сверху (для задачи максимизации, а для задачи минимизации - ограничена снизу) на этом множестве, то задача ЛП имеет оптимальное решение.
3. Оптимальные решения задачи ЛП (если они существуют) всегда находятся на границе допустимого множества. Точнее, если существует единственное оптимальное решение, то им является какая-либо вершина многогранника допустимых решений; если две или несколько вершин являются оптимальными решениями, то любая их выпуклая комбинация также является оптимальным решением (т.е. существует бесконечно много точек максимума или минимума).
Для любой задачи ЛП можно составить двойственную к ней задачу по следующим правилам.
1. Привести исходную задачу ЛП к стандартной форме.
2. Ввести новые переменные по числу основных ограничений исходной задачи.
3. Составить новые ограничения из новых переменных в виде линейных неравенств, знаки которых противоположны знакам неравенств исходной задачи, коэффициентами которых служат элементы транспонированной матрицы исходной задачи, а свободными членами - коэффициенты при целевой функции исходной задачи.
4. Для новых переменных написать условия неотрицательности.
В результате для исходной задачи (5.1) получим следующую двойственную задачу ЛП:
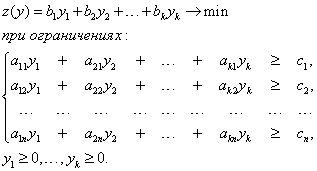
Задача (5.1) относительно задачи (5.3) называется прямой задачей ЛП . Векторная форма задачи (5.3) имеет вид:
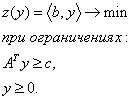
Рассмотрение взаимно двойственных задач ЛП полезно как с теоретической, так и с практической точек зрения. Это видно из следующих утверждений.
1. Если одна из задач (5.1) и (5.3) имеет оптимальное решение, то и другая имеет оптимальное решение, причем
2. Если целевая функция одной из задач неограниченна, то ограничения другой задачи несовместны (т.е. множество допустимых решений пусто).
3. Для того, чтобы допустимое решение
и 
были оптимальными решениями соответствующих задач (5.1) и (2.3) , необходимо и достаточно, чтобы
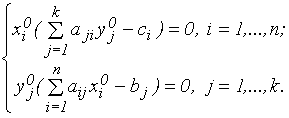
4. Для любых допустимых решений x0 и y0 справедливо неравенство f(x0 ) ≤ z(y0); если f(x0) = z(y0), то x0 и y0 - оптимальные решения задач (5.1) и (5.3).
5. Если прямая задача (5.1) моделирует максимизацию дохода при ограниченных ресурсах, то двойственная задача (5.3) при тех же предпосылках моделирует минимизацию затрат при фиксированном уровне дохода.
