Задача о рюкзаке
Назначение. Онлайн-калькулятор предназначен для решения задачи о ранце методами динамического программирования (прямой и обратной прогонки). см. пример решения.Задача о ранце
Имеются n предметов, которые необходимо поместить в рюкзак (ранец). Пусть известны вес aj и «ценность» cj каждого предмета (j= 1,2,... ,n). Требуется заполнить рюкзак, не превышая его грузоподъемности (объема) b и максимизируя суммарную ценность груза. Получаем следующую булеву ЗЦЛП (задача о рюкзаке):
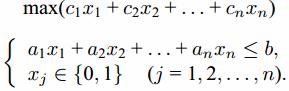
Задача о целочисленном рюкзаке
Предположим теперь, что каждый предмет имеется в неограниченном числе экземпляров, и требуется также максимизировать суммарную ценность груза, не превышая грузоподъемности. Получаем так называемую задачу о целочисленном рюкзаке:
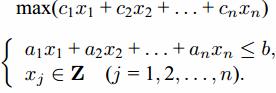
см. пример решения.
Пример решения задачи о рюкзаке.
Задание. В рюкзак объема V = 7 кладут N = 5 предметов.Объемы, веса и количество предметов в каждой группе приведены в таблице.
| Объем | 1 | 2 | 3 | 1 | 1 |
| Вес | 2 | 3 | 2 | 4 | 1 |
| Кол-во | 1 | 3 | 3 | 1 | 2 |
Максимизировать общий вес рюкзака.
Решение. I этап. Условная оптимизация.
f1(L) = max(2x1); 0 < x1 < 1; x1 = 0,1.
f1(0) = max[0*2] = 0
f1(1) = max[0*2, 1*2] = 2
f1(2) = max[0*2, 1*2] = 2
f1(3) = max[0*2, 1*2] = 2
f1(4) = max[0*2, 1*2] = 2
f1(5) = max[0*2, 1*2] = 2
f1(6) = max[0*2, 1*2] = 2
f1(7) = max[0*2, 1*2] = 2
Таблица 1 – Расчет значения функции f1(L)
| L | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| f1(L) | 0 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| x1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
f2(L) = max[3x2 + f1(L - 2x2)]; 0 < x2 < 3; x2 = 0,1,2,3.
f2(0) = max[0*3+0] = 0
f2(1) = max[0*3+2] = 2
f2(2) = max[0*3+2, 1*3+0] = 3
f2(3) = max[0*3+2, 1*3+2] = 5
f2(4) = max[0*3+2, 1*3+2, 2*3+0] = 6
f2(5) = max[0*3+2, 1*3+2, 2*3+2] = 8
f2(6) = max[0*3+2, 1*3+2, 2*3+2, 3*3+0] = 9
f2(7) = max[0*3+2, 1*3+2, 2*3+2, 3*3+2] = 11
Таблица 2 – Расчет значения функции f2(L)
| L | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| f2(L) | 0 | 2 | 3 | 5 | 6 | 8 | 9 | 11 |
| x2 | 0 | 0 | 1 | 1 | 2 | 2 | 3 | 3 |
f3(L) = max[2x3 + f2(L - 3x3)]; 0 < x3 < 3; x3 = 0,1,2,3.
f3(0) = max[0*2+0] = 0
f3(1) = max[0*2+2] = 2
f3(2) = max[0*2+3] = 3
f3(3) = max[0*2+5, 1*2+0] = 5
f3(4) = max[0*2+6, 1*2+2] = 6
f3(5) = max[0*2+8, 1*2+3] = 8
f3(6) = max[0*2+9, 1*2+5, 2*2+0] = 9
f3(7) = max[0*2+11, 1*2+6, 2*2+2] = 11
Таблица 3 – Расчет значения функции f3(L)
| L | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| f3(L) | 0 | 2 | 3 | 5 | 6 | 8 | 9 | 11 |
| x3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
f4(L) = max[4x4 + f3(L - 1x4)]; 0 < x4 < 1; x4 = 0,1.
f4(0) = max[0*4+0] = 0
f4(1) = max[0*4+2, 1*4+0] = 4
f4(2) = max[0*4+3, 1*4+2] = 6
f4(3) = max[0*4+5, 1*4+3] = 7
f4(4) = max[0*4+6, 1*4+5] = 9
f4(5) = max[0*4+8, 1*4+6] = 10
f4(6) = max[0*4+9, 1*4+8] = 12
f4(7) = max[0*4+11, 1*4+9] = 13
Таблица 4 – Расчет значения функции f4(L)
| L | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| f4(L) | 0 | 4 | 6 | 7 | 9 | 10 | 12 | 13 |
| x4 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
f5(L) = max[1x5 + f4(L - 1x5)]; 0 < x5 < 2; x5 = 0,1,2.
f5(0) = max[0*1+0] = 0
f5(1) = max[0*1+4, 1*1+0] = 4
f5(2) = max[0*1+6, 1*1+4, 2*1+0] = 6
f5(3) = max[0*1+7, 1*1+6, 2*1+4] = 7
f5(4) = max[0*1+9, 1*1+7, 2*1+6] = 9
f5(5) = max[0*1+10, 1*1+9, 2*1+7] = 10
f5(6) = max[0*1+12, 1*1+10, 2*1+9] = 12
f5(7) = max[0*1+13, 1*1+12, 2*1+10] = 13
Таблица 5 – Расчет значения функции f5(L)
| L | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| f5(L) | 0 | 4 | 6 | 7 | 9 | 10 | 12 | 13 |
| x5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
II этап. Безусловная оптимизация.
Таким образом, максимальный вес рюкзака f5(7) равна 13 кг.
При этом x5 = 0, так как f5(7) = 13 достигается при х5=0 (см. таблицу 5).
Предметы остальных типов распределяются следующим образом:
L = 7 - 1 * 0 = 7
f4(7) = 13 достигается при х4 = 1 (см. таблицу 4).
L = 7 - 1 * 1 = 6
f3(6) = 9 достигается при х3 = 0 (см. таблицу 3).
L = 6 - 3 * 0 = 6
f2(6) = 9 достигается при х2 = 3 (см. таблицу 2).
L = 6 - 2 * 3 = 0
f1(0) = 0 достигается при х1 = 0 (см. таблицу 1).
L = 0 - 1 * 0 = 0
В итоге наилучший вариант загрузки рюкзака достигается при значениях: x1 = 0, x2 = 3, x3 = 0, x4 = 1, x5 = 0



