Задача о целочисленном рюкзаке
Имеется транспортное средство грузоподъемностью L. Требуется заполнить его грузом, состоящим из предметов различных типов, чтобы стоимость всего груза оказалась максимальной.Для этого введем соответствующие обозначения:
Wi – вес одного предмета i-го типа;
Pi – стоимость одного предмета i-го типа;
xi – число предметов i-го типа, загружаемых на имеющееся транспортное средство.
Необходимо подобрать груз максимальной ценности с учетом грузоподъемности транспортного средства L.
Математически формализовать данную экстремальную задачу можно следующим образом:
при ограничениях:
xi =0,1,... (т.е. предметы груза неделимы).
Решение задачи разбивается на n этапов, на каждом их которых определяется максимальная стоимость груза, состоящего из предметов первого типа (первый этап), первого и второго типов (второй этап)
и т.д. Для этого воспользуемся рекуррентным соотношением или критерием оптимальности Беллмана:
fn (L) = max [ xnPn + fn-1(L-xnWn)], (2)
0<xn< [L/Wn],
где fn(L) – максимальная стоимость груза, состоящего из предметов n-го типа;
xnPn – стоимость взятых предметов n-го типа;
fn-1(L-xnWn) – максимальная стоимость груза, состоящего из предметов (n-1) типа с общим весом не более L-xnWn;
[L/Wn] – наибольшее целое число, не превосходящее L/Wn.
Будем считать f0(L) = 0 для любого L. Последовательно найдя значение функции f1(L), f2(L), ..., fn(L), можно получить полное решение сформулированной задачи.
Пример №1.
Пусть:
W1 = 4, W2 = 3, W3 = 2, W4 = 1 (единиц груза);
P1 = 28, P2= 20,P3 = 13, P4 = 6 (денежных единиц);
L = 10 (единиц груза).
Найдем последовательно значения функций: f1(L), f2(L), f3(L), f4(L) при различных значениях L (0<L<10).
f1(L) = max ( 28x1); 0<x1< [10/4]; x1 =0, 1, 2.
Таблица 1 – Расчет значения функции f1(L )
| L | 0-3 | 4-7 | 8-10 |
| f1(L) | 0 | 28 | 56 |
| x1 | 0 | 1 | 2 |
Таблица 2 – Расчет значения функции f2(L)
| L | 0-2 | 3 | 4-5 | 6 | 7 | 8 | 9 | 10 |
| f 2(L) | 0 | 20 | 28 | 40 | 48 | 56 | 60 | 68 |
| x2 | 0 | 1 | 0 | 2 | 1 | 0 | 3 | 2 |
Таблица 3 – Расчет значения функции f3(L)
| L | 0-1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| f 3(L) | 0 | 13 | 20 | 28 | 33 | 41 | 48 | 56 | 61 | 69 |
| x3 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
f4(L) = max [ x4 .6 + f3(L-x4. 1)]; 0<x4< [10/1]; x4 =0, 1, 2, …,10.
Таблица 4 – Расчет значения функции f4(L)
| L | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| f4(L) | 0 | 6 | 13 | 20 | 28 | 34 | 41 | 48 | 56 | 62 | 69 |
| x4 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
Таким образом, максимальная стоимость груза f4(10) равна 69 денежным единицам, при этом предметы четвертого типа загружать не следует, так как f4(10) = 69 достигается при х4=0 (см. таблицу 10).
Предметы остальных типов распределяются следующим образом:
х3= 1, так как f3(10) = 69 достигается при х3= 1 (см. таблицу 9), следовательно, вес этого предмета равен двум единицам груза, поэтому остальные предметы можно загрузить лишь в пределах веса, равного
10-2=8 единицам груза;
f2(8) = 56 достигается при х2 = 0 (см. таблицу 8), следовательно, предметы второго типа брать не следует;
f1(8) = 56 достигается при х1= 2 (см. таблицу 7), следовательно, предметов первого типа следует взять два.
В итоге наилучший вариант загрузки транспортного средства достигается при значениях х1= 2; х2= 0; х3= 1; х4= 0 (берутся два предмета первого типа и один – третьего типа).
Пример №2. Самолет загружается предметами N различных типов (табл. 1) с весом wj и стоимостью cj, j = 1,n. Максимальная грузоподъемность равна W=5. Определить максимальную стоимость груза, вес которого не более W.
Таблица 1 - Исходные данные
| Тип j | Вес wj | Стоимость cj |
| 1 | 2 | 65 |
| 2 | 3 | 80 |
| 3 | 1 | 30 |
Решение. Сделаем математическую постановку. Пусть xj – количество предметов j-го типа, загружаемых в самолет. Тогда математическая модель имеет вид:
xj ≥ 0 (3)
xj – целые. (4)
Отличительными особенностями задачи динамического программирования будут:
1. Этап j связан с загрузкой предметов j-го типа в количестве xj единиц (xj – управляемая переменная);
2. Состояние загружаемого самолета Sj на этапе j определяется через ограничение (2) математической модели (1) –(4). В алгоритме прямой прогонки состояния ![]() ; 0 ≤ Sj ≤ W; Sn = W
; 0 ≤ Sj ≤ W; Sn = W
В алгоритме обратной прогонки ![]()
3. Цель управления на этапе zj = cjxj.
4. Варианты решения xj этапа j описываются количеством предметов типа j: xj = 0,1,…, [W/wj]– целые.
Решим задачу методом обратной прогонки, загружая предметы с последнего типа (используя калькулятор).
Пусть Fj(Sj) – значение целевой функции (максимальная стоимость предметов, включенных на этапах j, j=1,..,n при заданном состоянии системы Sj
Рекуррентное соотношение для процедур обратной прогонки:
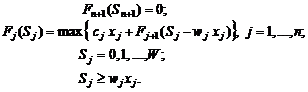
Этап 1.
F3(S3) = max{ c3x3};
x3 = 0,1,..,5;
S3 = 0,1,…,5;
S3 ≥ 1x3.
| S3 | c3x3 | opt | ||||||
| x3=0 | x3=1 | x3=2 | x3=3 | x3=4 | x3=5 | F3*(S3) | x3* | |
| 0 | 0 | – | – | – | – | – | 0 | 0 |
| 1 | 0 | 30 | – | – | – | – | 30 | 1 |
| 2 | 0 | 30 | 60 | – | – | – | 60 | 2 |
| 3 | 0 | 30 | 60 | 90 | – | – | 90 | 3 |
| 4 | 0 | 30 | 60 | 90 | 120 | – | 120 | 4 |
| 5 | 0 | 30 | 60 | 90 | 120 | 150 | 150 | 5 |
Этап 2. F2(S2) = max{c2x2 + F3(S2 – w2x2)}
x2 = 0,1
S2 = 0,1,..,5
S2 ≥ 2x2
S2 | c2x2 + F3(S2 – w2x2) | opt | ||||||||
| x2=0 | x2=1 | F2*(S2) | x2* | |||||||
| 0 | 0 + 0 = 0 | – | 0 | 0 | ||||||
| 1 | 0 +30 = 30 | – | 30 | 0 | ||||||
| 2 | 0 + 60 = 60 | – | 60 | 0 | ||||||
| 3 | 0 + 90 = 90 | 80 + 0 = 80 | 90 | 0 | ||||||
| 4 | 0 + 120 = 120 | 80 + 30 = 110 | 120 | 0 | ||||||
| 5 | 0 + 150 = 150 | 80 + 60 = 140 | 150 | 0 | ||||||
Значение условного оптимума F3(S3) берется из предыдущей таблицы.
Этап 3. F1(S1) = max{c1x1 + F2(S1 – w1x1)};
x1 = 0,1,2;
S1=5.
| S1 | c1x1 + F2(S1 – w1x1) | opt | |||
| x1=0 | x1=1 | x1=2 | F1*(S1) | x1* | |
| 5 | 0 + 150 = 150 | 65 + 90 = 155 | 130 + 30 +160 | 160 | 2 |
Определение управляемых переменных начинается с последней таблицы (обратный ход):
x1* = 2 → S1 = 2*2 = 4
S2 = 5-4 =1 → x2 = 0 → S3 = 1 – 0 = 1 → x3 = 1
Оптимальное решение X* = (2,0,1)
Пример №2. Имеется склад, на котором присутствует некоторый ассортимент товаров. Запас каждого товара неограничен. У каждого товара своя стоимость Ci и масса mi. Методом динамического программирования сформировать такой набор товаров, чтобы его суммарная масса не превышала заданную грузоподъемность М, и стоимость была бы максимальной.
Пример №3. На станок для обработки в течение цикла V = 4 мин. могут загружаться заготовки трех типов. В таблице1 содержатся исходные данные о суммарной продолжительности обработки заготовок i-го типа и их стоимости pi (i = 1, 2, 3). Ка-кими типами заготовок необходимо загрузить станок, чтобы суммарная стоимость обработанных деталей была максимальна?

