Задача оптимального распределения инвестиций
Назначение сервиса. Данный сервис предназначен для решения задачи оптимального распределения инвестиций в онлайн режиме. Результаты вычислений оформляются в отчете формата Word.Такого рода задачи основаны на функции Беллмана и при решении используется метод обратной прогонки (см. Типовые задания). Также можно воспользоваться сервисом Процедура прямой прогонки.
Инструкция. Выберите количество предприятий и количество строк (количество вариантов эффективного вложения), нажмите Далее (см. Пример заполнения). Если доход и остатки предприятий задан в виде функций f(x) и g(x), задача решается через этот калькулятор.
Пример №1. Определите оптимальный план расширения производства трех предприятий, если известна их прибыль в год при отсутствии вложений и при инвестировании 1, 2, 3 или 4 млн. Определите, при каком инвестировании будет максимальный процент прироста прибыли.
| f1 | f2 | f3 | xi |
| 40 | 30 | 35 | 0 |
| 90 | 110 | 95 | 1 |
| 395 | 385 | 270 | 2 |
| 440 | 470 | 630 | 3 |
| 620 | 740 | 700 | 4 |
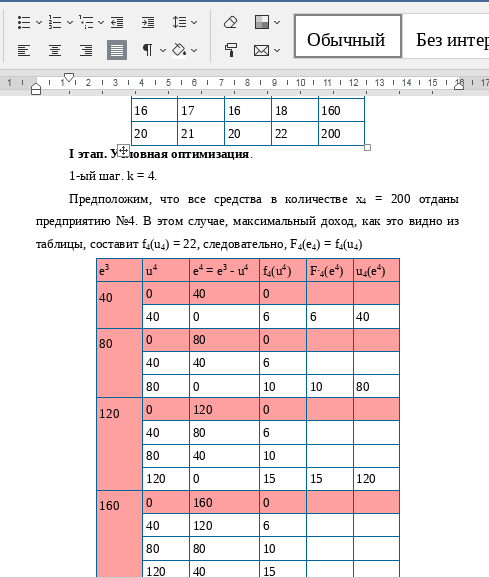
I этап. Условная оптимизация.
1-ый шаг. k = 3.
| e2 | u3 | e3 = e2 - u3 | f3(u3) | F*3(e3) | u3(e3) |
| 1 | 0 | 1 | 35 | ||
| 1 | 0 | 95 | 95 | 1 | |
| 2 | 0 | 2 | 35 | ||
| 1 | 1 | 95 | |||
| 2 | 0 | 270 | 270 | 2 | |
| 3 | 0 | 3 | 35 | ||
| 1 | 2 | 95 | |||
| 2 | 1 | 270 | |||
| 3 | 0 | 630 | 630 | 3 | |
| 4 | 0 | 4 | 35 | ||
| 1 | 3 | 95 | |||
| 2 | 2 | 270 | |||
| 3 | 1 | 630 | |||
| 4 | 0 | 700 | 700 | 4 |
2-ый шаг. k = 2.
| e1 | u2 | e2 = e1 - u2 | f2(u2) | F*2(e1) | F1(u2,e1) | F*2(e2) | u2(e2) |
| 1 | 0 | 1 | 30 | 95 | 125 | 125 | 0 |
| 1 | 0 | 110 | 0 | 110 | |||
| 2 | 0 | 2 | 30 | 270 | 300 | ||
| 1 | 1 | 110 | 95 | 205 | |||
| 2 | 0 | 385 | 0 | 385 | 385 | 2 | |
| 3 | 0 | 3 | 30 | 630 | 660 | 660 | 0 |
| 1 | 2 | 110 | 270 | 380 | |||
| 2 | 1 | 385 | 95 | 480 | |||
| 3 | 0 | 470 | 0 | 470 | |||
| 4 | 0 | 4 | 30 | 700 | 730 | ||
| 1 | 3 | 110 | 630 | 740 | 740 | 1 | |
| 2 | 2 | 385 | 270 | 655 | |||
| 3 | 1 | 470 | 95 | 565 | |||
| 4 | 0 | 740 | 0 | 740 |
3-ый шаг. k = 1.
| e0 | u1 | e1 = e0 - u1 | f1(u1) | F*1(e0) | F0(u1,e0) | F*1(e1) | u1(e1) |
| 1 | 0 | 1 | 40 | 125 | 165 | 165 | 0 |
| 1 | 0 | 90 | 0 | 90 | |||
| 2 | 0 | 2 | 40 | 385 | 425 | 425 | 0 |
| 1 | 1 | 90 | 125 | 215 | |||
| 2 | 0 | 395 | 0 | 395 | |||
| 3 | 0 | 3 | 40 | 660 | 700 | 700 | 0 |
| 1 | 2 | 90 | 385 | 475 | |||
| 2 | 1 | 395 | 125 | 520 | |||
| 3 | 0 | 440 | 0 | 440 | |||
| 4 | 0 | 4 | 40 | 740 | 780 | 780 | 0 |
| 1 | 3 | 90 | 660 | 750 | |||
| 2 | 2 | 395 | 385 | 780 | |||
| 3 | 1 | 440 | 125 | 565 | |||
| 4 | 0 | 620 | 0 | 620 |
Примечание: Столбцы 1 (вложенные средства), 2 (проект) и 3 (остаток средств) для всех трех таблиц одинаковы, поэтому их можно было бы сделать общими. Столбец 4 заполняется на основе исходных данных о функциях дохода, значения в столбце 5 берутся из столбца 7 предыдущей таблицы, столбец 6 заполняется суммой значений столбцов 4 и 5 (в таблице 3-го шага столбцы 5 и 6 отсутствуют).
В столбце 7 записывается максимальное значение предыдущего столбца для фиксированного начального состояния, и в 8 столбце записывается управление из 2 столбца, на котором достигается максимум в 7.
Этап II. Безусловная оптимизация.
Из таблицы 3-го шага имеем F*1(e0 = 4 млн.руб.) = 780 тыс.руб., то есть максимальная прибыль от инвестирования e0 = 4 млн.руб. равна 780 тыс.руб.
Из этой же таблицы получаем, что первому предприятию следует выделить u*1(e0 = 4 млн.руб.) = 0 млн.руб.
При этом остаток средств составит: e1 = e0 - u1, e1 = 4 - 0 = 4 млн.руб.
Из таблицы 2-го шага имеем F*2(e1 = 4 млн.руб.) = 740 тыс.руб., т.е. максимальная прибыль при e1 = 4 млн.руб. равна 740 тыс.руб.
Из этой же таблицы получаем, что второму предприятию следует выделить u*2(e1 = 4 млн.руб.) = 1 млн.руб.
При этом остаток средств составит: e2 = e1 - u2, e2 = 4 - 1 = 3 млн.руб.
Последнему предприятию достается 3 млн.руб. Итак, инвестиции в размере 4 млн.руб. необходимо распределить следующим образом: первому предприятию ничего не выделять, второму предприятию выделить 1 млн.руб., третьему предприятию выделить 3 млн.руб., что обеспечит максимальную прибыль, равную 780 тыс.руб.
Пример №2. Имеются 4 предприятия, между которыми необходимо распределить 100 тыс. усл. ед. средств. Значения прироста выпуска продукции на предприятии в зависимости от выделенных средств Х представлены в таблице. Составить оптимальный план распределения средств, позволяющий максимизировать общий прирост выпуска продукции.