Уравнение Беллмана
Условиями, которым должна удовлетворять общая задача оптимизации, чтобы её можно было описать моделью ДП, являются следующие:1. Задача должна интерпретироваться как n-шаговый процесс.
2. Целевая функция должна быть аддитивной, т. е. представляться в виде суммы показателей эффективности на каждом шаге.
3. Структура задачи должна быть определена для любого n и не зависеть от этого числа (принцип вложенности).
4. На каждом шаге система определяется конечным числом s параметров состояния и управляется конечным числом r переменных управления, причем s и r не зависят от k.
5. Выбор управления на k-м шаге не влияет на предшествующие шаги, а состояние в конце этого шага есть функция этого управления и предшествующего состояния (принцип отсутствия последействия).
Выполнение этих условий иногда оказывается очевидным, а иногда достигается после соответствующих преобразований. Чтобы построить модель ДП, необходимо выяснить, как на основе принципа оптимальности строится оптимальное уравнение n-шагового процесса.
Пусть система на k-м шаге под действием управления uk переходит из состояния εk-1в состояние εk. Из принципа отсутствия последействия имеем, что εk зависит только от εk-1 и uk.
Эти условия записываются в виде уравнений состояний:
εk = Tk(εk-1, uk), k = 1,..,n (5.1)
Из принципа оптимальности следует, что последующие управления uk+1, …, un должны выбираться оптимальными относительно состояния εk. Это значит, что при этих управлениях оптимизируется целевая функция на шагах k + 1 ,..., n.
Задача оптимизации процесса, начиная с (k + 1)-го шага, похожа на исходную задачу при начальном состоянии системы εk, управлении uk+1 = (uk+1 , …, un) и показателе эффективности Fk+1 = Fk+1(εk, uk+1, …, un). Выбрав оптимальное управление uk+1 = (u(k+1)*, …, un*) нa шагах k + 1,..., n, получим величину критерия 
, которая зависит только от εk – начального состояния для шагов k + 1,..., n.
Величина F*k+1(εk) называется условным максимумом.
Возникает задача, как выбрать оптимальное управление на k-м шаге, если известны оптимальные управления u(k+1)*,..., un* на последующих шагах k + 1,..., n и максимальное значение показателя эффективности F*k+1(εk) на этих шагах k + 1,...., n.
Так как состояние εk зависит от управления uk (5.1), то и величина F*k+1(εk) зависит от uk. Поэтому uk* необходимо выбирать так, чтобы это управление в совокупности с оптимальными управлениями u(k+1)*,..., un* приводило бы к общему максимуму показателя эффективности на шагах k + 1, …, n плюс данный шаг k. Аналитически это записывается так:
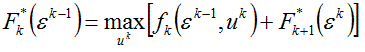. (5.2)
Это основное функциональное уравнение динамического программирования – уравнение Беллмана.
Оптимальное управление на k-м шаге uk*, при котором достигается максимум (5.2), зависит от состояния 
k* в начале k-го шага uk* = uk*(εk-1) – это условное оптимальное управление на k-м шаге.
Отметим особенность уравнения (5.2) для k = n:
,
т. к. F*n+1 = 0, поскольку (n + 1) шага нет.
Общими рекомендациями при построении модели ДП являются следующие:
1. Выбирается способ деления процесса на шаги.
2. Вводятся параметры состояния εk = (ε1k,…, εsk) и переменные управления uk = (u1k,..,urk)
3. Записываются уравнения состояний εk = Tk(εk-1, u k)
4. Из ограничений задачи определяется для каждого шага множество допустимых управлений Dk.
5. Вводятся показатели эффективности fk(εk-1, u k) и суммарный показатель 
.
6. Вводятся условные максимумы показателя эффективности от k-го шага до конца процесса F*k(εk-1) и условные оптимальные управления на k-м шаге uk*(εk-1).
7. Записываются функциональные уравнения Беллмана:
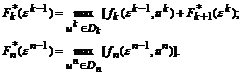
Рассмотрим построение модели ДП на примере.
Задача 1. Планируется распределение начальной суммы средств ε0 между n предприятиями П1, П2, …, Пn. Выделение предприятию Пk средств uk приносит доход fk(uk), 
. Определить, какое количество средств нужно выделить каждому предприятию, чтобы обеспечить максимальный суммарный доход.
Математическая модель задачи имеет вид
Построим модель динамического программирования.
Распределение средств между n предприятиями можно рассматривать как n-шаговый процесс. Поэтому за номер k-го шага процесса примем номер предприятия, которому выделяются средства uk. Очевидно, что переменные uk, k=1,n можно рассматривать как управляющие переменные. Начальное состояние системы характеризуется начальной величиной средств ε0. В конце первого шага состояние системы ε1= ε0-u1 характеризуется остатком средств после выделения предприятию П1 средств u1. Величины ε0, ε1,…, εn характеризуют остаток средств после распределения на предшествующих шагах, будем рассматривать их как параметры состояний. Уравнения состояний в этом случае имеют вид
εk= εk-1-uk, k=1,n
Найдем допустимые управления. Рассмотрим k-й шаг. Предприятию Пk можно выделить любое количество из имеющих к началу шага средств εk-1. Поэтому допустимое управление uk удовлетворяет неравенствам 0 ≤uk ≤ εk-1.
Показателем эффективности каждого шага является доход fk(uk), суммарным показателем – суммарный доход 
.
Тогда условным максимумом F*k(εk-1) будет максимальный суммарный доход на шагах k,…, n с начальным состоянием k-го шага εk-1. Условное оптимальное управление u*k(εk-1) будет определять оптимальное количество средств, выделяемых предприятию Пk, если остаток средств для распределения εk-1. Запишем теперь функциональные уравнения Беллмана:
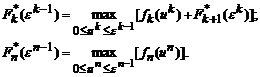(5.3)
Эти уравнения Беллмана соответствуют обратному ходу вычислений, т. е. когда мы движемся от n-го шага к первому.
