Замкнутые системы массового обслуживания

см. также Многоканальные модели систем массового обслуживания

Характеристики функционирования замкнутой одноканальной СМО

№ п/п	Предельные характеристики	Обозначения, формулы
1	Показатель (коэффициент) нагрузки системы, порождаемой каждым источником заявок	ρ = λ / μ
2	Показатель (коэффициент) нагрузки системы, порождаемой всеми i источниками заявок	iρ = iλ/μ
3	Вероятность того, что рабочий свободен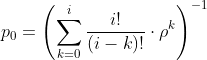
4	Вероятность состояний СМО	, k=1,..,i
5	Вероятность того, что рабочий занят	рзан = 1 – р0
6	Абсолютная пропускная способность СМО	A = pзан μ = (1 - p0)μ
7	Интенсивность выходящего потока обслуженных заявок	v=A=pзанμ = (1-p0)μ
8	Относительная пропускная способность	Q = 1
9	Среднее число заявок в системе (т.е. среднее число источников, находящихся в пассивном состоянии)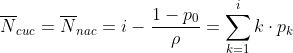
10	Средняя интенсивность среднего суммарного входящего потока заявок	Λ=(i-Nпас)·λ
11	Среднее число заявок, находящихся под обслуживанием	Nоб=1-p0
12	Среднее число заявок, находящихся в очереди
13	Коэффициент готовности – вероятность того, что произвольный источник находится в активном состоянии
14	Вероятность того, что в момент поступления заявки СМО находилась в состоянии sk	, k=0,..,i-1
15	Среднее время ожидания заявки в очереди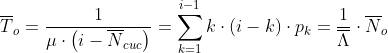
16	Среднее время обслуживания одной заявки
17	Среднее время пребывания заявки в системе	Tсис=Tо+Tоб или
18	Средняя производительность группы источников, находящихся в активном состоянии
19	Средняя потеря производительности за счёт группы источников, находящихся в пассивном состоянии

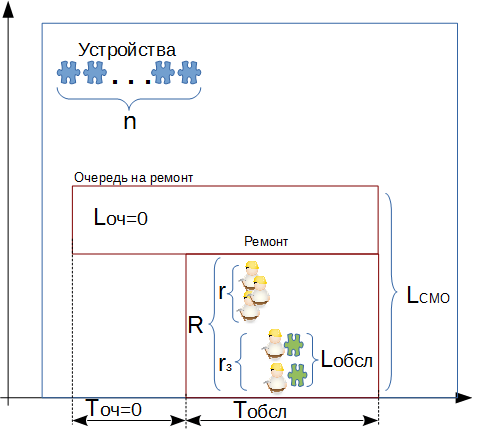
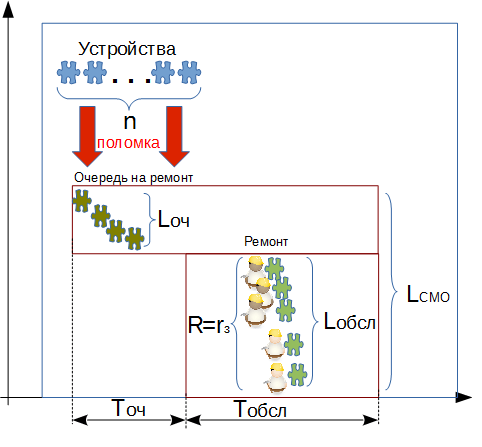
Пример №1. Один ремонтный рабочий обслуживает 6 подъемных устройств на станции технического обслуживания автомобилей. Интенсивность поломок каждого устройства равна 0.1 в сутки. Среднее время, которое тратит рабочий на обслуживание одного подъемника, равно t=7 часов. Найти предельные вероятности состояний данной СМО и найти среднее число неисправных подъемников, т.е. находящихся в ремонте и ожидающих ремонта. Определить также следующие характеристики:

1. вероятность того, что наладчик занят ремонтом подъемников;
2. абсолютную пропускную способность СМО;
3. относительную пропускную способность СМО;
4. среднее число подъемников в ремонте;
5. среднее число подъемников, ожидающих в очереди ремонта.

В калькулятор вводим следующие данные: количество обслуживающих устройств n=6, количество рабочих R=1, интенсивность потока заявок λ=0.1 (сутки);t_обс=7 (час.)

Решение. Переводим интенсивность потока заявок в часы: λ = 0.1/24 = 0.00417 час.
Интенсивность потока обслуживания:
μ = 1 / 7 = 0.143
Интенсивность нагрузки: ρ = λ*t_обс = 0.00417*7 = 0.0292
Определим вероятности состояния системы:
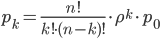, 1 ≤ k < R
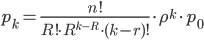, R ≤ k ≤ n






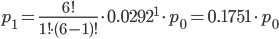
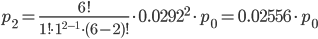
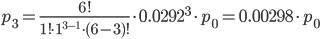
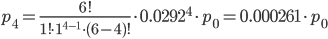
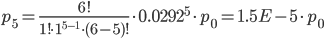
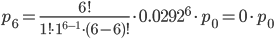
Учитывая, что ∑p_k = 1, и используя результаты расчета p_k, вычислим p₀:
∑p_k = p₀ + 0.1751p₀ + 0.02556p₀ + 0.00298p₀ + 0.000261p₀ + 1.5E-5p₀ + 0p₀
Откуда p₀ = 0.8306
Тогда: p₁ = 0.145; p₂ = 0.0212; p₃ = 0.00248; p₄ = 0.000217; p₅ = 1.3·10^-5; p₆ = 0;
Вероятность того, что наладчик занят ремонтом: p_3ан = 1 - p₀ = 1 - 0.8306 = 0.169
Значит, 17% из числа поступивших заявок не принимаются к обслуживанию.
1. Вероятность, что наладчик свободен: p₀ = 0.8306.
2. Относительная пропускная способность: Q = p_обс = 1 (в любом случае все подъемники попадут в очередь на ремонт и будут обслужены).
3. Абсолютная пропускная способность: A = p_зан*λ = 0.169*0.00417 = 0.000706 заявок/час.
Среднее время простоя СМО.
t_пр = p_отк*t_обс = 0.169*7 = 1.186 час.
Вероятность образования очереди.
p_оч = p₁ = 0.145
Вероятность отсутствия очереди.
p = 1 - p_оч = 1 - 0.145 = 0.855
4. Среднее число подъемников, ожидающих в очереди ремонт.
L_оч = ∑(k-R)*p_k = (1-1)*0.145 + (2-1)*0.0212 + (3-1)*0.00248 + (4-1)*0.000217 + (5-1)*1.3E-5 + (6-1)*0 = 0.0269
5. Среднее число подъемников, находящихся в ремонте.
L_обс = 1 - p₀ = 1 - 0.8306 = 0.169
6. Среднее число подъемников в системе (на обслуживании и в очереди).

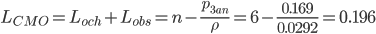
или
L_CMO = L_оч + L_обс = ∑k*p_k = 1*0.145 + 2*0.0212 + 3*0.00248 + 4*0.000217 + 5*1.3E-5 + 6*0 = 0.196
Коэффициент использования оборудования: I = (n - L_CMO)*λ = (6 - 0.196)0.00417 = 0.0242
7. Среднее число рабочих, простаивающих из-за отсутствия заявок.
r = p₀ = 0.8306
8. Среднее число рабочих, занятых обслуживанием.
r_з = R - r = 1-0.8306=0.169
9. Коэффициент занятости рабочих обслуживанием.

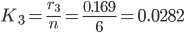
10. Коэффициент простоя оборудования в очереди.

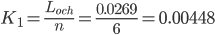
Коэффициент использования оборудования.

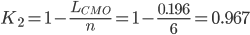
11. Коэффициент простоя рабочих.

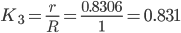
Следовательно, система на 17% занята обслуживанием, 83% времени находится в простое.
12. Среднее время ожидания заявки в очереди (время ожидания обслуживания в очереди). 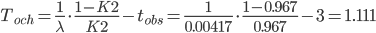час.
13. Среднее время пребывания заявки в СМО.

Пример №2. СМО состоит из n идентичных приборов, каждый из которых выходит из строя в случайные моменты времени с интенсивностью λ. В случае выхода прибора из строя он начинает сразу восстанавливаться одним из m свободных восстанавливающих устройств (ВУ) с интенсивностью μ. Если все ВУ заняты, то прибор встает в очередь и ждет до тех пор, пока не освободится ВУ. Каждое ВУ в любой момент времени может восстанавливать не более одного прибора. Требуется оценить надежность работы системы и дать предложения по повышению эффективности ее функционирования.