Многоканальная модель с пуассоновским входным потоком и экспоненциальным распределением длительности обслуживания
Модели с и обслуживающими каналами. В подавляющем большинстве случаев на практике системы массового обслуживания являются многоканальными, и, следовательно, модели c n обслуживающими каналами (где n >1) представляют не сомнений интерес.Процесс массового обслуживания, описываемый данной моделью, характеризуется интенсивностью входного потока l,при этом параллельно может обслуживаться не более пклиентов (заявок). Средняя продолжительность обслуживания одной заявки равняется 1/m. Входной и выходной потоки являются пуассоновскими. Режим функционирования того или иного обслуживающего канала не влияет на режим функционирования других обслуживающих каналов системы, причем длительность процедуры обслуживания каждым из каналов является случайной величиной, подчиненной экспоненциальному закону распределения. Конечная цель использования ппараллельно включенных обслуживающих каналов заключается в повышении (по сравнению с одноканальной системой) скорости обслуживания требований за счет обслуживания одновременно пклиентов.
Граф состояний многоканальной системы массового обслуживания с отказами имеет вид, показанный на рис. 3.3.с п обслуживающими каналами(где п >1) представляют несомненный интерес.

Рис. 3.3. Граф состояний многоканальной СМО с отказами
Состояния данной СМО имеют следующую интерпретацию:

P0(0) = 1.P1(0) = P2 (0) = … = Pk (0) = … = Pn (0) = 0
Cстационарное решение системы имеет вид:
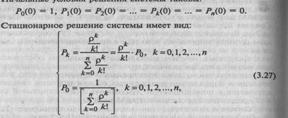
![]()
Формулы для вычисления вероятностей Рkназываются формулами Эрланга.
Определим вероятностные характеристики функционирования многоканальной СМО с отказами в стационарном режиме.
Вероятность отказа определяет формула
Вероятность того, что заявка будет принята к обслуживанию (она же - относительная пропускная способность системы q)дополняет Рткдо единицы:
Среднее число каналов, занятых обслуживанием (к), следующее: I
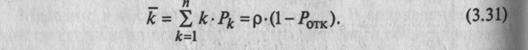
Величина кхарактеризует степень загрузки СМО.
Пример 3.4. Пусть n-канальная СМО представляет собой вычислительный центр (ВЦ) с тремя (n = 3) взаимозаменяемыми ПЭВМ для решения поступающих задач. Поток задач, поступающих на ВЦ, имеет интенсивность λ = 1 задаче в час. Средняя продолжительность обслуживания tобсл = 1,8 час. Поток заявок на решение задач и поток обслуживания этих заявок являются простейшими.
Требуется вычислить финальные значения:
- вероятности состояний ВЦ;
- вероятности отказа в обслуживании заявки;
- относительной пропускной способности ВЦ;
- абсолютной пропускной способности ВЦ;
- среднего числа занятых ПЭВМ на ВЦ.
Решение
1. Определим параметр μ потока обслуживании:
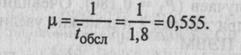
2. Приведенная интенсивность потока заявок равна:
ρ=λ/μ=1/0.555=1.8
3. Предельные вероятности состояний найдем по формулам Эрланга (3.27):
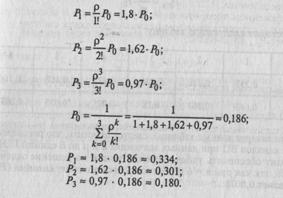
4. Вероятность отказа в обслуживании заявки
![]()
5. Относительная пропускная способность ВЦ
![]()
6. Абсолютная пропускная способность ВЦ
![]()
7. Среднее число занятых каналов - ПЭВМ
k=ρ·(1-PОТК)=1.8·(1-0.18)=1.476
Таким образом, при установившемся режиме работы СМО в среднем будет занято 1,5 компьютера из трех — остальные полтора будут простаивать. Работу рассмотренного ВЦ вряд ли можно считать удовлетворительной, так как центр не обслуживает заявки в среднем в 18% случаев (Р3 = 0,180). Очевидно, что пропускную способность ВЦ при данных μ и λможно увеличить только за счет увеличения числа ПЭВМ.
Определим, сколько нужно использовать ПЭВМ, чтобы сократить число не обслуженных заявок, поступающих на ВЦ, в 10 раз, т.е. чтобы вероятность отказа в решении задач не превосходила 0,0180. Для этого используем формулу (3.28):
![]()
Составим следующую таблицу:
| n | 1 | 2 | 3 | 4 | 5 | 6 |
| P0 | 0.357 | 0.226 | 0.186 | 0.172 | 0.167 | 0.166 |
| PОТК | 0.643 | 0.367 | 0.18 | 0.075 | 0.026 | 0.0078 |
Анализируя данные таблицы, следует отметить, что расширение числа каналов ВЦ при данных значениях λ и μ до 6 единиц ПЭВМ позволит обеспечить удовлетворение заявок на решение задач на 99,22%, так как при п= 6 вероятность отказа в обслуживании (Ротк) составляет 0,0078.

