Двумерная модель распределения ресурсов
Имеется начальное количество средств ε0, которое необходимо распределить в течение n лет между двумя предприятиями. Средства х, вложенные в предприятие 1, приносят к концу года доход f1(x) и возвращаются в размере ε 1(x) < x. Аналогично средства х, вложенные в предприятие 2, дают доход f2(x) и возвращаются в размере ε 2(x) < x. По истечении года все оставшиеся средства заново перераспределяются между предприятиями 1 и 2, новых средств не поступает, и доход в производство не вкладывается. Требуется найти оптимальный способ распределения имеющихся средств.Рассматриваемый процесс – n-шаговый, номер шага соответствует номеру года. Параметр состояния εk-1 ,k = 1…n – количество средств, которые следует перераспределить в начале k-го года. Переменные управления на каждом шаге xk1 и xk2 – количество средств, выделяемых соответственно предприятиям 1 и 2. Так как средства ежегодно перераспределяются полностью, то
xk2 = εk-1 – xk1, k = 1… n (1)
Поэтому для каждого шага задача становится одномерной: управление xk = xk1, тогда xk2 = εk-1 – xk1.
Показатель эффективности k-го шага Fk = f1(xk) + f2(ε k-1 - xk) – доход, полученный от двух предприятий в течение k-го года. Показатель эффективности всей задачи – доход, полученный от двух предприятий в течение n лет:
Уравнения состояния – остаток средств ε k после k-го шага:
εk = φ 1(xk) + φ 2(εk-1 - xk) (3)
На основе приведенных выше рассуждений можно записать рекуррентные соотношения Беллмана, которые будут иметь вид
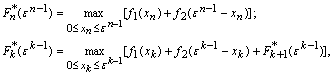
где ε k определяется из уравнения состояния.
Пример. Имеется начальное количество средств ε0 = 10 000, которое необходимо распределить в течение трех лет между двумя предприятиями. Средства х, вложенные в предприятие 1, приносят к концу года доход f1(x) = 0,4x и возвращаются в размере φ 1(x) = 0,5x. Аналогично средства х, вложенные в предприятие 2, дают доход f2(x) = 0,3x и возвращаются в размере φ 2(x) = 0,8x. По истечении года все оставшиеся средства заново перераспределяются между предприятиями 1 и 2, новых средств не поступает, и доход в производство не вкладывается. Требуется найти оптимальный способ распределения имеющихся средств.
Решение проводим с помощью калькулятора. Показатель эффективности k-го шага равен
Fk = 0,4xk + 0,3(εk-1 - xk) = 0,1xk + 0,3εk-1
уравнение состояния принимает вид
εk = 0,5xk + 0,8(ε k-1 - xk ) = 0,8ε k-1 – 0,3xk
Тогда рекуррентные соотношения Беллмана запишутся следующим образом:
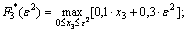
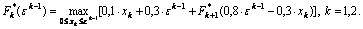
Fk = 0,4xk + 0,3(εk-1 - xk) = 0,1xk + 0,3εk-1
уравнение состояния принимает вид
εk = 0,5xk + 0,8(ε k-1 - xk ) = 0,8ε k-1 – 0,3xk
Тогда рекуррентные соотношения Беллмана запишутся следующим образом:
Проведем этап условной оптимизации.
3-й шаг:
так как показатель эффективности F3*(ε2) является линейной функцией относительно x3 и эта переменная входит в выражение со знаком плюс, то он достигает максимума в конце интервала 0 ≤x3 ≤ ε2, т.е. при x3 = ε2.
2-й шаг:
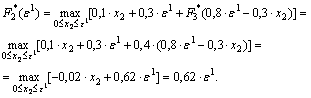
так как показатель эффективности F2*(ε1) является линейной функцией относительно x2 и эта переменная входит в выражение со знаком минус, то он достигает максимума в начале интервала 0 ≤x2 ≤ ε1, т. е. при x2 = 0.
1-й шаг:
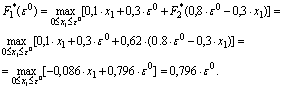
так как показатель эффективности F1*(ε0) является линейной функцией относительно x1 и эта переменная входит в выражение со знаком минус, то он достигает максимума в начале интервала 0 ≤x1 ≤ ε0, т. е. при x1 = 0.
Этап безусловной оптимизации.
Так как ε0 = 10 000, то Fmax = F1*(ε0) = 7960 и x1 = 0. Зная x1, находим ε1 = 0,8*10000 – 0,3*0 = 8000.
Так как ε1 = 8000 и x2 = 0, то ε2 = 0,8*8000 – 0,3*0 = 6400.
Далее находим x3, поскольку x3 = ε2, x3 = 6400.
В результате средства по годам (табл.) оптимальным образом распределяются так:
| Предприятие | 1-й год | 2-й год | 3-й год |
| 1 | 0 | 0 | 6 400 |
| 2 | 10 000 | 8 000 | 0 |

