Табличный метод расчета параметров сетевого графика
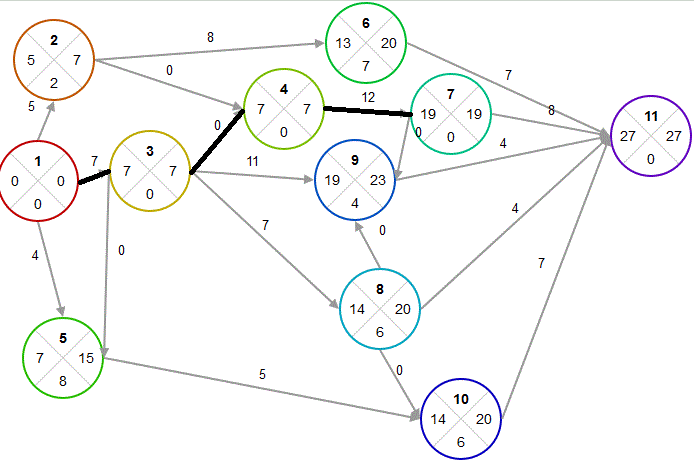
Помимо табличного метода существуют следующие способы расчета: графический метод, метод потенциалов.Пример. Определить временные параметры сетевого графика на рисунке, пользуясь табличным методом.
Решение проводим через калькулятор: все вычисления будем заносить в таблицу 3.
Перечень работ и их продолжительность перенесем во вторую и третью графы. При этом работы следует записывать в графу 2 последовательно: сначала начиная с номера 1, затем с номера 2 и т.д.
В первой графе поставим число, характеризующее количество непосредственно предшествующих работ (КПР) тому событию, с которого начинается рассматриваемая работа. Так, для работы (5,10) в графу 1 поставим число 2, т.к. на номер 5 оканчиваются 2 работы: (1,5) и (3,5).
Таблица 3 – Табличный метод расчета сетевого графика
| КПР | Код Работы | Продолжительность работы | Ранние сроки | Поздние сроки | Резервы времени | |||||||||||
| (i,j) | t(i,j) | tрн(i,j) | tро(i,j) | tпн(i,j) | tпо(i,j) | Rп | Rс | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||||
| 1 | 2 | 3 | 4 | 5=3+4 | 6=7-3 | 7 | 8 | 9 | ||||||||
| 0 | (1,2) | 5 | 0 | 5 | 2 | 7 | 2 | 0 | ||||||||
| 0 | (1,3) | 7 | 0 | 7 | 0 | 7 | 0 | 0 | ||||||||
| 0 | (1,5) | 4 | 0 | 4 | 11 | 15 | 11 | 3 | ||||||||
| 1 | (2,4) | 0 | 5 | 5 | 7 | 7 | 2 | 2 | ||||||||
| 1 | (2,6) | 8 | 5 | 13 | 12 | 20 | 7 | 0 | ||||||||
| 1 | (3,4) | 0 | 7 | 7 | 7 | 7 | 0 | 0 | ||||||||
| 1 | (3,5) | 0 | 7 | 7 | 15 | 15 | 8 | 0 | ||||||||
| 1 | (3,8) | 7 | 7 | 14 | 13 | 20 | 6 | 0 | ||||||||
| 1 | (3,9) | 11 | 7 | 18 | 12 | 23 | 5 | 1 | ||||||||
| 2 | (4,7) | 12 | 7 | 19 | 7 | 19 | 0 | 0 | ||||||||
| 2 | (5,10) | 5 | 7 | 12 | 15 | 20 | 8 | 2 | ||||||||
| 1 | (6,11) | 7 | 13 | 20 | 20 | 27 | 7 | 7 | ||||||||
| 1 | (7,9) | 0 | 19 | 19 | 23 | 23 | 4 | 0 | ||||||||
| 1 | (7,11) | 8 | 19 | 27 | 19 | 27 | 0 | 0 | ||||||||
| 1 | (8,9) | 0 | 14 | 14 | 23 | 23 | 9 | 5 | ||||||||
| 1 | (8,10) | 0 | 14 | 14 | 20 | 20 | 6 | 0 | ||||||||
| 1 | (8,11) | 4 | 14 | 18 | 23 | 27 | 9 | 9 | ||||||||
| 3 | (9,11) | 4 | 19 | 23 | 23 | 27 | 4 | 4 | ||||||||
| 2 | (10,11) | 7 | 14 | 21 | 20 | 27 | 6 | 6 | ||||||||
Графы 6 и 7 заполняются “обратным ходом”, т.е. “снизу вверх”. Для этого просматриваются строки, оканчивающиеся на номер последнего события, и из графы 5 выбирается максимальная величина, которая записывается в графу 7 по всем строчкам, оканчивающимся на номер последнего события (т.к. tр(i)= tп(i)). В нашем случае
t(11)=27. Затем для этих строчек находится содержание графы 6 как разности граф 7 и 3 по формуле (2.7). Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е.
10. Для определения графы 7 этих строк (работы (8,10) и (5,10)) просматриваются все строчки, начинающиеся с номера 10. В графу 6 среди них выбирается минимальная величина, которая переносится в графу 7 по обрабатываемым строчкам. В нашем случае она одна - (10,11), поэтому заносим в строчки (8,10) и (5,10) графы 7 цифру 20. Процесс повторяется до тех пор, пока не будут заполнены все строчки по графам 6 и 7.
Содержимое графы 8 равно разности граф 6 и 4 или граф 7 и 5 (формула (2.8).
Содержимое графы 9 вычисляется по формуле (2.9):
Rс(3,9)= tр.н(9,11)- tр.о.(3,9)=19-18=1.
Учитывая, что резерв времени имеют только события и работы, которые принадлежат критическому пути, получаем критический путь (1,3,4,7,11).
Перейти к онлайн решению своей задачи Пример №2
| Работа (i,j) | Количество предшествующих работ | Продолжительность tij | Сроки выполнения работ | Резервы времени | |||||
| ранние | поздние | работ | событий Rj | ||||||
| начало tijР.Н. | окончание tijР.О. | начало tijП.Н. | окончание tijП.О. | полный tijП | свободный tijС.В. | ||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| (0,1) | 0 | 15 | 0 | 15 | 0 | 15 | 0 | 0 | 0 |
| (1,2) | 1 | 16 | 15 | 31 | 15 | 31 | 0 | 0 | 0 |
| (1,3) | 1 | 6 | 15 | 21 | 22 | 28 | 7 | 0 | 7 |
| (2,4) | 1 | 6 | 31 | 37 | 31 | 37 | 0 | 0 | 0 |
| (3,5) | 1 | 5 | 21 | 26 | 28 | 33 | 7 | 0 | 7 |
| (4,6) | 1 | 8 | 37 | 45 | 37 | 45 | 0 | 0 | 0 |
| (5,6) | 1 | 6 | 26 | 32 | 39 | 45 | 13 | 13 | 0 |
| (5,7) | 1 | 8 | 26 | 34 | 35 | 43 | 9 | 0 | 9 |
| (5,8) | 1 | 14 | 26 | 40 | 33 | 47 | 7 | 7 | 0 |
| (6,8) | 2 | 2 | 45 | 47 | 45 | 47 | 0 | 0 | 0 |
| (7,8) | 1 | 4 | 34 | 38 | 43 | 47 | 9 | 9 | 0 |
| (8,9) | 3 | 3 | 47 | 50 | 47 | 50 | 0 | 0 | 0 |
а) графы 1 и 3 заполняются на основе исходных данных.
б) в графе 2 записывается количество предшествующих работ по сетевому графику или определяется из графы 1 по числу работ, имеющих второй цифрой в коде ту, с которой начинается данная работа.
г) в графе 4 раннее начало работ, выходящих из исходного события, а раннее окончание этих работ равно их продолжительности (гр. 5). Раннее начало последующих работ определяется путем выбора максимального из сроков раннего окончания предшествующих работ. Количество сравниваемых сроков равно количеству предшествующих работ графы 2. Раннее начало последующих работ можно определить после того, как найдено раннее окончание предшествующих. В свою очередь раннее окончание каждой работы находится как сумма величин раннего начала и продолжительности данной работы;
г) продолжительность критического пути определяется после заполнения граф 4 и 5 как максимальная величина из сроков раннего окончания работ, которые ведут к завершающему событию 9;
д) найденная величина критического пути ТKP дням заносится в графу 7 для всех работ, ведущих к завершающему событию. Затем заполнение ведется снизу вверх. Находятся все работы, следующие за рассматриваемой, и определяются разности между поздним окончанием этих работ и их продолжительностями. Минимальная из величин заносится в графу 7;
е) в графе 6 позднее начало работы определяется как разность позднего окончания этих работ и их продолжительности (из значений графы 7 вычитаются данные графы 3);
ж) в графе 8 полный резерв времени работы определяется разностью между значениями граф 7 и 5. Если он равен нулю, то работа является критической;
з) в графе 10 резерв времени событий j определяется как разность позднего окончания работы, заканчивающегося событием j графы 7, и ранним началом работы, начинающимся событием j;
и) значение свободного резерва времени работы определяется как разность значений графы 10 и данных графы 8 и указывает на расположение резервов, необходимых для оптимизации.
см. также автоматический расчет параметров сетевого графика

