Оптимизация сетевой модели по критерию затраты

Исходные данные:

События (предки)	начало работ	готовность деталей	готовность документации	поступление дополнительного оборудования	готовность блоков
События (потомки)	начало работ	готовность деталей	готовность документации	поступление дополнительного оборудования	готовность блоков
готовность деталей	изготовление деталей (4/3)
готовность документации		подготовка документации (5/2)		установка дополнительного оборудования (12/6)	составление инструкций (11/6)
поступление дополнительного оборудования	закупка дополнительного оборудования (10/5)
готовность блоков		сборка блоков (6/4)
готовность изделия			компоновка изделия (9/6)

Работы	Нормальный вариант		Ускоренный вариант			Прирост затрат на одни сутки ускорения
Работы	Время (сутки)	Затраты (у.е.)		Время (сутки)	Затраты (у.е.)	Прирост затрат на одни сутки ускорения
изготовление деталей	4	100		3	120	20
закупка дополнительного оборудования	10	150		5	225	15
сборка блоков	6	50		4	100	25
подготовка документации	5	70		2	100	10
установка дополнительного оборудования	12	250		6	430	30
составление инструкций	11	260		6	435	35
компоновка изделия	9	180		6	300	40
	ВСЕГО	1060		ВСЕГО	1710

Заданная продолжительность выполнения всего комплекса производственных работ – 21 сутки.

Цель:Определить минимальную стоимость комплекса производственных работ при заданной продолжительности его выполнения и других указанных условиях.

Введение

Сетевое планирование – метод управления, основанный на использовании математического аппарата теории графов и системного подхода для отображения и алгоритмизации комплексов взаимосвязанных работ, действий или мероприятий для достижения четко поставленной цели.

Основная цель сетевого планирования - сокращение до минимума продолжительности проекта.

Задача сетевого планирования состоит в том, чтобы графически, наглядно и системно отобразить и оптимизировать последовательность и взаимозависимость работ, действий или мероприятий, обеспечивающих своевременное и планомерное достижение конечных целей. Для отображения и алгоритмизации тех или иных действий или ситуаций используются экономико-математические модели, которые принято называть сетевыми моделями, простейшие из них - сетевые графики. С помощью сетевой модели руководитель работ или операции имеет возможность системно и масштабно представлять весь ход работ или оперативных мероприятий, управлять процессом их осуществления, а также маневрировать ресурсами.

Таким образом, методы сетевого моделирования относятся к методам принятия оптимальных решений, что оправдывает рассмотрение этого типа моделей в данной курсовой работе.

Целью данной курсовой работы является определение минимальной стоимости комплекса производственных работ при заданной продолжительности работ. Для достижения поставленной цели необходимо решить следующие задачи:

построить сетевой график;
проанализировать сетевой график;
провести оптимизацию сетевого графика.

Построение сетевого графика

В построенном сетевом графике должно быть 6 событий-вершин и 7 работ-дуг.

Построение сетевого графика производится по первой таблице исходных данных.

В этой таблице в шапках по горизонтали и вертикали перечисляются все события, в остальной части таблицы приводятся работы.

Начальным событием– истоком I является«начало работ», а завершающим событием– стоком S – «готовность изделия». Поэтому нужно пронумеровать их соответственно числами 1 и 6.

События (предки)	начало работ (1)	готовность деталей	готовность документации	поступление дополнительного оборудования	готовность блоков
События (потомки)	начало работ (1)	готовность деталей	готовность документации	поступление дополнительного оборудования	готовность блоков
готовность деталей	изготовление деталей (4/3)
готовность документации		подготовка документации (5/2)		установка дополнительного оборудования (12/6)	составление инструкций (11/6)
поступление дополнительного оборудования	закупка дополнительного оборудования (10/5)
готовность блоков		сборка блоков (6/4)
готовность изделия (6)			компоновка изделия (9/6)

Из таблицы видно, что событие 1 (по горизонтали) является началом двух работ-дуг, завершающихся в событиях (по вертикали). Их обозначим по порядку 2 и 3. Те же события по горизонтали обозначаются теми же числами 2 и 3.

События (предки)	начало работ (1)	готовность деталей (2)	готовность документации	поступление дополнительного оборудования (3)	готовность блоков
События (потомки)	начало работ (1)	готовность деталей (2)	готовность документации	поступление дополнительного оборудования (3)	готовность блоков
готовность деталей (2)	изготовление деталей (4/3)
готовность документации		подготовка документации (5/2)		установка дополнительного оборудования (12/6)	составление инструкций (11/6)
поступление дополнительного оборудования (3)	закупка дополнительного оборудования (10/5)
готовность блоков		сборка блоков (6/4)
готовность изделия (6)			компоновка изделия (9/6)

Из события 2 (по горизонтали) выходят две работы-дуги, которые ведут к соответствующим событиям по вертикали. Их обозначим по порядку 4 и 5. Соответствующим событиям по горизонтали присвоим те же числа.

События (предки)	начало работ (1)	готовность деталей (2)	готовность документации (4)	поступление дополнительного оборудования (3)	готовность блоков (5)
События (потомки)	начало работ (1)	готовность деталей (2)	готовность документации (4)	поступление дополнительного оборудования (3)	готовность блоков (5)
готовность деталей (2)	изготовление деталей (4/3)
готовность документации (4)		подготовка документации (5/2)		установка дополнительного оборудования (12/6)	составление инструкций (11/6)
поступление дополнительного оборудования (3)	закупка дополнительного оборудования (10/5)
готовность блоков (5)		сборка блоков (6/4)
готовность изделия (6)			компоновка изделия (9/6)

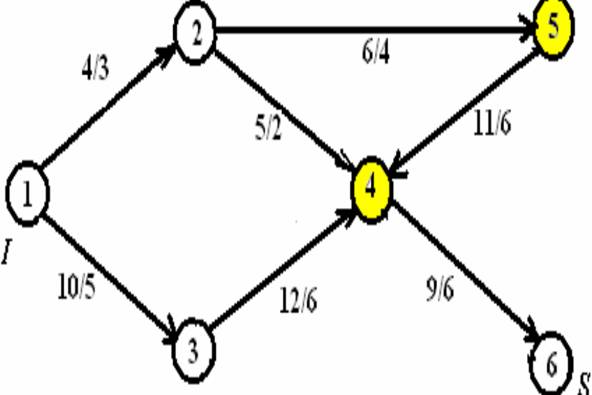
Таким образом, у нас оказались пронумерованы все события. Используя эту нумерацию, а также указанные веса дуг, построим график.

Полученный график оказался неупорядоченным, т.к. предок5 предшествует по-томку4 (5<4). Поэтому эти числа необходимо поменять местами, чтобы получить упорядоченный граф – сетевой график.

Тогда получим окончательный сетевой график.

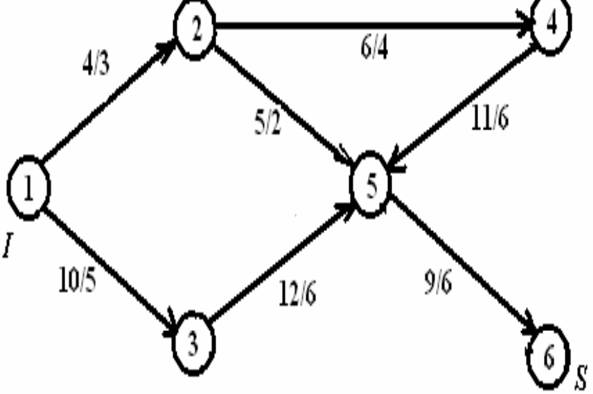
Используя полученную нумерацию событий в графике, получим вторую таблицу

исходных данных в задании. Она примет вид:

Работы	Нормальный вариант		Ускоренный вариант			Прирост затрат на одни сутки ускорения
Работы	Время (сутки)	Затраты (у.е.)		Время (сутки)	Затраты (у.е.)	Прирост затрат на одни сутки ускорения
1-2	4	100		3	120	20
1-3	10	150		5	225	15
2-4	6	50		4	100	25
2-5	5	70		2	100	10
3-5	12	250		6	430	30
4-5	11	260		6	435	35
5-6	9	180		6	300	40
	ВСЕГО	1060		ВСЕГО	1710

2. Анализ сетевого графика

Проведем анализ сетевого графика:

Полные пути	Продолжительность (сутки)
Полные пути	Нормальный режим	Ускоренный режим
1-2-5-6	18	11
1-2-4-5-6	30	19
1-3-5-6	31	17

3. Оптимизация сетевого графика

Требуется оптимизировать по критерию минимизации затрат сетевой график, при заданной продолжительности выполнения всего комплекса работ за 21 сутки.

Представим алгоритм решения поставленной оптимизационной задачи первым способом (нормальный вариант выполнения комплекса работ) в таблице:

№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	Продолжительность полного пути			Общий прирост затрат
№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	1-2-5-6	1-2-4-5-6	1-3-5-6	Общий прирост затрат
0	-	-	-	18	30	31	-
1	10	2-5	(3)
2	15	1-3	(5)
3	20	1-2	(1)
4	25	2-4	(2)
5	30	3-5	(6)
6	35	4-5	(5)
7	40	5-6	(3)
В С Е Г О

В этой таблице работы расположены в порядке возрастания суточного прироста затрат на изменение(снижение) их продолжительности. Наименования полных путей и их продолжительность взяты из результатов предыдущего анализа сетевого графика для рассматриваемого нормального варианта. Максимально возможное количество сокращаемых суток для каждой работы указано в скобках.

На первом шаге рассматривается работа 2-5, которая входит в первый полный путь

и ее продолжительность сокращать не нужно, т.к. продолжительность первого полного

пути меньше требуемой:

№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	Продолжительность полного пути			Общий прирост затрат
№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	1-2-5-6	1-2-4-5-6	1-3-5-6	Общий прирост затрат
0	-	-	-	18	30	31	-
1	10	2-5	(3) -	-	-	-	-
2	15	1-3	(5)
3	20	1-2	(1)
4	25	2-4	(2)
5	30	3-5	(6)
6	35	4-5	(5)
7	40	5-6	(3)
В С Е Г О

Аналогично рассматривается возможность снижения продолжительности работы 1-3 на втором шаге:

№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	Продолжительность полного пути			Общий прирост затрат
№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	1-2-5-6	1-2-4-5-6	1-3-5-6	Общий прирост затрат
0	-	-	-	18	30	31	-
1	10	2-5	(3) -	-	-	-	-
2	15	1-3	(5) 5	-	-	26	75
3	20	1-2	(1)
4	25	2-4	(2)
5	30	3-5	(6)
6	35	4-5	(5)
7	40	5-6	(3)
В С Е Г О

Работа 1-3 входит в третий полный путь и ее продолжительность может быть сокращена на максимально возможную величину (указано в скобках), т.к. при этом продолжительность третьего полного пути все равно будет выше требуемой(31-5=26>21), а следовательно, и весь комплекс работ будет выполнен за большее количество суток, чем задано. Указанное сокращение продолжительности этой работы приведет к дополнительным затратам, величина которых рассчитывается как произведение количества сокращаемых суток на стоимость суточного прироста затрат: 5х15=75. Эта величина учитывается в таблице в общем приросте затрат.

Работа 1-2, соответствующая третьему шагу, входит в первый и второй полные пути. Она может быть сокращена на максимально возможную величину(указано в скобках), т.к. при этом продолжительность второго полного пути все равно будет выше требуемой (30-1=29>21), а следовательно, и весь комплекс работ будет выполнен за большее количество суток, чем задано. И это несмотря на то, что продолжительность первого полного пути сокращения не требовала. Затраты на такое сокращение рассчитываются аналогично: 1х20=20.

№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	Продолжительность полного пути			Общий прирост затрат
№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	1-2-5-6	1-2-4-5-6	1-3-5-6	Общий прирост затрат
0	-	-	-	18	30	31	-
1	10	2-5	(3) -	-	-	-	-
2	15	1-3	(5) 5	-	-	26	75
3	20	1-2	(1) 1	17	29	-	20
4	25	2-4	(2)
5	30	3-5	(6)
6	35	4-5	(5)
7	40	5-6	(3)
В С Е Г О

На четвертом шаге стоит работа 2-4, которая входит во второй полный путь. Сокращение ее продолжительности производится по максимуму на 2 суток, т.к. и это не позволяет довести продолжительность всего комплекса работ до требуемой: 29-2=27>21.

Также рассчитываются затраты на такое сокращение: 2х25=50.

№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	Продолжительность полного пути			Общий прирост затрат
№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	1-2-5-6	1-2-4-5-6	1-3-5-6	Общий прирост затрат
0	-	-	-	18	30	31	-
1	10	2-5	(3) -	-	-	-	-
2	15	1-3	(5) 5	-	-	26	75
3	20	1-2	(1) 1	17	29	-	20
4	25	2-4	(2) 2	-	27	-	50
5	30	3-5	(6)
6	35	4-5	(5)
7	40	5-6	(3)
В С Е Г О

Сокращение продолжительности работы3-5 на пятом шаге производится только на 5 суток(из6 возможных), т.к. при этом продолжительность третьего полного пути, в который она входит, становится равной заданной: 26-5=21. Аналогично рассчитываются затраты на такое сокращение: 5х30=150.

№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	Продолжительность полного пути			Общий прирост затрат
№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	1-2-5-6	1-2-4-5-6	1-3-5-6	Общий прирост затрат
0	-	-	-	18	30	31	-
1	10	2-5	(3) -	-	-	-	-
2	15	1-3	(5) 5	-	-	26	75
3	20	1-2	(1) 1	17	29	-	20
4	25	2-4	(2) 2	-	27	-	50
5	30	3-5	(6) 5	-	-	21	150
6	35	4-5	(5)
7	40	5-6	(3)
В С Е Г О

А на шестом шаге сокращение продолжительности работы4-5 осуществляется по максимуму(27-5=22) и рассчитываются затраты на это сокращение(5х35=175), т.к. она входит во второй полный путь, определяющий продолжительность всего комплекса работ и не достигающий заданного значения.

№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	Продолжительность полного пути			Общий прирост затрат
№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	1-2-5-6	1-2-4-5-6	1-3-5-6	Общий прирост затрат
0	-	-	-	18	30	31	-
1	10	2-5	(3) -	-	-	-	-
2	15	1-3	(5) 5	-	-	26	75
3	20	1-2	(1) 1	17	29	-	20
4	25	2-4	(2) 2	-	27	-	50
5	30	3-5	(6) 5	-	-	21	150
6	35	4-5	(5) 5	-	22	-	175
7	40	5-6	(3)
В С Е Г О

На седьмом шаге уменьшение продолжительности работы 5-6, входящей во все полные пути, определяется продолжительностью более критичного второго полного пути, соответствующей продолжительности всего комплекса работ. Поэтому эта продолжительность уменьшается на 1 сутки и тем самым достигается заданная продолжительность всего комплекса работ (22-1=21). Затраты на это тоже пропорциональны 1 суткам (1х40=40).

№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	Продолжительность полного пути			Общий прирост затрат
№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	1-2-5-6	1-2-4-5-6	1-3-5-6	Общий прирост затрат
0	-	-	-	18	30	31	-
1	10	2-5	(3) -	-	-	-	-
2	15	1-3	(5) 5	-	-	26	75
3	20	1-2	(1) 1	17	29	-	20
4	25	2-4	(2) 2	-	27	-	50
5	30	3-5	(6) 5	-	-	21	150
6	35	4-5	(5) 5	-	22	-	175
7	40	5-6	(3) 1	16	21	20	40
В С Е Г О							510

Подсчитываются суммарные дополнительные затраты на произведенное сокращение продолжительностей работ (75+20+50+150+175+40=510 у.е.).

Анализируются полученные результаты на их оптимальность. Равна заданной только продолжительность второго полного пути, а продолжительности остальных полных путей меньше заданной, поэтому нужно проанализировать их изменения. Продолжительность первого полного пути меньше заданной, но ее нельзя увеличить, т.к. при этом увеличится продолжительность второго полного пути, равная заданной. Продолжительность третьего полного пути также меньше заданной, но ее можно увеличить на шагах 2 и 5, т.к. это не связано с увеличением продолжительности других путей. Изменим продолжительность этого полного пути на5 шаге как наиболее дорогом, а, следовательно, соответствующем наибольшему уменьшению стоимости всего комплекса работ.

№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	Продолжительность полного пути			Общий прирост затрат
№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	1-2-5-6	1-2-4-5-6	1-3-5-6	Общий прирост затрат
0	-	-	-	18	30	31	-
1	10	2-5	(3) -	-	-	-	-
2	15	1-3	(5) 5	-	-	26	75
3	20	1-2	(1) 1	17	29	-	20
4	25	2-4	(2) 2	-	27	-	50
5	30	3-5	(6) 4	-	-	22	120
6	35	4-5	(5) 5	-	22	-	175
7	40	5-6	(3) 1	16	21	21	40
В С Е Г О							480

Теперь подсчитав суммарные дополнительные затраты на произведенное сокращение продолжительностей работ (480 у.е.) и зная первоначальную стоимость (1060 у.е.) всего комплекса работ в рассматриваемом нормальном варианте его выполнения(см. вторую таблицу исходных данных), получим, что при снижении продолжительности выполнения всего комплекса работ с 31 суток(критический путь) до 21 суток оптимальные затраты составят 1060+480=1540 (у.е.).

Представим алгоритм решения поставленной оптимизационной задачи вторым способом (ускоренный вариант выполнения комплекса работ) в таблице:

№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	Продолжительность полного пути			Общий прирост затрат
№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	1-2-5-6	1-2-4-5-6	1-3-5-6	Общий прирост затрат
0	-	-	-	11	19	17	-
1	40	5-6	(3)
2	35	4-5	(5)
3	30	3-5	(6)
4	25	2-4	(2)
5	20	1-2	(1)
6	15	1-3	(5)
7	10	2-5	(3)
В С Е Г О

Отличие этой таблицы от предыдущей состоит в том, что в ней работы располагаются в порядке убывания их суточного прироста затрат на изменение(увеличение) их продолжительности. Продолжительность полных путей здесь взята из результатов предыдущего анализа сетевого графика для рассматриваемого ускоренного варианта выполнения всего комплекса работ. В последней колонке теперь будет рассчитываться уже снижение затрат.

На первом шаге продолжительность работы 5-6 может быть увеличена только на 2 суток, т.к. при этом продолжительность второго полного пути станет как требуемая в задании.

№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	Продолжительность полного пути			Общий прирост затрат
№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	1-2-5-6	1-2-4-5-6	1-3-5-6	Общий прирост затрат
0	-	-	-	11	19	17	-
1	40	5-6	(3) 2	13	21	19	-80
2	35	4-5	(5)
3	30	3-5	(6)
4	25	2-4	(2)
5	20	1-2	(1)
6	15	1-3	(5)
7	10	2-5	(3)
В С Е Г О

Тогда затраты на эту работу, с более поздним сроком выполнения, снизятся на 2·40=80 (у.е.), т.е. -80 у.е.

Второй шаг придется не использовать, т.к. увеличение продолжительности соответствующей ему работы 4-5 приведет к недопустимому увеличению продолжительности второго полного пути, а следовательно, и всего комплекса работ.

№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	Продолжительность полного пути			Общий прирост затрат
№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	1-2-5-6	1-2-4-5-6	1-3-5-6	Общий прирост затрат
0	-	-	-	11	19	17	-
1	40	5-6	(3) 2	13	21	19	-80
2	35	4-5	(5) -	-	-	-	-
3	30	3-5	(6)
4	25	2-4	(2)
5	20	1-2	(1)
6	15	1-3	(5)
7	10	2-5	(3)
В С Е Г О

Рассматривая работу 3-5 на третьем шаге, приходим к выводу, что ее продолжительность можно увеличить на 2 суток, т.к. при этом продолжительность третьего полного пути станет как требуемая в задании, а остальных путей– не изменится.

№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	Продолжительность полного пути			Общий прирост затрат
№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	1-2-5-6	1-2-4-5-6	1-3-5-6	Общий прирост затрат
0	-	-	-	11	19	17	-
1	40	5-6	(3) 2	13	21	19	-80
2	35	4-5	(5) -	-	-	-	-
3	30	3-5	(6) 2	-	-	21	-60
4	25	2-4	(2)
5	20	1-2	(1)
6	15	1-3	(5)
7	10	2-5	(3)
В С Е Г О

Затраты на эту работу, с более поздним сроком выполнения, снизятся на 2·30=60

(у.е.), т.е. -60 у.е.

Четвертый, пятый и шестой шаги пропускаем по той же причине, что и второй шаг.

№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	Продолжительность полного пути			Общий прирост затрат
№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	1-2-5-6	1-2-4-5-6	1-3-5-6	Общий прирост затрат
0	-	-	-	11	19	17	-
1	40	5-6	(3) 2	13	21	19	-80
2	35	4-5	(5) -	-	-	-	-
3	30	3-5	(6) 2	-	-	21	-60
4	25	2-4	(2) -	-	-	-	-
5	20	1-2	(1) -	-	-	-	-
6	15	1-3	(5) -	-	-	-	-
7	10	2-5	(3)
В С Е Г О

На последнем седьмом шаге продолжительность работы 2-5 может быть увеличена на максимально возможную величину в 3 суток, т.к. при этом продолжительность первого полного пути станет больше, хотя и не достигнет требуемой в задании, но приведет к уменьшению стоимости всего комплекса работ.

№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	Продолжительность полного пути			Общий прирост затрат
№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	1-2-5-6	1-2-4-5-6	1-3-5-6	Общий прирост затрат
0	-	-	-	11	19	17	-
1	40	5-6	(3) 2	13	21	19	-80
2	35	4-5	(5) -	-	-	-	-
3	30	3-5	(6) 2	-	-	21	-60
4	25	2-4	(2) -	-	-	-	-
5	20	1-2	(1) -	-	-	-	-
6	15	1-3	(5) -	-	-	-	-
7	10	2-5	(3) 3	16	-	-	-30
В С Е Г О							-170

Подсчитав суммарное снижение затрат из-за произведенного увеличения продолжительностей работ (-80-60-30=-170 у.е.) и зная первоначальную стоимость(1710 у.е.) всего комплекса работ в рассматриваемом ускоренном варианте его выполнения(см. вторую таблицу исходных данных), получим, что при увеличении продолжительности выполнения всего комплекса работ с 19 суток (критический путь) до 21 суток оптимальные затраты составят 1710-170=1540 (у.е.).

Итоговые результаты, полученные обоими способами оптимизации, должны совпадать. Проверим это:

1) продолжительности соответствующих полных путей после оптимизации

совпадают– 16,21,21;

2) стоимости выполнения всего комплекса работ после оптимизации совпадают – 1540.

Заключение

В данной курсовой работе был построен сетевой график, проведен его анализ. Произведена оптимизация сетевого графика. При использовании данных методик можно найти критический путь сетевого графика. В результате оптимизации определили минимальную стоимость комплекса работ при заданной продолжительности его выполнения:

· при снижении продолжительности выполнения всего комплекса работ с 31 суток (критический путь) до 21 суток оптимальные затраты составят 1540 (у.е.).

· при увеличении продолжительности выполнения всего комплекса работ с 19 суток (критический путь) до 21 суток оптимальные затраты составят 1540 (у.е.).

Список использованной литературы

Абланская Л.В., Бабешко Л.О., Баусов Л.И. Экономико-математическое моделирование: М.: Экзамен, 2006г. – 800с.
Баканов М.И., Шеремет А.Д. Теория экономического анализа: Учебник. - М.: Финансы и статистика, 1997.
Дрогобыцкого И.Н Экономико-математическое моделирование: М.: Экзамен, 2004г. – 323с.
Казаков О.Л., Миненко С.Н., Смирнов Г.Б. Экономико-математическое моделирование: учебно-методическое пособие. – М.: МГИУ, 2006. - 136 с.
Конюховский П.В Математические методы исследования операций в экономике: С-Петербург: Питер 2003г. - 208 с.

Оптимизация сетевой модели по критерию затраты

Введение

Построение сетевого графика

2. Анализ сетевого графика

3. Оптимизация сетевого графика

Заключение

Список использованной литературы

Правила ввода данных

Поиск

Процесс

Сообщение