Пример построения сетевого графика
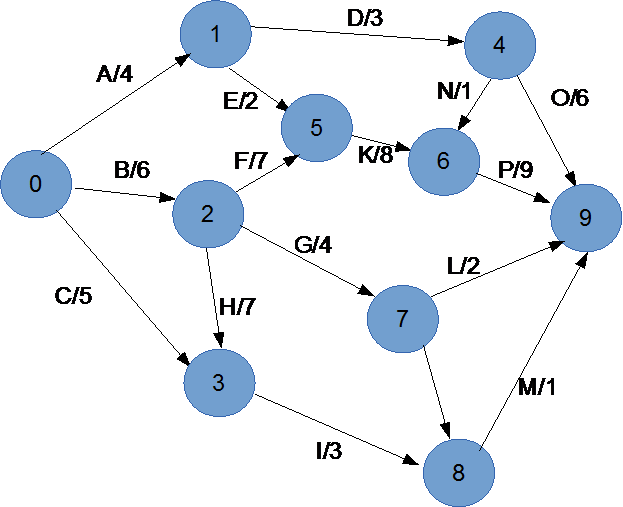
В одной из фирм решили внедрить систему компьютерной информации. Назначенный руководитель проекта составил список действий (работ), которые надо для этого выполнить, и указал последовательность их выполнения и продолжительность, приведенную в таблице. Постройте сетевой график.Указание:
a) в сети должно быть одно исходное и одно завершающее событие;
b) присмотревшись к перечню работ, вы обнаружите, что работы А, В и С не имеют
предшествующих работ (у них только последующие), значит, их можно выполнять
параллельно, начиная от исходного события;
c) избегайте пересечения путей;
d) направляйте работы слева направо;
e) на графике должно быть как можно меньше фиктивных работ.
| Работа | Продолжительность работы t, дн. | Последующая работа |
| A | 4 | D, E |
| D | 3 | O, N |
| O | 6 | Конец |
| E | 2 | K |
| K | 8 | P |
| N | 1 | P |
| P | 9 | Конец |
| B | 6 | F, G, H |
| F | 7 | K |
| G | 4 | L, M |
| L | 2 | Конец |
| C | 5 | I |
| H | 7 | I |
| I | 3 | M |
| M | 1 | Конец |
Далее можно будет найти параметры сетевого графика.
Масштабный сетевой график
Рассчитать параметры сетевого графика мероприятия по совершенствованию системы управления. Сетевая модель задана таблично (Таблица). Продолжительность выполнения работ дана в виде минимальной и максимальной оценок. Требуется:- Вычислить табличным методом все основные характеристики работ и событий, найти критический путь и его продолжительность.
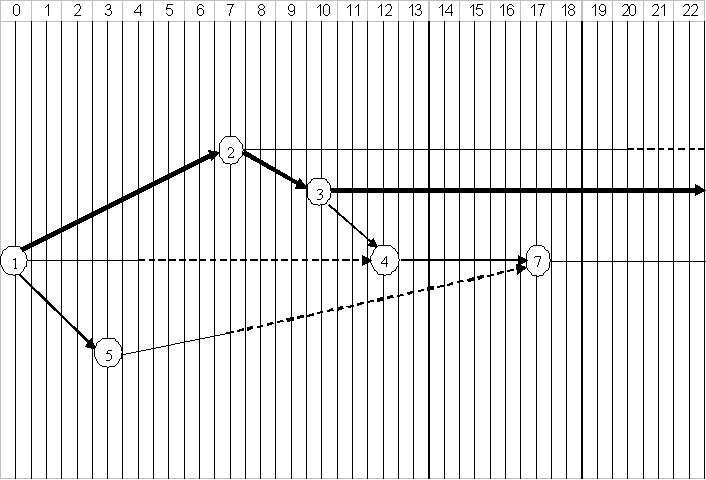
- Построить масштабный сетевой график.
- Оценить вероятность выполнения всего комплекса работ за 30 дней.
- Оценить максимально возможный срок выполнения всего комплекса работ с вероятностью 95%.
Таблица - Сетевая модель.
| Код работы ( i,j) | Продолжительность | |
tmin (i,j) | tmax (i,j) | |
| 1,2 | 5 | 10 |
| 1,4 | 2 | 7 |
| 1,5 | 1 | 6 |
| 2,3 | 2 | 4,5 |
| 2,8 | 9 | 19 |
| 3,4 | 1 | 3,5 |
| 3,6 | 9 | 19 |
| 4,7 | 4 | 6,5 |
| 5,7 | 2 | 7 |
| 6,8 | 7 | 12 |
| 7,8 | 5 | 7,5 |
Решение находим с помощью сервиса Сетевая модель
. В нашем задании продолжительность выполнения работы задаётся двумя оценками – минимальная и максимальная. Минимальная оценка характеризует продолжительность выполнения работы при наиболее благоприятных обстоятельствах, а максимальная tmax(i,j) – при наиболее неблагоприятных условиях. Продолжительность работы в этом случае рассматривается, как случайная величина, которая в результате реализации может принять любое значение в заданном интервале. Такие оценки называются вероятностными (случайными), и их ожидаемое значение tож(i,j) оценивается по формуле
tож(i,j)=(3 tmin(i,j)+2 tmax (i,j))/5
Для характеристики степени разброса возможных значений вокруг ожидаемого уровня используется показатель дисперсии:
S2(i,j)=0,04(tmax(i,j)-tmin(i,j))2
Рассчитаем ожидаемое значение и показатель дисперсии.
tож(1,2)=(3*5+2*10)/5=7
tож(1,4)=(3*2+2*7)/5=4
tож(1,5)=(3*1+2*6)/5=3
tож(2,3)=(3*2+2*4,5)/5=3
tож(2,8)=(3*9+2*19)/5=13
tож(3,4)=(3*1+2*3,5)/5=2
tож(3,6)=(3*9+2*19)/5=13
tож(4,7)=(3*4+2*6,5)/5=5
tож(5,7)=(3*2+2*7)/5=4
tож(6,8)=(3*7+2*12)/5=9
tож(7,8)=(3*5+2*7,5)/5=6
S2(1,2)=0,04*(10-5)2=1
S2(1,4)=0,04*(7-2)2=1
S2(1,5)=0,04*(6-1)2=1
S2(2,3)=0,04*(4,5-1)2=0,25
S2(2,8)=0,04*(19-9)2=4
S2(3,4)=0,04*(3,5-1)2=6,25
S2(3,6)=0,04*(19-9)2=4
S2(4,7)=0,04*(6,5-4)2=0,25
S2(5,7)=0,04*(7-2)2=1
S2(6,8)=0,04*(12-7)2=1
S2(7,8)=0,04*(7,5-5)2=0,25
Полученные данные занесем в таблицу.
Таблица – Сетевая модель.
| Работа ( i,j) | Продолжительность | Ожидаемая продолжительность tож(i,j) | Дисперсия S2(i,j) | |
tmin (i,j) | tmax (i,j) | |||
| 1,2 | 5 | 10 | 7 | 1 |
| 1,4 | 2 | 7 | 4 | 1 |
| 1,5 | 1 | 6 | 3 | 1 |
| 2,3 | 2 | 4,5 | 3 | 0,25 |
| 2,8 | 9 | 19 | 13 | 4 |
| 3,4 | 1 | 3,5 | 2 | 6,25 |
| 3,6 | 9 | 19 | 13 | 4 |
| 4,7 | 4 | 6,5 | 5 | 0,25 |
| 5,7 | 2 | 7 | 4 | 1 |
| 6,8 | 7 | 12 | 9 | 1 |
| 7,8 | 5 | 7,5 | 6 | 0,25 |
Используя полученные данные, мы можем найти основные характеристики сетевой модели табличным методом, критический путь и его продолжительность.
Таблица – Табличный метод расчета сетевого графика.
| КПР | Код работы (i,j) | Продолжительность работы t(i, j) | Ранние сроки | Поздние сроки | Резервы времени | |||
| tрн(i,j) | tро(i,j) | tпн(i,j) | tпо(i,j) | Rп | Rc | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 1,2 | 7 | 0 | 7 | 0 | 7 | 0 | 0 |
| 0 | 1,4 | 4 | 0 | 4 | 17 | 21 | 17 | 8 |
| 0 | 1,5 | 3 | 0 | 3 | 19 | 22 | 19 | 0 |
| 1 | 2,3 | 3 | 7 | 10 | 7 | 10 | 0 | 0 |
| 1 | 2,8 | 13 | 7 | 20 | 19 | 32 | 12 | 12 |
| 1 | 3,4 | 2 | 10 | 12 | 19 | 21 | 9 | 0 |
| 1 | 3,6 | 13 | 10 | 23 | 10 | 23 | 0 | 0 |
| 2 | 4,7 | 5 | 12 | 17 | 21 | 26 | 9 | 0 |
| 1 | 5,7 | 4 | 3 | 7 | 22 | 26 | 19 | 10 |
| 1 | 6,8 | 9 | 23 | 32 | 23 | 32 | 0 | 0 |
| 2 | 7,8 | 6 | 17 | 23 | 26 | 32 | 9 | 9 |
Для оценки вероятности выполнения всего комплекса работ за 30 дней нам необходима следующая формула:
Z- нормативное отклонение случайной величины, Sкр – среднеквадратическое отклонение, вычисляемое как корень квадратный из дисперсии продолжительности критического пути. Соответствие между Z и Ф(Z) представлено в таблице.
Таблица - Таблица стандартного нормального распределения.
| Z | F(Z) | Z | F(Z) | Z | F(Z) |
| 0 | 0.0000 | 1.0 | 0.6827 | 2.0 | 0.9643 |
| 0.1 | 0.0797 | 1.1 | 0.7287 | 2.1 | 0.9722 |
| 0.2 | 0.1585 | 1.2 | 0.7699 | 2.2 | 0.9786 |
| 0.3 | 0.2358 | 1.3 | 0.8064 | 2.3 | 0.9836 |
| 0.4 | 0.3108 | 1.4 | 0.8385 | 2.4 | 0.9876 |
| 0.5 | 0.3829 | 1.5 | 0.8664 | 2.5 | 0.9907 |
| 0.6 | 0.4515 | 1.6 | 0.8904 | 2.6 | 0.9931 |
| 0.7 | 0.5161 | 1.7 | 0.9104 | 2.7 | 0.9949 |
| 0.8 | 0.5763 | 1.8 | 0.9281 | 2.8 | 0.9963 |
| 0.9 | 0.6319 | 1.9 | 0.9545 | 2.9 | 0.9973 |
Дисперсия критического пути:
S2(Lкр)= S2(1,2)+ S2(2,3)+ S2(3,6)+S2(6,8)=1+0,25+4+1=6,25
S(Lкр)=2,5
p(tкр<30)=0,5+0,5Ф((30-32)/2,5)=0,5-0,5Ф(0,8) = 0,5-0,5*0,5763=0,5-0,28815=0,213
Вероятность того, что весь комплекс работ будет выполнен не более чем за 30 дней, составляет 21,3%.
Для определения максимально возможного срока выполнения всего комплекса работ с надежностью 95% будем использовать следующую формулу:
Для решения поставленной задачи найдем значение аргумента Z, которое соответствует заданной вероятности 95% (значению графы Ф(Z) 0,9545*100% в таблице 5 соответствует Z=1,9).
T=32+1,9*2,5=36,8
Максимальный срок выполнения всего комплекса работ при заданном уровне вероятности 95% составляет всего 36,8 дня.

