Коэффициент напряженности
Коэффициентом напряженности КH работы Pi,j называется отношение продолжительности несовпадающих (заключенных между одними и теми же событиями) отрезков пути, одним из которых является путь максимальной продолжительности, проходящий через данную работу, а другим – критический путь: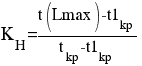
где t(Lmax) – продолжительность максимального пути, проходящего через работу Pi,j, от начала до конца сетевого графика; tkp – продолжительность (длина) критического пути; t1kp – продолжительность отрезка рассматриваемого максимального пути, совпадающего с критическим путем.
Коэффициент напряженности КH работы Pi,j может изменяться в пределах от 0 (для работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности) до 1 (для работ критического пути). Чем ближе к 1 коэффициент напряженности КH работы Pi,j, тем сложнее выполнить данную работу в установленные сроки. Чем ближе Кн работы Pi,j к нулю, тем большим относительным резервом обладает максимальный путь, проходящий через данную работу.
Вычисленные коэффициенты напряженности позволяют дополнительно классифицировать работы по зонам. В зависимости от величины Кн выделяют три зоны: критическую (Кн > 0,8); подкритическую (0,6 < Кн < 0,8); резервную (Кн < 0,6).
Пример. Предположим, что при составлении некоторого проекта выделено 12 событий: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 и 24 связывающие их работы: (0-1), (0-3), (0-5), (1-2), (1-3), (1-4), (2-7), (3-4), (3-5), (3-6), (4-6), (4-7), (5-6), (5-8), (5-9), (6-7), (6-8), (6-9), (6-10), (7-10), (8-9), (9-10), (9-11), (10-11). Необходимо:
1) составить и упорядочить сетевой график;
2) определить временные параметры сетевого графика;
3) оценить вероятность выполнения проекта в установленный срок;
4) оптимизировать сетевой график методом «время-стоимость».
Продолжительность работы в этом случае рассматривается, как случайная величина, которая в результате реализации может принять любое значение в заданном интервале. Такие оценки называются вероятностными (случайными), и их ожидаемое значение tож(i,j) оценивается по формуле:
tож(i,j)=(tmin(i,j)+4m(i,j)+tmax(i,j))/6
Для характеристики степени разброса возможных значений вокруг ожидаемого уровня используется показатель дисперсии:
S2(i,j)=1/36 (tmax(i,j)-tmin(i,j))2
Рассчитаем ожидаемое значение и показатель дисперсии.
tож(1,2)=(2+4*9+10)/6=8
tож(1,4)=(14+4*12+16)/6=13
tож(1,6)=(2+4*10+12)/6=9
tож(2,3)=(1+4*10+13)/6=9
tож(2,5)=(4+4*5+12)/6=6
tож(2,4)=(2+4*3+10)/6=4
tож(3,8)=(2+4*3+4)/6=3
tож(4,5)=(5+4*9+19)/6=10
tож(4,6)=(1+4*8+9)/6=7
tож(4,7)=(3+4*6+9)/6=6
tож(5,8)=(2+4*9+10)/6=8
tож(5,7)=(2+4*3+4)/6=3
tож(6,7)=(2+4*10+12)/6=9
tож(6,9)=(6+4*9+18)/6=10
tож(6,10)=(4+4*5+12)/6=6
tож(7,8)=(1+4*4+7)/6=4
tож(7,11)=(4+4*5+6)/6=5
tож(7,10)=(14+4*12+16)/6=13
tож(7,9)=(7+4*8+9)/6=8
tож(8,11)=(2+4*5+8)/6=5
tож(9,10)=(3+4*4+5)/6=4
tож(10,11)=(5+4*6+7)/6=6
tож(10,12)=(5+4*19+21)/6=17
tож(11,12)=(14+4*11+20)/6=13
S2(1,2)=1/36(10-2)2=1.78
S2(1,4)=1/36(16-14)2=0.11
S2(1,6)=1/36(12-2)2=2.78
S2(2,3)=1/36(13-1)2=4
S2(2,5)=1/36(12-4)2=1.78
S2(2,4)=1/36(10-2)2=1.78
S2(3,8)=1/36(4-2)2=0.11
S2(4,5)=1/36(19-5)2=5.44
S2(4,6)=1/36(9-1)2=1.78
S2(4,7)=1/36(9-3)2=1
S2(5,8)=1/36(10-2)2=1.78
S2(5,7)=1/36(4-2)2=0.11
S2(6,7)=1/36(12-2)2=2.78
S2(6,9)=1/36(18-6)2=4
S2(6,10)=1/36(12-4)2=1.78
S2(7,8)=1/36(7-1)2=1
S2(7,11)=1/36(6-4)2=0.11
S2(7,10)=1/36(16-14)2=0.11
S2(7,9)=1/36(9-7)2=0.11
S2(8,11)=1/36(8-2)2=1
S2(9,10)=1/36(5-3)2=0.11
S2(10,11)=1/36(7-5)2=0.11
S2(10,12)=1/36(21-5)2=7.11
S2(11,12)=1/36(20-14)2=1
Полученные данные занесем в таблицу.
| Работа (i,j) | tmin(i,j) | tmax(i,j) | m(i,j) | Ожидаемая продолжительность tож(i,j) | Дисперсия S2(i,j) |
| 1,2 | 2 | 10 | 9 | 8 | 1.78 |
| 1,4 | 14 | 16 | 12 | 13 | 0.11 |
| 1,6 | 2 | 12 | 10 | 9 | 2.78 |
| 2,3 | 1 | 13 | 10 | 9 | 4 |
| 2,5 | 4 | 12 | 5 | 6 | 1.78 |
| 2,4 | 2 | 10 | 3 | 4 | 1.78 |
| 3,8 | 2 | 4 | 3 | 3 | 0.11 |
| 4,5 | 5 | 19 | 9 | 10 | 5.44 |
| 4,6 | 1 | 9 | 8 | 7 | 1.78 |
| 4,7 | 3 | 9 | 6 | 6 | 1 |
| 5,8 | 2 | 10 | 9 | 8 | 1.78 |
| 5,7 | 2 | 4 | 3 | 3 | 0.11 |
| 6,7 | 2 | 12 | 10 | 9 | 2.78 |
| 6,9 | 6 | 18 | 9 | 10 | 4 |
| 6,10 | 4 | 12 | 5 | 6 | 1.78 |
| 7,8 | 1 | 7 | 4 | 4 | 1 |
| 7,11 | 4 | 6 | 5 | 5 | 0.11 |
| 7,10 | 14 | 16 | 12 | 13 | 0.11 |
| 7,9 | 7 | 9 | 8 | 8 | 0.11 |
| 8,11 | 2 | 8 | 5 | 5 | 1 |
| 9,10 | 3 | 5 | 4 | 4 | 0.11 |
| 10,11 | 5 | 7 | 6 | 6 | 0.11 |
| 10,12 | 5 | 21 | 19 | 17 | 7.11 |
| 11,12 | 14 | 20 | 11 | 13 | 1 |
Решение: все вычисления будем заносить в таблицу.
Перечень работ и их продолжительность перенесем во вторую и третью графы. При этом работы следует записывать в графу 2 последовательно: сначала начиная с номера , затем с номера 1 и т.д.
Во второй графе поставим число, характеризующее количество непосредственно предшествующих работ (КПР) тому событию, с которого начинается рассматриваемая работа.
Так, для работы (3,4) в графу 1 поставим число 2, т.к. на номер 3 оканчиваются 2 работы: (0,3),(1,3).
Далее заполняем графы 4 и 5. Для работ, имеющих цифру 0 в графе 2, в графу 4 также заносятся нули, а их значения в графе 5 получаются в результате суммирования граф 3 и 4.
Для заполнения следующих строк графы 4, т.е. строк начиная с номера 2, просматриваются заполненные строки графы 5, содержащие работы, которые оканчиваются на этот номер, и максимальное значение переносится в графу 4 обрабатываемых строк.
Этот процесс повторяется до тех пор, пока не будет заполнена последняя строка таблицы.
Заполнение графы 4.
Рассмотрим события: (0,1): 8. Заносим значение 8 в графу.
Рассмотрим события: (1,2): 17. Заносим значение 17 в графу.
Рассмотрим события: (0,3): 13;(1,3): 12. Максимальное значение: 13. Заносим его в графу.
Рассмотрим события: (1,4): 14;(3,4): 23. Максимальное значение: 23. Заносим его в графу.
Рассмотрим события: (0,5): 9;(3,5): 20. Максимальное значение: 20. Заносим его в графу.
Рассмотрим события: (3,6): 19;(4,6): 26;(5,6): 29. Максимальное значение: 29. Заносим его в графу.
Рассмотрим события: (2,7): 20;(4,7): 31;(6,7): 33. Максимальное значение: 33. Заносим его в графу.
Рассмотрим события: (5,8): 30;(6,8): 37. Максимальное значение: 37. Заносим его в графу.
Рассмотрим события: (5,9): 26;(6,9): 42;(8,9): 41. Максимальное значение: 42. Заносим его в графу.
Рассмотрим события: (6,10): 34;(7,10): 38;(9,10): 48. Максимальное значение: 48. Заносим его в графу.
Графы 6 и 7 заполняются обратным ходом, т.е. снизу вверх. Для этого просматриваются строки, оканчивающиеся на номер последнего события, и из графы 5 выбирается максимальная величина, которая записывается в графу 7 по всем строчкам, оканчивающимся на номер последнего события (т.к. tр(i)= tп(i)).
Процесс повторяется до тех пор, пока не будут заполнены все строчки по графам 6 и 7.
Заполнение графы 7.
Рассмотрим события:
(9,11): 59
(10,11): 61
Максимальное значение: 61. Записываем его в графу 7 по всем строчкам, оканчивающимся на номер последнего события 11.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 10. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 10.
(10,11): 61 - 13 = 48;
Данное значение переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 48.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 9. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 9.
(9,10): 48 - 6 = 42;
(9,11): 61 - 17 = 44;
В графу 6 среди них выбирается минимальная величина, которая переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 42.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 10. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 10.
(10,11): 61 - 13 = 48;
Данное значение переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 48.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 10. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 10.
(10,11): 61 - 13 = 48;
Данное значение переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 48.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 9. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 9.
(9,10): 48 - 6 = 42;
(9,11): 61 - 17 = 44;
В графу 6 среди них выбирается минимальная величина, которая переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 42.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 8. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 8.
(8,9): 42 - 4 = 38;
Данное значение переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 38.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 7. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 7.
(7,10): 48 - 5 = 43;
Данное значение переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 43.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 9. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 9.
(9,10): 48 - 6 = 42;
(9,11): 61 - 17 = 44;
В графу 6 среди них выбирается минимальная величина, которая переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 42.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 8. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 8.
(8,9): 42 - 4 = 38;
Данное значение переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 38.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 6. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 6.
(6,7): 43 - 4 = 39;
(6,8): 38 - 8 = 30;
(6,9): 42 - 13 = 29;
(6,10): 48 - 5 = 43;
В графу 6 среди них выбирается минимальная величина, которая переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 29.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 7. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 7.
(7,10): 48 - 5 = 43;
Данное значение переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 43.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 6. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 6.
(6,7): 43 - 4 = 39;
(6,8): 38 - 8 = 30;
(6,9): 42 - 13 = 29;
(6,10): 48 - 5 = 43;
В графу 6 среди них выбирается минимальная величина, которая переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 29.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 6. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 6.
(6,7): 43 - 4 = 39;
(6,8): 38 - 8 = 30;
(6,9): 42 - 13 = 29;
(6,10): 48 - 5 = 43;
В графу 6 среди них выбирается минимальная величина, которая переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 29.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 5. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 5.
(5,6): 29 - 9 = 20;
(5,8): 38 - 10 = 28;
(5,9): 42 - 6 = 36;
В графу 6 среди них выбирается минимальная величина, которая переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 20.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 4. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 4.
(4,6): 29 - 3 = 26;
(4,7): 43 - 8 = 35;
В графу 6 среди них выбирается минимальная величина, которая переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 26.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 7. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 7.
(7,10): 48 - 5 = 43;
Данное значение переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 43.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 4. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 4.
(4,6): 29 - 3 = 26;
(4,7): 43 - 8 = 35;
В графу 6 среди них выбирается минимальная величина, которая переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 26.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 3. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 3.
(3,4): 26 - 10 = 16;
(3,5): 20 - 7 = 13;
(3,6): 29 - 6 = 23;
В графу 6 среди них выбирается минимальная величина, которая переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 13.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 2. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 2.
(2,7): 43 - 3 = 40;
Данное значение переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 40.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 5. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 5.
(5,6): 29 - 9 = 20;
(5,8): 38 - 10 = 28;
(5,9): 42 - 6 = 36;
В графу 6 среди них выбирается минимальная величина, которая переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 20.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 3. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 3.
(3,4): 26 - 10 = 16;
(3,5): 20 - 7 = 13;
(3,6): 29 - 6 = 23;
В графу 6 среди них выбирается минимальная величина, которая переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 13.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 1. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 1.
(1,2): 40 - 9 = 31;
(1,3): 13 - 4 = 9;
(1,4): 26 - 6 = 20;
В графу 6 среди них выбирается минимальная величина, которая переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 9.
Содержимое графы 8 равно разности граф 6 и 4 или граф 7 и 5.
| Работа (i,j) | Количество предшествующих работ | Продолжительность tij | Ранние сроки: начало tijР.Н. | Ранние сроки: окончание tijР.О. | Поздние сроки: начало tijП.Н. | Поздние сроки:окончание tijП.О. | Резервы времени: полный tijП | Резервы времени: свободный tijС.В. | Резервы времени: событий Rj |
| (0,1) | 0 | 8 | 0 | 8 | 1 | 9 | 1 | 0 | 1 |
| (0,3) | 0 | 13 | 0 | 13 | 0 | 13 | 0 | 0 | 0 |
| (0,5) | 0 | 9 | 0 | 9 | 11 | 20 | 11 | 11 | 0 |
| (1,2) | 1 | 9 | 8 | 17 | 31 | 40 | 23 | 0 | 23 |
| (1,3) | 1 | 4 | 8 | 12 | 9 | 13 | 1 | 1 | 0 |
| (1,4) | 1 | 6 | 8 | 14 | 20 | 26 | 12 | 9 | 3 |
| (2,7) | 1 | 3 | 17 | 20 | 40 | 43 | 23 | 13 | 10 |
| (3,4) | 2 | 10 | 13 | 23 | 16 | 26 | 3 | 0 | 3 |
| (3,5) | 2 | 7 | 13 | 20 | 13 | 20 | 0 | 0 | 0 |
| (3,6) | 2 | 6 | 13 | 19 | 23 | 29 | 10 | 10 | 0 |
| (4,6) | 2 | 3 | 23 | 26 | 26 | 29 | 3 | 3 | 0 |
| (4,7) | 2 | 8 | 23 | 31 | 35 | 43 | 12 | 2 | 10 |
| (5,6) | 2 | 9 | 20 | 29 | 20 | 29 | 0 | 0 | 0 |
| (5,8) | 2 | 10 | 20 | 30 | 28 | 38 | 8 | 7 | 1 |
| (5,9) | 2 | 6 | 20 | 26 | 36 | 42 | 16 | 16 | 0 |
| (6,7) | 3 | 4 | 29 | 33 | 39 | 43 | 10 | 0 | 10 |
| (6,8) | 3 | 8 | 29 | 37 | 30 | 38 | 1 | 0 | 1 |
| (6,9) | 3 | 13 | 29 | 42 | 29 | 42 | 0 | 0 | 0 |
| (6,10) | 3 | 5 | 29 | 34 | 43 | 48 | 14 | 14 | 0 |
| (7,10) | 3 | 5 | 33 | 38 | 43 | 48 | 10 | 10 | 0 |
| (8,9) | 2 | 4 | 37 | 41 | 38 | 42 | 1 | 1 | 0 |
| (9,10) | 3 | 6 | 42 | 48 | 42 | 48 | 0 | 0 | 0 |
| (9,11) | 3 | 17 | 42 | 59 | 44 | 61 | 2 | 2 | 0 |
| (10,11) | 3 | 13 | 48 | 61 | 48 | 61 | 0 | 0 | 0 |
а) графы 1 и 3 заполняются на основе исходных данных.
б) в графе 2 записывается количество предшествующих работ по сетевому графику или определяется из графы 1 по числу работ, имеющих второй цифрой в коде ту, с которой начинается данная работа.
г) в графе 4 раннее начало работ, выходящих из исходного события, а раннее окончание этих работ равно их продолжительности (гр. 5). Раннее начало последующих работ определяется путем выбора максимального из сроков раннего окончания предшествующих работ. Количество сравниваемых сроков равно количеству предшествующих работ графы 2. Раннее начало последующих работ можно определить после того, как найдено раннее окончание предшествующих. В свою очередь раннее окончание каждой работы находится как сумма величин раннего начала и продолжительности данной работы;
г) продолжительность критического пути определяется после заполнения граф 4 и 5 как максимальная величина из сроков раннего окончания работ, которые ведут к завершающему событию 9;
д) найденная величина критического пути ТKP дням заносится в графу 7 для всех работ, ведущих к завершающему событию. Затем заполнение ведется снизу вверх. Находятся все работы, следующие за рассматриваемой, и определяются разности между поздним окончанием этих работ и их продолжительностями. Минимальная из величин заносится в графу 7;
е) в графе 6 позднее начало работы определяется как разность позднего окончания этих работ и их продолжительности (из значений графы 7 вычитаются данные графы 3);
ж) в графе 8 полный резерв времени работы определяется разностью между значениями граф 7 и 5. Если он равен нулю, то работа является критической;
з) в графе 10 резерв времени событий j определяется как разность позднего окончания работы, заканчивающегося событием j графы 7, и ранним началом работы, начинающимся событием j;
и) значение свободного резерва времени работы определяется как разность значений графы 10 и данных графы 8 и указывает на расположение резервов, необходимых для оптимизации.
Критический путь: (0,3)(3,5)(5,6)(6,9)(9,10)(10,11)
Продолжительность критического пути: 61
Анализ сетевого графика
Сложность сетевого графика оценивается коэффициентом сложности, который определяется по формуле:
Kc = npab / ncob
где Kc – коэффициент сложности сетевого графика; npab – количество работ, ед.; ncob – количество событий, ед.
Сетевые графики, имеющие коэффициент сложности от 1,0 до 1,5, являются простыми, от 1,51 до 2,0 – средней сложности, более 2,1 – сложными.
Kc = 24 / 12 = 2
Поскольку 1.51 < Kc < 2, то сетевой график является средней сложности.
Для оценки вероятности выполнения всего комплекса работ за 60 дней нам необходима следующая формула:
P(tкр
Z - нормативное отклонение случайной величины, Sкр – среднеквадратическое отклонение, вычисляемое как корень квадратный из дисперсии продолжительности критического пути. Соответствие между Z и Ф(Z) представлено в таблице.
Критический путь проходит по работам (0,3)(3,5)(5,6)(6,9)(9,10)(10,11).
Дисперсия критического пути:
S2(Lкр)=S2(0,3) + S2(3,5) + S2(5,6) + S2(6,9) + S2(9,10) + S2(10,11)
S2(Lкр)=0.11 + 1.78 + 2.78 + 0.11 + 0.11 + 1 = 5.89
S(Lкр) = 2.43
p(tкр<60)=0,5+0,5Ф((60-61)/2.43)=0,5+0,5Ф(-0.41)=0,5+0,5*(-0.1591) = 0.3409
Вероятность того, что весь комплекс работ будет выполнен не более чем за 60 дней, составляет 34.09%.
Для определения максимально возможного срока выполнения всего комплекса работ с надежностью 95 % будем использовать следующую формулу:
T=Ткр+Z*Sкр
Для решения поставленной задачи найдем значение аргумента Z, которое соответствует заданной вероятности 95 % (значению графы Ф(Z) 0.95*100% в таблице соответствует Z=1.96).
T=61+1.96*2.43 = 65.76
Максимальный срок выполнения всего комплекса работ при заданном уровне вероятности 95 % составляет всего 65.76 дня.

