Экономические задачи, сводящиеся к транспортной модели

Рассматривается транспортная модель и ее варианты. Такая модель используется для составления наиболее экономичного плана перевозок одного вида продукции из нескольких пунктов (например, заводов) в пункты доставки (например, склады). Транспортную модель можно применять при рассмотрении ряда практических ситуаций, связанных с управлением запасами, составлением сменных графиков, назначением служащих на рабочие места, оборотом наличного капитала, регулированием расхода воды в водохранилищах и многими другими. Кроме того, модель можно видоизменить, с тем чтобы она учитывала перевозку нескольких видов продукции.
Транспортная задача представляет собой задачу линейного программирования, однако ее специфическая структура позволяет так модифицировать симплекс-метод, что вычислительные процедуры становятся более эффективными. При разработке метода решения транспортной задачи существенную роль играет теория двойственности.
В классической транспортной задаче рассматриваются перевозки (прямые или с промежуточными пунктами) одного или нескольких видов продукции из исходных пунктов в пункты назначения. Эту задачу можно видоизменить, включив в нее ограничения сверху на пропускные способности транспортных коммуникаций. Задачу о назначениях и задачу управления запасами можно рассматривать как задачи транспортного типа.

Пример. В пунктах отправления А₁, А₂, А₃ находится однородный груз в количестве a₁, а₂, а₃, соответственно, который необходимо перевезти в пункты назначения В₁, В₂, В₃, потребность каждого из которых составляет b₁, b₂, b₃. Известно расстояние между пунктами перевозок (оценки).
Определить такой план перевозок, при котором общее количество тонно-километров будет минимальной.
Входные данные согласно варианту приведены в таблице 3.

	1	2	3	Запасы
1	10	15	22	50
2	16	20	11	85
3	18	16	33	52
Потребности	62	81	43

Указание: Составить соответствующую задачу математического программирования, привести ее к закрытому типу и решить методом потенциалов.

Математическая модель транспортной задачи:
F=∑∑c_ijx_ij, (1)
при условиях:
∑x_ij = a_i, i = 1,2,…, m, (2)
∑x_ij = b_j, j = 1,2,…, n, (3)
x_ij ≥ 0
Запишем экономико-математическую модель для нашей задачи. Переменные:
x₁₁ – количество груза из 1-го склада в 1-й магазин; x₁₂ – количество груза из 1-го склада в 2-й магазин; x₁₃ – количество груза из 1-го склада в 3-й магазин; x₂₁ – количество груза из 2-го склада в 1-й магазин; x₂₂ – количество груза из 2-го склада в 2-й магазин; x₂₃ – количество груза из 2-го склада в 3-й магазин; x₃₁ – количество груза из 3-го склада в 1-й магазин; x₃₂ – количество груза из 3-го склада в 2-й магазин; x₃₃ – количество груза из 3-го склада в 3-й магазин
Ограничения по запасам:
x₁₁ + x₁₂ + x₁₃ ≤ 50 (для 1 базы)
x₂₁ + x₂₂ + x₂₃ ≤ 85 (для 2 базы)
x₃₁ + x₃₂ + x₃₃ ≤ 52 (для 3 базы)
Ограничения по потребностям:
x₁₁ + x₂₁ + x₃₁ = 62 (для 1 магазина)
x₁₂ + x₂₂ + x₃₂ = 81 (для 2 магазина)
x₁₃ + x₂₃ + x₃₃ = 43 (для 3 магазина)
Целевая функция: 10x₁₁ + 15x₁₂ + 22x₁₃ + 16x₂₁ + 20x₂₂ + 11x₂₃ + 18x₃₁ + 16x₃₂ + 33x₃₃ → min

Определение оптимального плана транспортных задач, имеющих некоторые усложнения в их постановке

При некоторых реальных условиях перевозки груза из определенного пункта A_i в пункт назначения B_j не могут быть осуществлены. Для определения оптимальных планов таких задач предполагают, что стоимость перевозки единицы груза из пункта Ai в пункт B_j является сколь угодно большой величиной М и при этом условии известными методами находят решение транспортной задачи. Такой подход к нахождению решения ТЗ называется запрещением перевозок.
В отдельных ТЗ дополнительным условием является обеспечение перевозки по соответствующим маршрутам определенного количества груза. Пусть, например, из Ai в B_j требуется обязательно перевезти a_ij единиц груза. Тогда в соответствующую клетку таблицы, находящуюся на пересечении строки A_i и столбца B_j, записывают указанное число a_ij и в дальнейшем считают эту клетку свободной со сколь угодно большой стоимостью перевозки М. Для полученной таким образом новой транспортной задачи находят оптимальный план, который определяет оптимальный план исходной задачи.
Иногда требуется найти решение ТЗ, при котором из A_i в B_j должно быть перевезено не менее заданного количества груза a_ij. Для определения оптимального плана такой задачи считают, что запасы Ai и потребности Bj меньше фактических на a_ij единиц. После этого находят оптимальный план новой ТЗ, на основании которого и определяют решение исходной задачи.

Модель без дефицита

В соответствии с терминологией транспортной модели поставщики представлены обычным и сверхурочным производством для различных этапов. Потребители задаются спросом соответствующих этапов. Затраты на «транспортировку» единицы продукции от любого поставщика к любому потребителю представляются суммой соответствующих производственных затрат и затрат на хранение единицы продукции.
Матрица полных затрат для эквивалентной транспортной задачи приведена в следующей таблице:

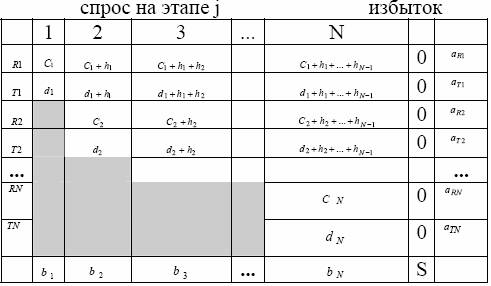
Дополнительный столбец используется для балансировки транспортной задачи, т.е. S = ∑a_i - ∑b_j. Затраты на единицу продукции в дополнительном столбце равны нулю. Так как дефицит не допускается, то продукцию, выпускаемую на рассматриваемом этапе, нельзя использовать для удовлетворения спроса предыдущих этапов. В таблице это ограничение представлено заштрихованными ячейками, что, в сущности, эквивалентно очень большим затратам на единицу продукции.
Так как задолженность в модели не допускается, то для каждого этапа k в нее необходимо включить ограничение, состоящее в том, что накопленный спрос не должен превышать соответствующего общего объема произведенной продукции, т.е. ∑ (a_ri + a_ti) ≥ ∑b_j , k = 1,2,...,N.
Так как спрос на этапе i должен быть удовлетворен прежде, чем спрос на этапах i+1, i+2,..., N, и поскольку на функцию производственных затрат наложены специальные требования, нет необходимости применять общий алгоритм решения транспортной задачи. Сначала путем последовательного назначения максимально возможных поставок по наиболее дешевым элементам первого столбца удовлетворяется спрос на этапе 1. Затем корректируются значения, которые после этого определяют оставшиеся мощности для различных этапов. Далее рассматривается этап 2, и его спрос удовлетворяется наиболее дешевыми поставками в пределах новых ограничений на производственные мощности. Процесс продолжается до тех пор, пока не будет удовлетворен спрос этапа N.

Модель с дефицитом

Рассмотрим обобщение описанной выше модели при условии, что допускается дефицит. Предполагается, что задолженный спрос должен быть удовлетворен к концу N-этапного горизонта планирования. Таблицу 1 можно легко модифицировать, чтобы учесть влияние задолженности, введя соответствующие удельные издержки в заблокированные маршруты.
Так, например, если p_i – удельные потери от дефицита (т.е. на единицу продукции) в случае, когда продукция требуется на этапе i, а поставляется на этапе i+1, то удельные расходы, соответствующие ячейкам R_N,1 и T_R_,1, составляют: {c_N + p1₊p₂ + … + p_N_-1} и {d_N + p1₊p₂ + … + p_N_-1}соответственно.
Заметим, что в общем случае описанный выше алгоритм может не привести к оптимальному решению.