Ранний срок наступления события
Сети или сетевые модели имеют широкое практическое применение. Из всего разнообразия методов и моделей рассмотрим здесь лишь метод критического пути (МКП). Сеть в этом случае – это графическое отображение комплекса работ. Основными элементами сети здесь являются события и работы.Событие – это момент завершения процесса, отображающий отдельный этап выполнения проекта. Комплекс работ начинается с исходного и заканчивается завершающим событием.
Работа – это протяжённый во времени процесс, необходимый для свершения события и, как правило, требующий затрат ресурсов.
События на сетевом графике обычно изображаются кружками, а работы – дугами, соединяющими события. Событие может свершиться только тогда, когда закончатся все работы, ему предшествующие.
В сетевом графике не должно быть "тупиковых" событий, за исключением завершающего, не должно быть событий, которым не предшествует хотя бы одна работа (кроме исходного), не должно быть замкнутых контуров и петель, а также параллельных работ.
Рассмотрение основных понятий и положений МКП будем вести на основе следующего примера. Пусть задана следующая последовательность работ с их временными характеристиками:
| Работа | 1–2 | 1–3 | 1–4 | 2–5 | 3–4 | 3–6 | 4–5 | 4–6 | 4–7 |
| Длительность | 10 | 4 | 6 | 9 | 7 | 8 | 3 | 10 | 4 |
| Работа | 5–8 | 6–7 | 6–9 | 7–8 | 7–10 | 7–9 | 8–10 | 9–10 |
| Длительность | 5 | 9 | 7 | 12 | 8 | 6 | 9 | 11 |
направлены слева направо (рис.2). Над дугами проставлены длительности работ.
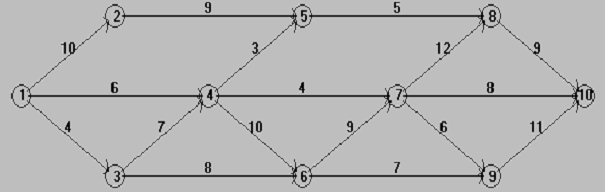
Рис. 2. Сетевой график примера
Критический путь представляет собой путь от начальной до конечной работы, имеющий наибольшую длительность. Любое замедление в выполнении работ критического пути неизбежно приведёт к срыву выполнения всего комплекса работ, поэтому критическому пути и уделяется столько внимания.
Рассмотрим основные понятия, связанные с критическим путём.
Ранний срок наступления события (ЕТ). Он определяется для каждого события при движении по сети слева направо от начального к конечному событию. Для начального события ЕТ = 0. Для других определяется по формуле, где ЕТ1 – ранний срок наступления события i, предшествующего событию j; tij – продолжительность работы (ij).
![]()
Поздний срок наступления события (LТ) – это наиболее поздний срок, в который может наступить событие без задержки выполнения всего комплекса работ. Определяется он при движении по сети справа налево от конечного события к начальному по формуле:
![]()
Для критического пути ранние и поздние сроки наступления событий совпадают. Для конечного события эта величина равна длине критического пути. Расчёт показателей сетевого графика можно производить непосредственно по вышеприведённым формулам. Сначала надо найти ранние сроки наступления событий (при движении по сети слева направо, от начала к концу), (остальное можно выполнить с помощью калькулятора).
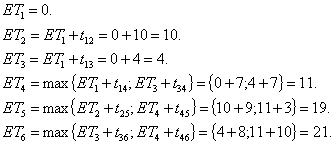
Положить ЕТ10= LT10.
LT7=min{LT8-t78; LT10-t7,10; LT9-t7,9} = {42-12; 51-8; 40-6} = 30; LT9=LT10– t9,10= 51 –11 = 40.
LT8= LT10– t89= 51 – 9 = 42, LT6=min{LT7-t67; LT9-t69}={30-9; 40-7}=21 и т.д.
Возможен и другой способ вычисления показателей – табличный.
События отмечаются в квадратах "главной" диагонали. Работы отмечаются дважды в верхних и нижних "побочных" квадратах относительно главной диагонали таблицы. В верхних "побочных" квадратах таблицы номер строки соответствует предыдущему событию, номер столбца – последующему. В нижних "побочных" квадратах наоборот.
Порядок заполнения таблицы
1. Сначала заполняются числители верхних и нижних побочных квадратов. В них записываются продолжительности соответствующих работ.
2. Заполняются знаменатели верхних "побочных" квадратов как суммы числителя главного квадрата и числителя верхнего "побочного" в той же строке.
3. Числитель первого главного квадрата принимается равным нулю, числители остальных главных квадратов равны максимуму знаменателей верхних "побочных" квадратов в том же столбце.
4. Знаменатель последнего главного квадрата принимается равным числителю этого квадрата. Знаменатели нижних "побочных" квадратов равны разности знаменателя главного и числителя "нижнего" побочного в той же строке.
5. Знаменатели главных квадратов равны минимуму знаменателей "нижних" побочных в том же столбце.
Расчёт показателей сетевого графика
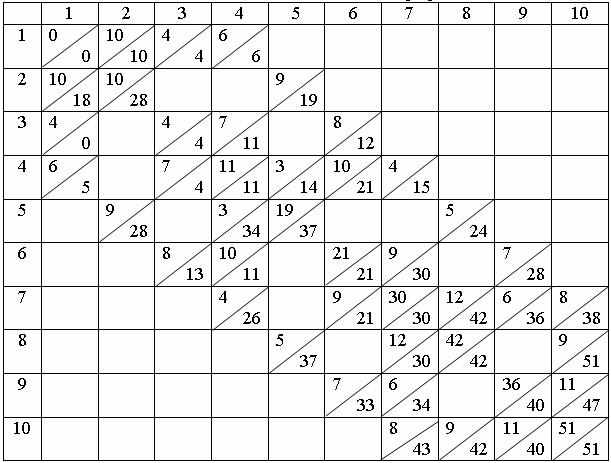
Из таблицы находятся показатели графика:
1. Ранние сроки наступления событий (числители главных квадратов).
2. Поздние сроки наступления событий (знаменатели главных квадратов).
3. Резервы времени событий (разность между знаменателем и числителем главного квадрата). В нашем случае критическими событиями (не имеющими резервов) являются 1, 3, 4, 6, 7, 8, 10. Они составляют критический путь. Продолжительность критического пути равна 51 (числитель или знаменатель последнего главного квадрата).
4. Ранний срок окончания работ (знаменатели верхних "побочных" квадратов).
5. Поздний срок наступления работ (знаменатели соответствующих нижних "побочных" квадратов).
6. Общие резервы времени работ (разность между знаменателем главного квадрата и знаменателем верхнего "побочного" в том же столбце).
7. Свободные резервы времени работ (разность между числителем главного квадрата и знаменателем верхнего "побочного" квадрата в том же столбце).
Воспроизведём график сети, проставив над каждым событием слева – ранний, а справа – поздний сроки наступления события (рис.3).
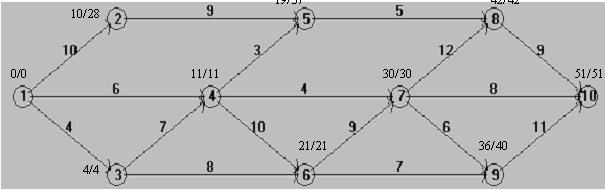
Итак, критический путь проходит вдоль работ 1–3–4–6–7–8–10, и его длительность равна 51.
Резерв времени события определяется как разность между их LT и ET. Ясно, что резервы времени событий вдоль критического пути равны нулю. Для нашего примера резерв времени, например, события 2 равен 28–10 = 18, а события 9 равен 40–36 = 4. На эти промежутки времени может быть задержано выполнение соответствующих работ без риска задержать проект в целом.
Это были временные характеристики событий. Рассмотрим временные характеристики работ. К ним относятся свободный и общий (полный) резервы времени работ.
Общий резерв времени работы (ТS) определяется из соотношения
и показывает, на сколько можно увеличить продолжительность работы при условии, что срок выполнения всего комплекса работ не изменится.
Свободный резерв времени работы (FS) определяется из соотношения
Если свободный резерв времени работ может быть использован по всем работам сети одновременно (тогда все работы становятся критическими), то для полных резервов этого сказать нельзя; его можно использовать или для одной работы пути полностью, или для разных работ частями.
Для критических работ ТS и FS равны нулю. ТS и FS могут быть использованы при выборе календарных сроков выполнения некритических работ и для частичной оптимизации сетевых графиков.
Окончательно имеем:
| критический путь | продолжительность |
1-3 | 4 |
3-4 | 7 |
4-6 | 10 |
6-7 | 9 |
7-8 | 12 |
9-10 | 9 |
общая | 51 |
| Некритические работы | Продолжительность | Общий
резерв TS | Свободный резерв FS |
| 1-2 | 10 | 18 | 0 |
| 1-4 | 6 | 5 | 5 |
| 2-5 | 9 | 18 | 0 |
| 4-5 | 3 | 23 | 5 |
| 3-6 | 8 | 9 | 9 |
| 4-7 | 4 | 15 | 15 |
| 5-8 | 5 | 18 | 18 |
| 6-9 | 7 | 12 | 8 |
| 7-9 | 6 | 4 | 0 |
| 7-10 | 8 | 13 | 13 |
| 9-10 | 11 | 4 | 4 |
Задачи для контрольных заданий №4
По следующим данным построить сеть, аналогичную рассмотренной в примере, определить временные характеристики ее работ и событий, критический путь и его длину. При выполнении данной задачи подставьте вместо n номер своего варианта и полученное число округлить до целого.| Работа | (1,2) | (1,3) | (1,4) | (2,5) | (2,4) | (3,4) | (3,6) | (4,5) | (4,6) |
| Продолжительность | 5+n/3 | 6+n/3 | 7+ n/3 | 4+n | 8+ n/3 | 3+n | 4+n/2 | 10+ n/3 | 2+n |
| (4,7) | (5,7) | (5,8) | (6,7) | (6,9) | (7,8) | (7,9) | (7,10) | (8,10) | (9,10) |
| 8+ n/3 | 9+n/2 | 10+ n/3 | 12+n/2 | 9+n | 7+ n/3 | 5+n | 9+n | 11+n/2 | 8+ n/3 |
