Оптимизация сетевой модели по критерию время – число исполнителей
После построения сетевого графика и определения его временных параметров проводят проверку соответствия полученных сроков продолжительности разработки нормативным или директивным срокам. Далее анализируют структуру сетевой модели, выявляя неоднородность напряженности работ проекта.
В настоящее время на практике сетевую модель вначале корректируют по времени, т. е. приводят ее к заданному сроку окончания проекта. Затем приступают к корректировке графика по критерию распределения ресурсов, начиная с трудовых ресурсов.
Минимизация числа исполнителей проекта при сохранении времени его выполнения
В ходе выполнения комплекса работ занятость работников различной квалификации и разных специальностей оказывается неравномерной. Это приводит к завышению потребности в них с одновременным снижением среднего уровня занятости и, как следствие, к перерасходу заработной платы и увеличению стоимости всего проекта.Наиболее часто на практике приходится оптимизировать сетевой график при ограниченном ресурсе исполнителей определенной категории. Оптимизация по численности исполнителей основана на сдвиге работ в пределах имеющихся у них резервов времени. Ее целью является обеспечение наиболее равномерной занятости работников в течение всего времени выполнения проекта при сохранении общей продолжительности проекта.
Для проведения такой оптимизации часто применяется простой и наглядный графический метод. Согласно сетевой модели составляются линейная диаграмма (график привязки) и карта проекта (график загрузки).
На линейной диаграмме работы отмечают на оси ординат, располагая их снизу вверх по нарастанию индексов. На ось абсцисс наносится равномерная шкала времени (чаще в днях). Каждая работа вычерчивается в масштабе отрезком прямой, длина которой равна продолжительности работы.
Работы критического пути выделяются двойными линиями. Под стрелкой, изображающей работу, помещается в виде висящего флажка численность работников каждой категории, занятых выполнением данной работы. В исходной диаграмме все работы начинаются в свои ранние сроки, а фиктивная работа обозначается точкой.
Проверкой правильности построения линейной диаграммы является срок окончания последней работы проекта, совпадающий с длительностью критического пути. Практическая ценность графика привязки заключается в том, что с его помощью можно улучшать эффективность использования ресурса рабочей силы.
Карта проекта (график загрузки, график ежедневной потребности работников соответствующих категорий) для удобства построения и анализа строится под линейной диаграммой. Для каждого дня определяется суммарное количество исполнителей, занятых на параллельных работах проекта, и откладывается в масштабе по оси ординат. При этом часть исполнителей, занятых на работах критического пути, выделяется пунктиром и штриховкой. Для каждой категории исполнителей строится своя карта проекта. Далее проводится анализ их занятости.
Оптимизация ресурса рабочей силы заключается в одновременном решении двух задач:
- минимизировать количество одновременно занятых исполнителей;
- выровнять потребность в трудовых ресурсах на протяжении всего срока выполнения проекта.
Оптимизация осуществляется перемещением части работ (имеющих резерв времени) с наиболее нагруженных (пиковых) дней на дни, имеющие наименьшую занятость исполнителей. После сдвига работы, работники выполняют ее уже в другие дни, и поэтому для каждого дня изменяется количество исполнителей, занятых одновременно. При оптимизации следует придерживаться следующих рекомендаций:
- перемещение работ по оси времени возможно осуществлять только вправо (откладывая их начало);
- работы критического пути трогать нельзя, т. к. это приведет к увеличению срока выполнения всего проекта;
- работы, имеющие свободный резерв времени, можно спокойно перемещать на величину этого резерва;
- перемещение работ, имеющих только полный резерв времени, требует аналогичного сдвига последующих работ;
- передвигаемые работы на линейной диаграмме выделяют, отмечая заметным символом: звездочкой, штрихом, цветом и т.п.
Различие в использовании свободных и полных резервов заключается в том, что при сдвиге работы с использованием свободного резерва моменты начала последующих за ней работ остаются неизменными (т. е. последующие работы не сдвигаются). При перемещении работы с использованием полного резерва, все последующие работы также сдвигаются.
Оптимизация проводится поэтапно, начиная с участков наибольшей и наименьшей занятости исполнителей. Все линейные диаграммы и карты проекта изображаются аналогично исходным. Число этапов оптимизации зависит от сложности проекта и квалификации корректировщика.
Рассмотрим графический метод на примере оптимизации сетевого графика, представленного табл. 1 и рис.1. Оптимизацию проводим с использованием калькулятора. Его необходимо оптимизировать по числу исполнителей (для простоты в примере принята одна категория исполнителей).
Согласно рекомендациям составим линейную диаграмму и карту проекта (график ежедневной потребности ресурса) и проведем предварительный анализ занятости исполнителей (рис. 2). По графику ежедневной потребности видно, что в разные дни выполнения проекта наблюдается различная занятость исполнителей: сначала их требуется 5 (1-4 дни), затем 15 (5-10 дни), потом только 3 (16-18 дни), снова 8 (20-28 дни), вновь 3 (29-30 дни) и в завершение 6 (31-34 дни). Таким образом, имеем явную неравномерность занятости исполнителей (то перегружены, то недогружены работой).
Таблица 1
| Работа (ij) | Длительность t(ij), дн. | Количество исполнителей |
| 1,2 | 4 | 5 |
| 2,3 | 6 | 3 |
| 2,4 | 5 | 6 |
| 2,7 | 11 | 6 |
| 3,5 | 9 | 1 |
| 4,6 | 9 | 2 |
| 5,7 | 11 | 3 |
| 6,7 | 10 | 5 |
| 7,8 | 4 | 6 |
 Рис. 1. Пример сетевого графика
Рис. 1. Пример сетевого графикаПроведем более детальный анализ линейной диаграммы и карты проекта с целью оптимизации трудовых ресурсов: выравнивая потребность в них на протяжении всего проекта и минимизируя количество одновременно занятых исполнителей. График ежедневной потребности ресурса показывает, что минимальное число исполнителей не может быть меньше 6 человек, что определяется их потребностью для работ критического пути. А 15 исполнителей на участке 5-10 дни проекта является явно завышенным и подлежит коррекции в первую очередь.
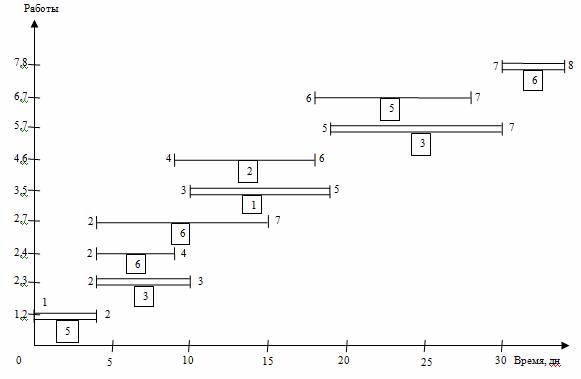
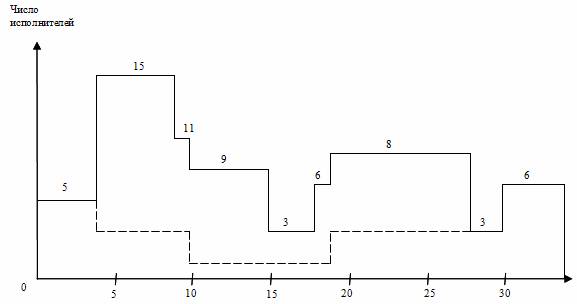
Рис. 2. Линейная диаграмма и карта проекта до оптимизации
15 исполнителей заняты на работах 2,3; 2,4 и 2,7. Работу 2,3 трогать нельзя, т. к. это работа критического пути. Работа 2,4 имеет только полный резерв, но не имеет свободного резерва времени. Работа 2,7 имеет солидный свободный резерв времени и поэтому наиболее предпочтительна для оптимизации. Используем часть свободного резерва, переместив работу 2,7 (5-15 дни) на 5 дней (ее новый срок 10-20 дни). Тем самым максимально необходимое число исполнителей уменьшилось до 9 человек, т.е. задачу минимизации трудовых ресурсов проекта можно принять завершенной.
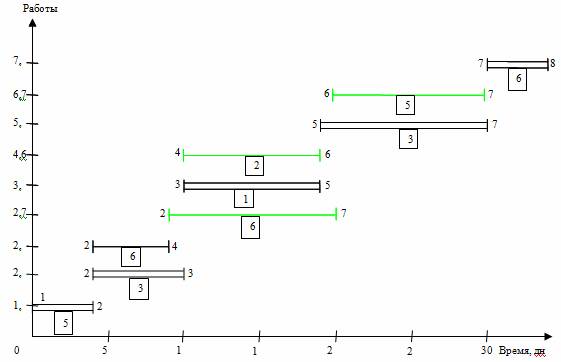
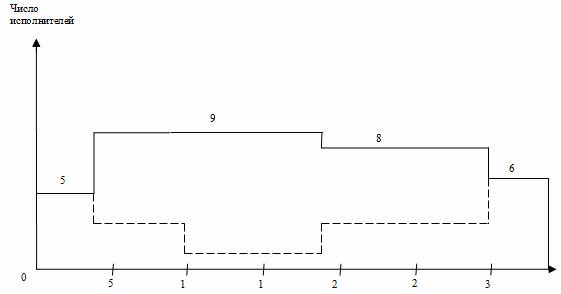
Рис. 3. Линейная диаграмма и карта проекта после оптимизации
Далее решим задачу выравнивания потребности в ресурсах, анализируя интервалы времени, связанные с "провалами" карты проекта. С учетом перемещения работы 2,7 падения спроса на исполнителей в середине проекта (16-18 дни) уже не будет, но он останется ближе к концу проекта (29-30 дни). Чтобы сгладить график загрузки, переместим работу 6,7 (19-28 дни), имеющую свободный резерв времени, на 2 дня (новый срок 21-30 дни). Также для целей выравнивания потребности в трудовых ресурсах переместим работу 4,6 (10-18 дни) на 1 день (11-19 дни).
В итоге оптимизации приходим к линейной диаграмме и карте проекта, представленными на рис. 3. Из графика видно улучшение равномерности загрузки исполнителей: новая ежедневная потребность ресурса составляет от 5 до 9 человек в зависимости от этапа выполнения проекта, резких колебаний занятости нет. Длительность выполнения всего проекта при этом осталась неизменной (34 дня), т. е. необходимое условие оптимизации соблюдено.
Стратегия минимального удорожания комплекса работ при сокращении сроков
Стоимость работ при расчете параметров сетевого графика
Решение: все вычисления будем заносить в таблицу.Перечень работ и их продолжительность перенесем во вторую и третью графы. При этом работы следует записывать в графу 2 последовательно: сначала начиная с номера 1, затем с номера 2 и т.д.
Во второй графе поставим число, характеризующее количество непосредственно предшествующих работ (КПР) тому событию, с которого начинается рассматриваемая работа.
Так, для работы (4,6) в графу 1 поставим число 3, т.к. на номер 4 оканчиваются 3 работы: (1,4),(2,4),(3,4).
Далее заполняем графы 4 и 5. Для работ, имеющих цифру 0 в графе 2, в графу 4 также заносятся нули, а их значения в графе 5 получаются в результате суммирования граф 3 и 4.
Для заполнения следующих строк графы 4, т.е. строк начиная с номера 2, просматриваются заполненные строки графы 5, содержащие работы, которые оканчиваются на этот номер, и максимальное значение переносится в графу 4 обрабатываемых строк.
Этот процесс повторяется до тех пор, пока не будет заполнена последняя строка таблицы.
Заполнение графы 4.
Рассмотрим события: (1,2): 4. Заносим значение 4 в графу.
Рассмотрим события: (1,3): 2. Заносим значение 2 в графу.
Рассмотрим события: (1,4): 3;(2,4): 6;(3,4): 4. Максимальное значение: 6. Заносим его в графу.
Рассмотрим события: (3,5): 5. Заносим значение 5 в графу.
Графы 6 и 7 заполняются обратным ходом, т.е. снизу вверх. Для этого просматриваются строки, оканчивающиеся на номер последнего события, и из графы 5 выбирается максимальная величина, которая записывается в графу 7 по всем строчкам, оканчивающимся на номер последнего события (т.к. tр(i)= tп(i)).
Процесс повторяется до тех пор, пока не будут заполнены все строчки по графам 6 и 7.
Заполнение графы 7.
Рассмотрим события:
(2,6): 10
(4,6): 10
(5,6): 9
Максимальное значение: 10. Записываем его в графу 7 по всем строчкам, оканчивающимся на номер последнего события 6.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 5. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 5.
(5,6): 10 - 4 = 6;
Данное значение переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 6.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 4. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 4.
(4,6): 10 - 4 = 6;
Данное значение переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 6.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 4. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 4.
(4,6): 10 - 4 = 6;
Данное значение переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 6.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 4. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 4.
(4,6): 10 - 4 = 6;
Данное значение переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 6.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 3. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 3.
(3,4): 6 - 2 = 4;
(3,5): 6 - 3 = 3;
В графу 6 среди них выбирается минимальная величина, которая переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 3.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 2. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 2.
(2,4): 6 - 2 = 4;
(2,6): 10 - 6 = 4;
В графу 6 среди них выбирается минимальная величина, которая переносится в графу 7 по обрабатываемым строчкам.. В нашем случае это значение: 4.
Содержимое графы 8 равно разности граф 6 и 4 или граф 7 и 5.
| Работа (i,j) | Количество предшествующих работ | Продолжительность tij | Ранние сроки: начало tijР.Н. | Ранние сроки: окончание tijР.О. | Поздние сроки: начало tijП.Н. | Поздние сроки:окончание tijП.О. | Резервы времени: полный tijП | Резервы времени: свободный tijС.В. | Резервы времени: событий Rj |
| (1,2) | 0 | 4 | 0 | 4 | 0 | 4 | 0 | 0 | 0 |
| (1,3) | 0 | 2 | 0 | 2 | 1 | 3 | 1 | 0 | 1 |
| (1,4) | 0 | 3 | 0 | 3 | 3 | 6 | 3 | 3 | 0 |
| (2,4) | 1 | 2 | 4 | 6 | 4 | 6 | 0 | 0 | 0 |
| (2,6) | 1 | 6 | 4 | 10 | 4 | 10 | 0 | 0 | 0 |
| (3,4) | 1 | 2 | 2 | 4 | 4 | 6 | 2 | 2 | 0 |
| (3,5) | 1 | 3 | 2 | 5 | 3 | 6 | 1 | 0 | 1 |
| (4,6) | 3 | 4 | 6 | 10 | 6 | 10 | 0 | 0 | 0 |
| (5,6) | 1 | 4 | 5 | 9 | 6 | 10 | 1 | 1 | 0 |
Критический путь: (1,2)(2,4)(2,6)(4,6)
Продолжительность критического пути: 10
Анализ сетевого графика
Сложность сетевого графика оценивается коэффициентом сложности, который определяется по формуле:
Kc = npab / ncob
где Kc – коэффициент сложности сетевого графика; npab – количество работ, ед.; ncob – количество событий, ед.
Сетевые графики, имеющие коэффициент сложности от 1,0 до 1,5, являются простыми, от 1,51 до 2,0 – средней сложности, более 2,1 – сложными.
Kc = 9 / 6 = 1.5
Поскольку 1.51 < Kc < 2, то сетевой график является средней сложности.
Коэффициентом напряженности КH работы Pi,j называется отношение продолжительности несовпадающих (заключенных между одними и теми же событиями) отрезков пути, одним из которых является путь максимальной продолжительности, проходящий через данную работу, а другим – критический путь:
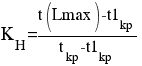
где t(Lmax) – продолжительность максимального пути, проходящего через работу Pi,j, от начала до конца сетевого графика; tkp – продолжительность (длина) критического пути; t1kp – продолжительность отрезка рассматриваемого максимального пути, совпадающего с критическим путем.
Коэффициент напряженности КH работы Pi,j может изменяться в пределах от 0 (для работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности) до 1 (для работ критического пути). Чем ближе к 1 коэффициент напряженности КH работы Pi,j, тем сложнее выполнить данную работу в установленные сроки. Чем ближе Кн работы Pi,j к нулю, тем большим относительным резервом обладает максимальный путь, проходящий через данную работу.
| Работа | Путь | Максимальный путь, t(Lmax) | Совпадающие работы | t1kp | Расчет | КH |
| (1,2) | (1,2)(2,4)(4,6) | 10 | (1,2)(2,4)(4,6) | 10 | (10-10)/(10-10) | 0 |
| (1,3) | (1,3)(3,5)(5,6) | 9 | (1,1) | 0 | (9-0)/(10-0) | 0.9 |
| (1,4) | (1,4)(4,6) | 7 | (4,6) | 4 | (7-4)/(10-4) | 0.5 |
| (2,4) | (1,2)(2,4)(4,6) | 10 | (1,2)(2,4)(4,6) | 10 | (10-10)/(10-10) | 0 |
| (2,6) | (1,2)(2,6) | 10 | (1,2)(2,6) | 10 | (10-10)/(10-10) | 0 |
| (3,4) | (1,3)(3,4)(4,6) | 8 | (4,6) | 4 | (8-4)/(10-4) | 0.67 |
| (3,5) | (1,3)(3,5)(5,6) | 9 | (1,1) | 0 | (9-0)/(10-0) | 0.9 |
| (4,6) | (1,2)(2,4)(4,6) | 10 | (1,2)(2,4)(4,6) | 10 | (10-10)/(10-10) | 0 |
| (5,6) | (1,3)(3,5)(5,6) | 9 | (1,1) | 0 | (9-0)/(10-0) | 0.9 |
Вычисленные коэффициенты напряженности позволяют дополнительно классифицировать работы по зонам. В зависимости от величины Кн выделяют три зоны: критическую (Кн > 0,8); подкритическую (0,6 < Кн < 0,8); резервную (Кн < 0,6).
Далее, что найти стоимость работ, необходимо просуммировать ту стоимость работ, которая приходится на критический путь.
