Транспортная задача линейного программирования. Теория
Под термином "транспортные задачи" понимается широкий круг задач не только транспортного характера. Общим для них является, как правило, распределение ресурсов, находящихся у m производителей (поставщиков), по n потребителям этих ресурсов. На автомобильном транспорте наиболее часто встречаются следующие задачи, относящиеся к транспортным:- прикрепление потребителей ресурса к производителям;
- привязка пунктов отправления к пунктам назначения;
- взаимная привязка грузопотоков прямого и обратного направлений;
- отдельные задачи оптимальной загрузки промышленного оборудования;
- оптимальное распределение объемов выпуска промышленной продукции между заводами-изготовителями и др.
Имеются m пунктов отправления груза А1, А2, ..., Аm и объемы отправления по каждому пункту a1, a2, ..., am. Известна потребность в грузах b1, b2,...,bn по каждому из n пунктов назначения B1, B2,..., Bn. Задана также матрица стоимостей сij, (i = 1,2,...,m, j = 1,2,...,n) доставки груза из пункта i в пункт j. Необходимо рассчитать оптимальный план перевозок, т. е. определить, сколько груза xij должно быть отправлено из каждого пункта отправления (от поставщика) в каждый пункт назначения (до потребителя) с минимальными суммарными транспортными издержками.
На трех складах A1 , A2 и A3 хранится a1 =100, a2=200 и a3 = 60 + 10n единиц одного и того же груза. Этот груз требуется доставить трем потребителям B1, B2 и B3, заказы которых составляют b1 = 190, b2 = 120 и b3 = 10m единиц груза соответственно. Стоимость перевозок cij единицы груза с i-го склада j-му потребителю указаны в правых верхних углах соответствующих клеток транспортной таблицы:
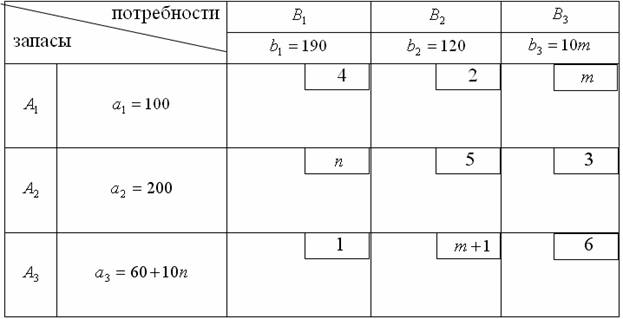
1. Сравнивая суммарный запас
и суммарную потребность 
в грузе, установить, является ли модель транспортной задачи, заданная этой таблицей, открытой или закрытой. Если модель является открытой, то ее необходимо закрыть, добавив фиктивный склад A4’ с запасом a4’=b-a в случае a < b или фиктивного потребителя B4’ с потребностью b4’=a-b в случае a>b и положив соответствующие им тарифы перевозок нулевыми.
2. Составить первоначальный план перевозок. (Рекомендуется воспользоваться методом наименьшей стоимости.)
3. Проверить, является ли первоначальный план оптимальным в смысле суммарной стоимости перевозок, и если это так, то составить оптимальный план
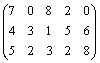
обеспечивающий минимальную стоимость перевозок
. Найти эту стоимость. (Рекомендуется воспользоваться методом потенциалов.)
- Экономические задачи, сводящиеся к транспортной модели
- Постановка транспортной задачи общего вида
- Транспортная задача с промежуточными пунктами
- Транспортная задача в сетевой постановке
- Оптимальное распределение оборудования
- Формирование оптимального штата фирмы
- Задача календарного планирования производства
- Задача о назначениях
- Задача размещения производства
- Оптимальное исследование рынка
- Оптимальное использование рабочих агентов
- Методы составления первоначальных опорных планов
- Опорное решение транспортной задачи
- Транспортная задача линейного программирования
- Двойственная транспортная задача
- Метод ветвей и границ
