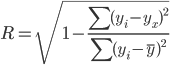Интервальное оценивание параметров распределения
Доверительный интервал и доверительная вероятностьРассчитанная по выборке точечная оценка
параметра θ является приближенным значением θ. Насколько велико отклонение этого приближения от истинного значения? Можно ли доверять этой оценке? Мерой нашего доверия оценке будем считать вероятность γ того, что погрешность оценки |θ-| не превысит заданной точности ε:
(5.1)
Это равенство иначе можно записать так:
т.е. интервал вида 
с заранее заданной вероятностью γ «накрывает» истинное значение параметра θ При этом заранее выбранная вероятность γ называется доверительной вероятностью (или надежностью), а сам интервал — доверительным интервалом (или интервальной оценкой) для параметра θ.
На практике выбирают доверительную вероятность γ из достаточно близких к единице значений
и т.д. Затем по выборочным данным находят точечную оценку и точность оценки ε. После этого определяют границы доверительного интервала .
Поступая таким образом, мы будем ошибаться при многократном проведении испытаний примерно в (1- γ)·100% случаев. Например, если γ =0.997, то ошибочное решение будет приниматься примерно 3 раза на 1000 опытов.
Отметим, что чем уже доверительный интервал для оценки неизвестного параметра, тем лучше. Длина доверительного интервала существенно зависит от объема выборки n (уменьшается с ростом n) и от величины доверительной вероятности γ (увеличивается с приближением γ к единице).