Средняя ошибка доли генеральной совокупности
Доверительный интервал для генеральной доли.где p* - генеральная доля (или вероятность); tkp определяют по таблицам функции Лапласа (при n>30) или таблице распределения Стьюдента (при n≤30).
Пример. Из 12 000 абонентов библиотеки было отобрано случайным образом 200 абонентов для изучения количества прочитанных за год книг. Полученные данные собраны в таблицу:
| Количество книг | 0 – 6 | 6 – 12 | 12 – 18 | 18 – 24 | 24 – 30 | 30 – 36 |
| Количество абонентов | 16 | 35 | 50 | 47 | 32 | 20 |
Задание:
1) Постройте гистограмму распределения абонентов по числу прочитанных книг.
2) Найдите какое среднее количество книг читают абоненты данной библиотеки?
3) Найдите моду и медиану данного ряда распределения. Что означает полученные значения моды и медианы?
4) Может ли данное распределение считаться симметричным? Нормальным? Почему?
5) Найдите выборочную долю каждого представленного в исследовании варианта количества прочитанных книг. И определите примерное число самых активных абонентов библиотеки.
Определите:
1) Дисперсию выборки.
2) Дисперсию доли самых активных абонентов.
3) Среднюю ошибку выборки.
4) Среднюю ошибку для доли самых активных абонентов.
5) В каких пределах (с вероятностью 0,89) может находиться доля самых активных абонентов? В каких пределах в этом случае находится их число?
Решение:
| Группы | x | Кол-во f | x·f | S | (x-x)·f | (x-x)2·f | (x - xср)3* f | (x-x)4·f | Частота (выборочная доля) |
| 0 - 6 | 3 | 16 | 48 | 6 | 241,92 | 3657,83 | -55306,4 | 836232,7 | 0,08 |
| 6 - 12 | 9 | 35 | 315 | 51 | 319,2 | 2911,104 | -26549,2685 | 242129,33 | 0,175 |
| 12 - 18 | 15 | 50 | 750 | 101 | 156 | 486,72 | -1518,5664 | 4737,9272 | 0,25 |
| 18 - 24 | 21 | 47 | 987 | 148 | 135,36 | 389,8368 | 1122,73 | 3233,4624 | 0,235 |
| 24 - 30 | 27 | 32 | 864 | 180 | 284,16 | 2523,3408 | 22407,2663 | 198976,52 | 0,16 |
| 30 - 36 | 33 | 20 | 660 | 200 | 297,6 | 4428,288 | 65892,9254 | 980486,73 | 0,1 |
| 200 | 3624 | 0 | 1434,24 | 14397,12 | 6048,6912 | 2265796,68 | 1 |
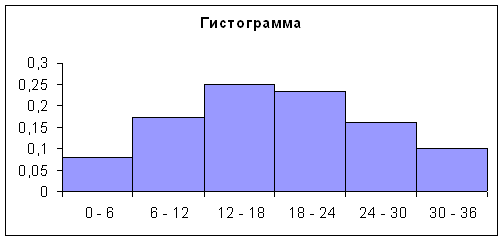
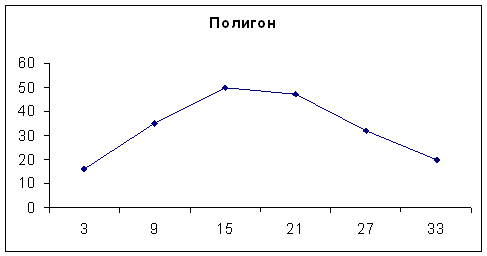
Для оценки ряда распределения найдем следующие показатели:
Показатели центра распределения.
Средняя взвешенная
Мода
Выбираем в качестве начала интервала 12, так как именно на этот интервал приходится наибольшее количество.
Наиболее часто встречающееся значение ряда – 17 абонентов.
Медиана
Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше:
Таким образом, 50% единиц совокупности будут меньше по величине 17.88 абонентов.
Квартили
Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине Q1; 25% будут заключены между Q1 и Q2; 25% - между Q2 и Q3; остальные 25% превосходят Q3
Таким образом, 25% единиц совокупности будут меньше по величине 11.83
Q2 совпадает с медианой, Q2 = 17.88
Остальные 25% превосходят значение 24.38 абонентов.
Квартильный коэффициент дифференциации.
k = Q1 / Q3
k = 11.83 / 24.38 = 0.49
Децили (децентили)
Децили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 10% единиц совокупности будут меньше по величине D1; 80% будут заключены между D1 и D9; остальные 10% превосходят D9.
Таким образом, 10% единиц совокупности будут меньше по величине 6.69
Остальные 10% превосходят 30
Показатели вариации.
Размах вариации
R = Xmax - Xmin
R = 36 - 0 = 36
Среднее линейное отклонение
Каждое значение ряда отличается от другого не более, чем на 7.17 абонентов.
Дисперсия
Несмещенная оценка дисперсии.
Среднее квадратическое отклонение
Каждое значение ряда отличается от среднего значения 18.12 не более, чем на 8.48 абонентов
Оценка среднеквадратического отклонения.
Коэффициент вариации
Поскольку v>30% ,но v<70%, то вариация умеренная
Показатели формы распределения.
Коэффициент осцилляции
Относительное линейное отклонение
Относительный показатель квартильной вариации
Степень асимметрии
Симметричным является распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой
Положительная величина указывает на наличие правосторонней асимметрии
Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения.
Ex > 0 - островершинное распределение
Интервальное оценивание центра генеральной совокупности.
Доверительный интервал для генерального среднего
Поскольку n>30, то определяем значение tkp по таблицам функции Лапласа
В этом случае 2Ф( tkp) = 1 - γ
Ф(tkp) = (1 - γ)/2 = 0.89/2 = 0.445
По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0.445
tkp (γ) = (0.445) = 1.6
(18.12 - 0.95;18.12 + 0.95) = (17.17;19.07)
С вероятностью 0.89 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденном интервала.
Доверительный интервал для дисперсии.
Вероятность выхода за нижнюю границу равна 0.05 / 2 = 0.025. Для количества степеней свободы k = 199, по таблице распределения хи-квадрат находим:
χ2(199) = u
Случайная ошибка дисперсии:
t = (n- 1)*S2 / u
t = 199 • 8.512/u
(72.35 - t; 72.35 + t)
Интервальное оценивание генеральной доли (вероятности события).
Доверительный интервал для генеральной доли.
Поскольку n>30, то определяем значение tkp по таблицам функции Лапласа
В этом случае 2Ф( tkp) = 1 - γ
Ф(tkp) = (1 - γ)/2 = 0.89/2 = 0.445
По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0.445
tkp (γ) = (0.445) = 1.6
| Доля i-ой группы fi/ ∑f | Средняя ошибка выборки для генеральной доли, ε | Нижняя граница доли, p*+ ε | Верхняя граница доли, p*+ ε |
| 0.08 |
| 0.061 |
0.099 |
| 0.175 | | 0.1484 | 0.2016 |
| 0.25 |
| 0.2196 |
0.2804 |
| 0.235 | | 0.2053 | 0.2647 |
| 0.16 |
| 0.1343 |
0.1857 |
| 0.1 | | 0.079 | 0.121 |
Проверка гипотез о виде распределения.
Проверим это предположение с помощью критерия согласия Пирсона
где pi — вероятность попадания в i-й интервал случайной величины, распределенной по гипотетическому закону
Для вычисления вероятностей pi применим формулу и таблицу функции Лапласа
| Интервалы группировки | Наблюдаемая частота ni | Ф(xi) | Ф(xi+1) | Вероятность piпопадания в i-й интервал | Ожидаемая частота npi | Слагаемые статистики Пирсона Ki |
| 0 - 6 | 16 | 0.4236 | 0.4838 | 0.0602 | 12.0400 | 1.3024 |
| 6 - 12 | 35 | 0.2642 | 0.4236 | 0.1594 | 31.8800 | 0.3053 |
| 12 - 18 | 50 | 0.008 | 0.2642 | 0.2562 | 51.2400 | 0.0300 |
| 18 - 24 | 47 | 0.258 | 0.008 | 0.25 | 50.00 | 0.1800 |
| 24 - 30 | 32 | 0.4192 | 0.258 | 0.1612 | 32.2400 | 0.0017 |
| 30 - 36 | 20 | 0.483 | 0.4192 | 0.0638 | 12.7600 | 4.1079 |
| 200 | 5.9273 |
Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).
Её границу Kkp = χ2(k-r-1;a) находим по таблицам распределения χ2 и заданным значениям s, k (число интервалов), r=2 (параметры xcp и s оценены по выборке).
Kkp = 7.8; Kнабл = 5.93
Наблюдаемое значение статистики Пирсона не попадает в критическую область: Кнабл < Kkp, поэтому нет оснований отвергать основную гипотезу. Справедливо предположение о том, что данные выборки имеют нормальное распределение.



