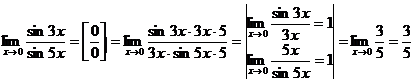Теория пределов. Основные понятия и формулы
Определение 1: Число А называется пределом функции y=f(х) при х, стремящемся к а, если для любого сколь угодно малого положительного числа ε существует такое положительное число δ, что для всех x, удовлетворяющих условию |x-a|≤δ, выполняется неравенство |f(x)-A|≤ε.Предел функции в точке а обозначается
Основные теоремы о пределах
1.
2.
3.
4.
5.
6.
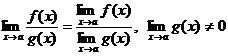
Примечание: Все правила имеют смысл, если пределы функций f(x) и g(x) существуют.
Замечательные пределы
1. Первый замечательный предел 
Следствия из первого замечательного предела 
, 
2. Второй замечательный предел 
Следствие из второго замечательного предела 
Техника вычисления пределов
а) Чтобы раскрыть неопределенность типа
, необходимо числитель и знаменатель дроби разделить на наибольшую степень переменной.
б) Чтобы раскрыть неопределенность типа
, где под знаком предела стоит рациональная дробь, достаточно числить и знаменатель дроби разложить на множители и затем сократить дробь на множитель, приводящий к неопределенности.
в) Чтобы раскрыть неопределенность типа
, если под знаком предела стоит иррациональная дробь, необходимо домножить числитель и знаменатель дроби на сопряженный множитель и сократить множитель приводящий к неопределенности.
г) Необходимо помнить, что
, 
, ∞+C=∞, 
, 
, 
, 0+C=C
Пределы можно вычислить в онлайн режиме.
Пример 1: Вычислить 
Решение: 
Пример 2: Вычислить 
Решение: 
Пример 3: Вычислить 
Решение:
= 
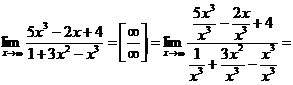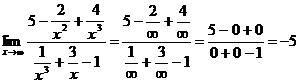
Пример 4: Вычислить 
Решение:
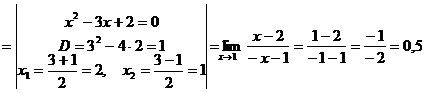
Пример 5: Вычислить 
Решение:
Пример 6: Вычислить 
Решение:
Пример 7: Вычислить 
Решение:
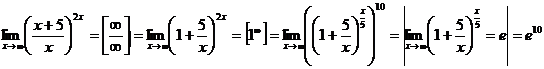
Пример 8: Вычислить 
Решение:
