Сетевое планирование. Теория

1. Параметры сетевых моделей и методы их расчета
2. Расчёт основных показателей сетевого графика
3. Оптимизация сетевой модели по критерию число исполнителей
4. Оптимизация сетевой модели по критерию затраты
5. Оптимизация сетевого графика методом время – стоимость

Работа на графике изображается стрелкой, над которой указывается затрачиваемое на нее время. Длина стрелки и ее ориентация на графике не имеют значения. Желательно только выдерживать направление стрелок так, чтобы начальное событие для работы (обозначается i) располагалось слева в сетевом графике, а конечное (обозначается j) - справа. Для отображения фиктивных работ используют пунктирные стрелки, над которыми время не указывается или проставляется ноль.

Таким образом, событие - это результат выполненной работы, поэтому его формулировка записывается всегда в совершенной форме, не допускающей различного толкования. Например, формулировка работы - "разработка технических условий на печь", формулировка ее конечного события - "технические условия на печь разработаны". Следовательно, событие не имеет продолжительности во времени. Изображается оно кружком или прямоугольником, внутри которого указывается порядковый номер или шифр события.

Правила построения сетевой модели

Правило 2. Ни одна пара операций не должна определяться одинаковыми начальным и конечным событиями. Возможность неоднозначного определения операций через события появляется в случае, когда две или большее число операций допустимо выполнять одновременно.

Правило 3. При включении каждой операции в сетевую модель для обеспечения правильного упорядочения необходимо дать ответы на следующие вопросы:
а) Какие операции необходимо завершить непосредственно перед началом рассматриваемой операции?
б) Какие операции должны непосредственно следовать после завершения данной операции?
в) Какие операции могут выполняться одновременно с рассматриваемой?

При построении сетевого графика следует соблюдать следующие правила:

• в сети не должно быть "тупиков", т.е., событий, от которых не начинается ни одна работа, исключая завершающее событие графика;
• в сети не должно быть событий, не имеющих предшествующего события, кроме исходного события графика;
• в сети не должно быть замкнутых контуров (рис.1);
• в сети не должно быть работ, имеющих одинаковые начальное и конечное события. Для двух работ, выполняемых параллельно, можно ввести дополнительное событие, например i₃ и фиктивную работу (рис. 2).

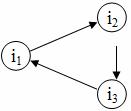Рис. 1. Наличие замкнутых контуров

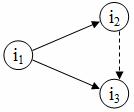Рис. 2. Введение фиктивной работы

Правила построения сетевых графиков

1. В сетевой модели не должно быть «тупиковых» событий, то есть событий, из которых не выходит ни одна работа, за исключением завершающего события.
2. В сетевом графике не должно быть «хвостовых» событий, то есть событий, которым не предшествует хотя бы одна работа, за исключением исходного.
3. В сети не должно быть замкнутых контуров и петель, то есть путей, соединяющих некоторые события с ними же самими.
4. Любые два события должны быть непосредственно связаны не более чем одной работой.
5. В сети рекомендуется иметь одно исходное и одно завершающее событие.
6. Сетевой график должен быть упорядочен. То есть события и работы должны располагаться так, чтобы для любой работы предшествующее ей событие было расположено левее и имело меньший номер по сравнению с завершающим эту работу событием.

• все события сетевого графика подразделяются на ранги,
• к одному рангу может относиться несколько событий,
• нумерация событий производится в соответствии с принадлежностью к тому или иному рангу,
• чем выше ранг, тем больший номер имеет событие,
• внутри одного ранга нумерация событий произвольная.