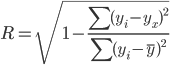Среднее значение по способу моментов
Метод моментов приравнивает моменты теоретического распределения к моментам эмпирического распределения (распределения, построенного по наблюдениям). Из полученных уравнений находятся оценки параметров распределения. Например, для распределения с двумя параметрами первые два момента (среднее и дисперсия распределения, соответственно, m и s) будут приравнены первым двум эмпирическим (выборочным) моментам (среднему и дисперсии выборки, соответственно), и затем будет произведено оценивание.Назначение сервиса. С помощью онлайн-калькулятора вычисляется среднее значение по способу моментов. Результат решения оформляется в формате Word.
Алгоритм нахождения средней по способу моментов
- Определяем параметр A. Вычисляем x*i
- Вычисляем x*i*fi
- Находим среднее значение по формуле
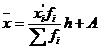
Пример. Затраты рабочего времени на однородную технологическую операцию распределялись между рабочими следующим образом:
| Затраты времени, мин. | Число рабочих, чел. |
| до 15 | 20 |
| 15-20 | 25 |
| 20-25 | 50 |
| 25-30 | 30 |
| 30-35 | 15 |
| более 35 | 10 |
Таблица для расчета показателей.
| Группы | Середина интервала, xi | Кол-во, fi | xi·fi | Накопленная частота, S | (x-x)2·f |
| 5 - 10 | 7.5 | 20 | 150 | 20 | 4600.56 |
| 15 - 20 | 17.5 | 25 | 437.5 | 45 | 667.36 |
| 20 - 25 | 22.5 | 50 | 1125 | 95 | 1.39 |
| 25 - 30 | 27.5 | 30 | 825 | 125 | 700.83 |
| 30 - 35 | 32.5 | 15 | 487.5 | 140 | 1450.42 |
| 35 - 40 | 37.5 | 10 | 375 | 150 | 2200.28 |
| 150 | 3400 | 9620.83 |
Мода
где x0 – начало модального интервала; h – величина интервала; f2 –частота, соответствующая модальному интервалу; f1 – предмодальная частота; f3 – послемодальная частота.
Выбираем в качестве начала интервала 20, так как именно на этот интервал приходится наибольшее количество.
Наиболее часто встречающееся значение ряда – 22.78 мин.
Медиана
Медианным является интервал 20 - 25, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот).
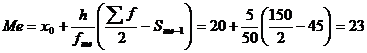
Таким образом, 50% единиц совокупности будут меньше по величине 23 мин.
Среднее значение изучаемого признака по способу моментов.
где А – условный нуль, равный варианте с максимальной частотой (середина интервала с максимальной частотой), h – шаг интервала.
Находим А = 22.5, шаг интервала h = 5.
Средний квадрат отклонений по способу моментов.
| xц | x*i | x*ifi | [x*i]2fi |
| 7.5 | -3 | -60 | 180 |
| 17.5 | -1 | -25 | 25 |
| 22.5 | 0 | 0 | 0 |
| 27.5 | 1 | 30 | 30 |
| 32.5 | 2 | 30 | 60 |
| 37.5 | 3 | 30 | 90 |
| 5 | 385 |
Среднее квадратическое отклонение.
Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.
Поскольку v>30% ,но v<70%, то вариация умеренная.
Пример
| Группы | x | Кол-во f | x·f | (x-x)2·f |
| 6.0 - 8.5 | 7.25 | 26 | 188.5 | 480.74 |
| 8.5 - 11.0 | 9.75 | 112 | 1092 | 362.88 |
| 11.0 - 13.5 | 12.25 | 210 | 2572.5 | 102.9 |
| 13.5 - 16.0 | 14.75 | 52 | 767 | 532.48 |
| 400 | 4620 | 1479 |
Средняя взвешенная
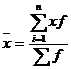
![]()
Среднее значение изучаемого признака по способу моментов.
![]()
где А – условный нуль, равный варианте с максимальной частотой (середина интервала с максимальной частотой), h – шаг интервала.
![]()
Находим А = 12.25.
Шаг интервала h = 2.5.
Средний квадрат отклонений по способу моментов.
![]()
| xц | x*i | x*ifi | [x*i]2fi |
| 7.25 | -2 | -52 | 104 |
| 9.75 | -1 | -112 | 112 |
| 12.25 | 0 | 0 | 0 |
| 14.75 | 1 | 52 | 52 |
| -112 | 268 |
![]()
![]()
Среднеквадратическое отклонение по способу моментов.
![]()
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).
Формула для средневзвешенного:
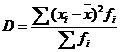
![]()
Среднеквадратическое отклонение.
![]()
Каждое значение ряда отличается от среднего значения 11.55 не более, чем на 1.92.
Как видим, оценки для среднего значения m и квадрата отклонений s рассчитанные по разным формулам совпадают.