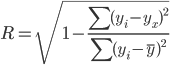Вариация альтернативного признака. Энтропия распределения
Среди множества варьирующих признаков существуют признаки, которыми обладают одни единицы совокупности и не обладают другие. Эти признаки называются альтернативными. Например, ученая степень у преподавателя вуза. Вариация альтернативного признака качественно проявляется в значении нуля у единиц, которые этим признаком не обладают или в значении единицы у тех, которые данный признак имеют.Пусть n – число единиц совокупности; m – число единиц совокупности, обладающих данным признаком; p – доля единиц, обладающих данным признаком (p=m/n); q - доля единиц, не обладающих данным признаком, причем p+q =1.
Альтернативный признак принимает всего два значения – 0 и 1 с весами соответственно q и p. Вычислим среднее значение альтернативного признака по формуле средней арифметической:
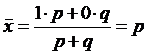 .
.
Дисперсия альтернативного признака определяется по формуле:
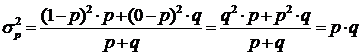
Вычислим дисперсию альтернативного признака по следующим данным: налоговой инспекций одного из районов города проверено 86 коммерческих киосков и в 37 обнаружены финансовые нарушения. Тогда
Следовательно, дисперсия и среднее квадратическое отклонение доли коммерческих киосков, имеющих финансовые нарушения, во всей совокупности обследованных киосков равны:
Показатель энтропии (Hx):
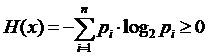 ,
,
где pi – вероятность события xi.
Расчет энтропии распределения можно показать на примере выпуска продукции различных сортов на одном из предприятий точного машиностроения (табл. 5.4).
Таблица 5.4 - Вероятности различных сортов продукции
| Сорт | 1-й | 2-й | 3-й | Брак | Итого |
| Вероятность, pi | 0,90 | 0,04 | 0,05 | 0,01 | 1,00 |
Энтропия данного распределения равна:
H(x)=-(0,9·log20,9+0,04·log20,04 + 0,05·log20,05 + 0,01·log20,01) = 0,6051 бита