Системы эконометрических уравнений
Не всегда получается описать адекватно сложное социально-экономическое явление с помощью только одного соотношения (уравнения). Кроме того, некоторые переменные могут оказывать взаимные воздействия и трудно однозначно определить, какая из них является зависимой, а какая независимой переменной. Поэтому при построении эконометрической модели прибегают к системам уравнений.В любой эконометрической модели в зависимости от конечных прикладных целей ее использования все участвующие в ней переменные подразделяются на:
- Экзогенные (независимые) – значения которых задаются «извне», автономно, в определенной степени они являются управляемыми (планируемыми) (X). Экзогенные переменные модели характеризуются тем, что они являются независимыми и определяются вне системы;
- Эндогенные (зависимые) - значения которых определяются внутри модели, или взаимозависимые (Y).
- Лаговые – экзогенные или эндогенные переменные эконометрической модели, датированные предыдущими моментами времени и находящиеся в уравнении с текущими переменными. Например:
yt – текущая эндогенная переменная,
yt-1 – лаговая эндогенная переменная (отстоящая от текущей на 1 период назад),
yt-2 – тоже лаговая эндогенная переменная (отстоящая от текущей на 2 периода).
Динамические модели экономики содержат в правой части лаговые переменные, а также учитывают тенденцию. - Предопределенные переменные – переменные, определяемые вне модели. К ним относятся лаговые и текущие экзогенные переменные (xt , xt-1), а также лаговые эндогенные переменные (yt-1).
В дальнейшем для простоты будем рассматривать в качестве предопределенных переменных только текущие экзогенные переменные (х).
Пример. Рассмотрим модель зависимости общей величины расходов на питание от располагаемого личного дохода (х) и цены продуктов питания (р):у = а0 + а1х + а2р + ε. Определим класс модели и вид переменных модели: регрессионная модель с одним уравнением; эндогенная переменная — расходы на питание, экзогенные переменные — располагаемый личный доход и цена продуктов питания.
Принципиальные сложности применения систем эконометрических уравнений связаны с ошибками спецификации модели.
Система уравнений в эконометрических исследованиях может быть построена по-разному. Выделяют следующие 3 вида систем уравнений.
- Система независимых уравнений, когда каждая зависимая переменная (y ) рассматривается как функция только от предопределенных переменных (х):

- Система рекурсивных уравнений, когда в каждом последующем уравнении системы зависимая переменная представляет функцию от зависимых и предопределенных переменных предшествующих уравнений:
В рассмотренных 2-ух видах систем каждое уравнение может рассматриваться самостоятельно, и его параметры можно определить с помощью метода наименьших квадратов (МНК).

- Система взаимозависимых (совместных, одновременных) уравнений, когда зависимые переменные в одних уравнениях входят в левую часть (т.е. выступают в роли признаков-результатов), а в других уравнениях – в правую часть системы (т.е. выступают в роли признаков-факторов) одновременно:
В правой части структурной формы взаимозависимой системы могут стоять эндогенные переменные.
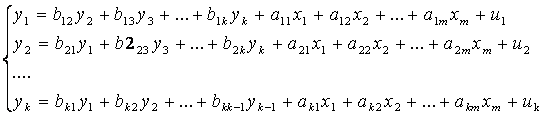
Название «система одновременных уравнений» подчеркивает тот факт, что в системе одни и те же переменные одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других. Система одновременных уравнений отличается от других видов эконометрических систем тем, что в ней одни и те же эндогенные переменные системы в одних уравнениях находятся в левой части, а в других уравнениях — в правой части.
В отличие от предыдущих систем каждое уравнение системы одновременных уравнений не может рассматриваться самостоятельно, и для нахождения его параметров традиционный МНК неприменим, т.к. нарушаются предпосылки, лежащие в основе МНК. В результате оценки параметров получаются смещенными.
В эконометрике эта система уравнений также называется структурной формой модели.
Некоторые из уравнений системы могут быть представлены в виде тождеств, т.е. параметры этих уравнений являются константами.
От структурной формы легко перейти к так называемой приведенной форме модели. Число уравнений в приведенной форме равно числу эндогенных переменных модели. В каждом уравнении приведенной формы эндогенная переменная выражается через все предопределенные переменные модели:

Так как правая часть каждого из уравнений приведенной формы содержит только предопределенные переменные и остатки, а левая часть только одну из эндогенных переменных, то такая система является системой независимых уравнений. Поэтому параметры каждого из уравнений системы в приведенной форме можно определить независимо обычным МНК.
Зная оценки этих приведенных коэффициентов можно определить параметры структурной формы модели. Но не всегда, а только если модель является идентифицируемой.
Проблема идентификации
Модель считается точно идентифицированной, если все ее уравнения точно идентифицированы.Если среди уравнений модели есть хотя бы одно сверхидентифицированное уравнение, то вся модель считается сверхидентифицированной.
Если среди всех уравнений модели есть хотя бы одно неидентифицированное, то вся модель считается неидентифицированной.
Уравнение называется точно идентифицированным, если оценки структурных параметров можно однозначно (единственным способом) найти по коэффициентам приведенной модели.
Уравнение сверхидентифицировано, если для некоторых структурных параметров можно получить более одного численного значения.
Уравнение называется неидентифицированным, если оценки его структурных параметров невозможно найти по коэффициентам приведенной модели.
Количество структурных и приведенных коэффициентов одинаково в модели идентифицируемой.
Правила идентификации
Правила идентификации - необходимое и достаточное условия идентификации (применяются только к структурной форме модели).Введем следующие обозначения:
M - число предопределенных переменных в модели;
m - число предопределенных переменных в данном уравнении;
K – число эндогенных переменных в модели;
k – число эндогенных переменных в данном уравнении.
Необходимое (но недостаточное) условие идентификации уравнения модели:
Для того чтобы уравнение модели было идентифицируемо, необходимо, чтобы число предопределенных переменных, не входящих в уравнение, было не меньше «числа эндогенных переменных, входящих в уравнение минус 1», т.е. : M-m>=k-1;
Если M-m=k-1 , уравнение точно идентифицированно.
Если M-m>k-1, уравнение сверхидентифицированно.
Эти правила следует применять в структурной форме модели.
Достаточное условие идентификации уравнения модели.
Введем обозначения: А – матрица коэффициентов при переменных не входящих в данное уравнение.
Достаточное условие идентификации заключается в том, что ранг матрицы А должен быть равен (К-1). Ранг матрицы – размер наибольшей ее квадратной подматрицы, определитель которой не равен нулю.
Сформулируем необходимое и достаточное условия идентификации уравнения модели:
1) Если M-m>k-1 и ранг матрицы А равен К-1, то уравнение сверхидентифицированно.
2) Если M-m=k-1 и ранг матрицы А равен К-1, то уравнение точно идентифицированно.
3) Если M-m>=k-1 и ранг матрицы А меньше К-1, то уравнение неидентифицированно.
4) Если M-m<k-1, то уравнение неидентифицированно. В этом случае ранг матрицы А будет меньше К-1.
Оценка точно идентифицированного уравнения осуществляется с помощью косвенного метода наименьших квадратов (КМНК).
Алгоритм КМНК включает 3 шага:
1) составление приведенной формы модели и выражение каждого коэффициента приведенной формы через структурные параметры;
2) применение обычного МНК к каждому уравнению приведенной формы и получение численных оценок приведенных параметров;
3) определение оценок параметров структурной формы по оценкам приведенных коэффициентов, используя соотношения, найденные на шаге 1.
Оценка сверхидентифицированного уравнения осуществляется при помощи двухшагового метода наименьших квадратов.
Алгоритм двухшагового МНК
Алгоритм двухшагового МНК включает следующие шаги:1) составление приведенной формы модели;
2) применение обычного МНК к каждому уравнению приведенной формы и получение численных оценок приведенных параметров;
3) определение расчетных значений эндогенных переменных, которые фигурируют в качестве факторов в структурной форме модели;
4) определение структурных параметров каждого уравнения в отдельности обычным МНК, используя в качестве факторов входящие в это уравнение предопределенные переменные и расчетные значения эндогенных переменных, полученные на шаге 1.
Другими словами правильная последовательность шагов алгоритма применения двухшагового МНК включает:
I. Преобразование структурной формы модели в приведенную.
II. Процесс оценки параметров приведенной формы с помощью МНК.
III. Получение по соответствующим приведенным уравнениям теоретических значений эндогенных переменных правой части сверхидентифицируемого уравнения модели.
IV. Процесс оценки параметров сверхидентифицируемого уравнения модели через теоретические значения эндогенных и фактические значения предопределенных переменных;
Рассмотрим пример.
Пусть имеется система:
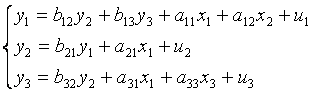
Требуется составить приведенную форму модели, проверить каждое уравнение структурной модели на идентификацию, и предложить способ оценки параметров структурной формы модели.
Решение:
В этой системе y1, y 2,y 3 - эндогенные переменные (K=3);
x1, x 2, x3 - предопределенные переменные ( M=3).
K -1=2; K+M=6.
Составим приведенную форму модели:
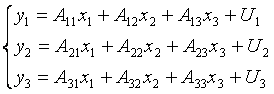
Проверим, как выполняется необходимое условие идентификации для каждого уравнения.
Для 1-ого уравнения имеем: k1=3; m1=2;
M-m1 =1 < k1-1=2, следовательно, 1-ое уравнение неидентифицированно.
Для 2-ого уравнения имеем: k2=2; m2=1;
M-m2 =2 > k2-1=1, следовательно, 2-ое уравнение сверхидентифицированно.
Для 3-его уравнения имеем: k3=2; m3=2;
M-m 3=1 = k3-1=1, следовательно, 3-е уравнение точно идентифицированно.
Рассмотрим, как выполняется достаточное условие идентификации для каждого уравнения системы. Для того, чтобы оно выполнялось необходимо, чтобы определитель матрицы А (матрицы коэффициентов при переменных, не входящих в это уравнение) был равен К-1=2.
Составим матрицу А для 1-ого уравнения системы. В 1-ом уравнении отсутствует лишь одна переменная системы х3. Поэтому матрица А будет иметь вид:
х3
0 - во 2-ом уравнении
a33 - в 3-ем уравнении
Ранг данной матрицы равен 1, что меньше К-1=2, следовательно, 1-ое уравнение модели неидентифицированно.
Составим матрицу А для 2-ого уравнения системы. Во 2-ом уравнении отсутствуют переменные y3, x2, х3:
y3 x 2 x3
b13 a 13 0 - в 1-ом уравнении
1 a32 a33 - в 3-ем уравнении
Ранг данной матрицы равен 2, что равно К-1=2, следовательно, 2-ое уравнение модели точно идентифицированно.
Составим матрицу А для 3-его уравнения системы. В 3-ем уравнении отсутствуют переменные y1, x2:
y 1 x 2
1 a12 - в 1-ом уравнении
b21 0 - во 2-ом уравнении
Ранг данной матрицы равен 1, что меньше К-1=2, следовательно, 3-е уравнение модели неидентифицированно.
Сделаем выводы: 1-ое и 3-е уравнения системы неидентифицированны (т.к. не выполняются достаточные условия идентификации, а в случае 1-ого уравнения и необходимое условие также). 2-ое уравнение системы сверхидентифицированно. Следовательно, система в целом является неидентифицируемой.
Для оценки параметров 2-ого уравнения можно применить двухшаговый МНК. Параметры 1-ого и 3-его уравнений определить по коэффициентам приведенной формы нельзя. Поэтому модель должна быть модифицирована.



