Дерево решений
Пример №1. Требуется принять решение о замене старого оборудования на новое того же вида или его ремонте. Отремонтированное оборудование впоследствии можно частично заменить на новое, более современное, или отремонтировать его заново.Решение определяется будущим спросом на продукцию, которую производят на этом оборудовании.
Полная замена оборудования экономически оправдана при высоком уровне спроса. С другой стороны, можно отремонтировать старое оборудование и через один год, например, заменить его на новое, более совершенное, или заново его отремонтировать.
В данной задаче процесс принятия решения состоит из двух этапов: решение в настоящий момент времени о замене или ремонте оборудования и решение, принимаемое через один год, относительно частичной его замены и ремонта.
Предполагается, что спрос может оказаться высоким, средним и низким.
Дерево решений имеет два типа вершин: "решающие" и "случайные" (рис.).
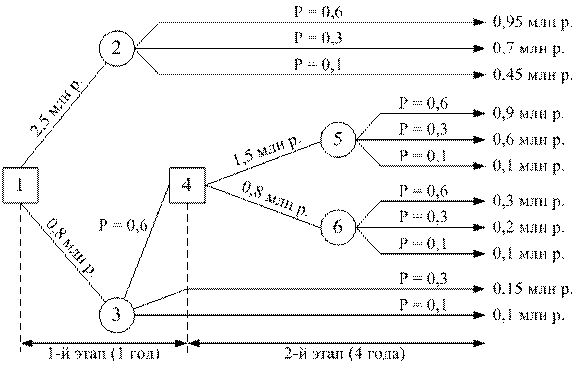
Начиная с "решающей" вершины 1, необходимо принять решение о полной замене оборудования или его ремонте.
Вершины 2 и 3 являются "случайными". Фирма будет рассматривать возможность установления более совершенного оборудования или повторного ремонта старого в том случае, если спрос по истечении одного года установится на высоком уровне. Поэтому в вершине 4 принимается решение о частичной замене старого оборудования более совершенным или ремонте старого. Вершины 5 и 6 "случайные".
Допускается, что фирма рассматривает эту задачу на пятилетний период. Анализ рыночной ситуации показывает, что вероятности высокого, среднего и низкого уровней спроса составляют соответственно 0,6, 0,3 и 0,1. Замена новым оборудованием того же вида, что и старое, обойдется в 2,5 млн р., а ремонт старого – в 0,8 млн р.
Затраты на частичную замену оборудования более совершенным оцениваются в 1,5 млн р., а повторный ремонт старого – в 0,8 млн р.
Ежегодные доходы для каждой стратегии фирмы следующие.
1. Замена старого оборудования на новое того же вида при высоком, среднем и низком уровнях спроса даёт соответственно 0,95, 0,7 и 0,45 млн р.
2. Ремонт старого оборудования при высоком, среднем и низком уровнях спроса оценивается соответственно в 0,3, 0,15 и 0,1 млн р.
3. Частичная замена оборудования на более совершенное при высоком, среднем и низком уровнях спроса составит соответственно 0,9, 0,6 и 0,4 млн р.
4. Повторный ремонт старого оборудования при высоком, среднем и низком уровнях спроса предполагает 0,3, 0,2 и 0,1 млн р. соответственно.
Определим оптимальную стратегию фирмы в замене оборудования.
Решение.
Оценим результаты каждой стратегии и определим, какие решения следует принимать в "решающих" вершинах 1 и 4.
Вычисления начнем с этапа 2. Для последних 4 лет альтернативы, относящиеся к вершине 4, оцениваются так:
ДЧЗ= (0,9 × 0,6 + 0,6 × 0,3 + 0,4 × 0,1) × 4 – 1,5 = 1,54 млн р.,
ДДР = (0,3 × 0,6 + 0,2 × 0,3 + 0,1 × 0,1) × 4 – 0,8 = 0,2 млн р.,
где ДЧЗ– доход от частичной замены оборудования на более совершенное; ДДР– доход от замены оборудования, прошедшего дважды ремонт.
Так как ДЧЗ>ДДР, то в вершине 4 выгоднее частично заменить оборудование на более совершенное, при этом доход составит 1,54 млн р.
Для дальнейших расчетов в вершине 4 можно оставить одну ветвь, которой соответствует доход в 1,54 млн р. за 4 года.
Вычислим доходы на 1-м этапе для "решающей" вершины 1:
ДЗН = (0,95 × 0,6 + 0,7 × 0,3 + 0,45 × 0,1) × 5 – 2,5 = 1,625 млн р.,
ДЗО = 0,3 × 0,6 × 1 + 0,15 × 0,3 × 5 + 0,1 × 0,1 × 5 +1,54 – 0,8 = 1,195 млн р.,
где ДЗН– доход от замены старого оборудования на новое того же вида; ДЗО— доход от отремонтированного оборудования и дальнейшей замены на более совершенное.
Так как ДЗН>ДЗО, то оптимальным решением в вершине 1 является полная замена старого оборудования на новое того же вида.
Итак, оптимальной стратегией фирмы в замене оборудования является полная замена старого оборудования на новое того же вида, при этом доход составит 1,625 млн р.
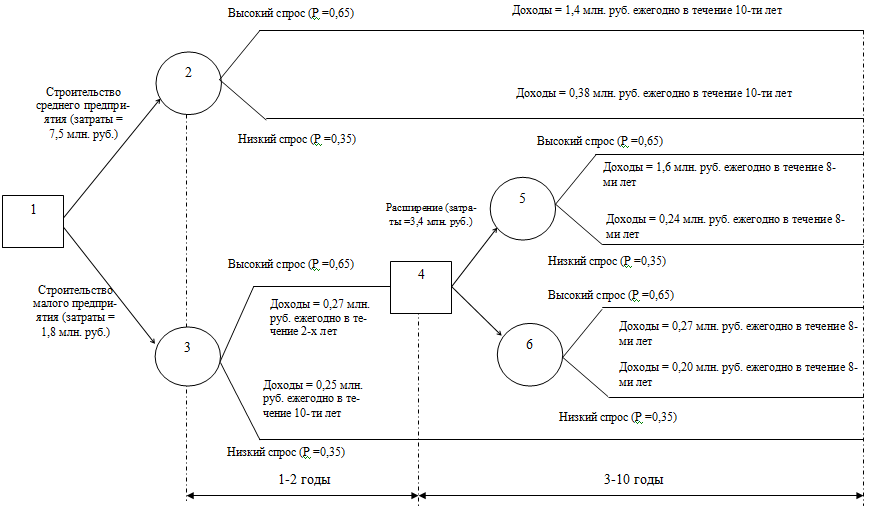
Пример №2. Фирма планирует построить среднее или малое предприятие по производству пользующейся спросом продукции. Решение о строительстве определяется будущим спросом на продукцию, которую предполагается выпускать на планируемом предприятии.
Строительство среднего предприятия экономически оправдано при высоком спросе, но можно построить малое предприятие и через 2 года его расширить.
Фирма рассматривает данную задачу на десятилетний период. Анализ рыночной ситуации, проведенный службой маркетинга, показывает, что вероятности высокого и низкого уровней спроса составляют А=0,65 и В=0,35 соответственно.
Строительство среднего предприятия составит С=7,5 млн. руб., малого – D=1,8 млн. руб. Затраты на расширение малого предприятия оценивается в Е=3,4 млн. руб.
Ожидаемые ежегодные доходы для каждой из возможных альтернатив:
- среднее предприятие при высоком (низком) спросе – F=1,4 (K=0,38) млн. руб.;
- малое предприятие при низком спросе – L=0,25 млн. руб.;
- малое предприятие при высоком спросе – М=0,27 млн. руб.;
- расширенное предприятие при высоком (низком) спросе дает N=1,6 (P=0,24) млн. руб.;
- малое предприятие без расширения при высоком спросе в течение первых двух лет и последующем низком спросе дает R=0,2 млн. руб. за остальные восемь лет.
Решение:
Данная задача является многоэтапной, так как если фирма решит строить малое предприятие, то через два года она может принять решение о его расширении. В этом случае процесс принятия решения состоит из двух этапов: решение в настоящий момент времени о размере предприятия и решение о необходимости его расширения, принимаемое через два года.
На следующем рисунке задача представлена в виде «дерева» решений. Предполагается, что спрос может оказаться высоким и низким. Дерево имеет два типа вершин: «решающие» вершины, обозначенные квадратными узлами, и «случайные» вершины, обозначенные круглыми узлами.
Вычисления начнем со 2-го этапа. Для последних восьми лет альтернативы, относящиеся к вершине 4, оцениваются так:
- доход малого предприятия с последующим расширением:
ДР = (1,6*0,65 + 0,24*0,35)*8 – 3,4 = 5,592 млн. руб.
- доход малого предприятия без расширения
ДБР = (0,27*0,65 + 0,2*0,35)*8 = 1,964 млн. руб.
Таким образом, в вершине 4 выгоднее провести расширение, при этом доход составит 5,592 млн. руб.
Перейдем к вычислениям 1-го этапа. Для вершины 1:
- доход среднего предприятия:
ДС = (1,4*0,65 + 0,38*0,35)*10 – 7,5 = 2,93 млн. руб.
- доход малого предприятия с последующим расширением через 2 года:
ДМ = 5,592 + 0,27*0,65*2 + 0,25*0,35*10 – 1,8 = 5,018 млн. руб.
Сравнивая получаемые в вершине 1 доходы среднего и малого предприятий, видим, что более предпочтительным является вариант строительства малого предприятия с последующим расширением через 2 года.


