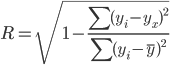Статистические функции в Excel
- Среднее значение:
=СРЗНАЧ(диапазон) - Мода:
=МОДА(диапазон) - Медиана:
=МЕДИАНА(диапазон) - Дисперсия для генеральной совокупности:
=ДИСПР(диапазон) - Среднеквадратическое отклонение:
=СТАНДОТКЛОН(диапазон) - Дисперсия:
=ДИСП(диапазон) - Квадратическое отклонение:
КВАДРОТКЛ(диапазон) - Коэффициент корреляции:
КОРРЕЛ(диапазон 1;диапазон 2) - Прогноз на следующий период:
=ТЕНДЕНЦИЯ(диапазон Y;диапазон X; новое значение Х) - Уравнение регрессии y = bx+a:
=ЛИНЕЙН(диапазон Y;диапазон X;1;1). - Ковариация:
=КОВАР(массив1; массив2).
Пример. В таблице приведены результаты обследования среднемесячной заработной платы (в тыс. руб.) 100 работников одного предприятия (X – среднемесячная заработная плата, k=7, α=0.05).
| 51.5 | 69.6 | 75.6 | 66.5 | 63.4 | 67.5 | 53.3 | 69.7 | 56.5 | 66.5 |
| 61.8 | 72.0 | 76.8 | 70.9 | 66.0 | 67.8 | 58.5 | 83.8 | 62.9 | 76.0 |
| 84.6 | 54.2 | 49.3 | 73.5 | 64.6 | 56.0 | 52.8 | 70.9 | 76.7 | 71.4 |
| 69.4 | 63.8 | 80.6 | 59.1 | 85.4 | 65.0 | 61.5 | 69.2 | 56.5 | 90.4 |
| 75.2 | 87.1 | 70.4 | 65.8 | 63.2 | 79.8 | 74.8 | 62.9 | 84.5 | 78.8 |
| 57.6 | 74.5 | 73.8 | 64.2 | 79.1 | 75.5 | 62.2 | 75.9 | 66.6 | 72.6 |
| 58.3 | 75.3 | 66.4 | 78.2 | 78.3 | 75.0 | 72.0 | 59.9 | 47.4 | 69.4 |
| 61.0 | 76.6 | 78.3 | 69.9 | 69.9 | 76.4 | 91.0 | 53.5 | 69.4 | 65.3 |
| 63.5 | 71.0 | 72.0 | 76.4 | 75.0 | 57.6 | 81.4 | 67.8 | 67.5 | 64.2 |
| 64.7 | 68.2 | 74.9 | 66.6 | 78.9 | 77.7 | 63.3 | 70.6 | 84.3 | 69.9 |
1. Определить выборочные оценки числовых характеристик случайной величины.
Для нахождения выборочных оценок скопируем данные задачи в один столбец таблицы MS Excel. Выделите полученный столбец и на панели инструментов щелкните на кнопку Сортировка и фильтр. В появившемся окошке нажмите сортировку от А до Я. В выделенном столбце значения упорядочатся от наименьшего к наибольшему.
Проанализируем данные с помощью описательной статистики. Для этого на вкладке Данные в группе Анализ щелкните на кнопку Анализ данных. Откроется диалоговое окно Анализ данных.
Выберите инструмент Описательная статистика и щелкните на кнопке Ок. Откроется диалоговое окно Описательная статистика.
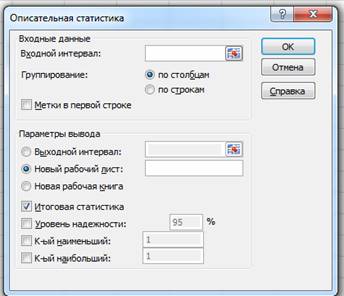
В поле Входной интервал отобразится диапазон $A1:$A100.
Выберите флажок Итоговая статистика. Щелкните на кнопке Ок.
Будет создан новый лист с итоговой статистикой по выбранным данным.
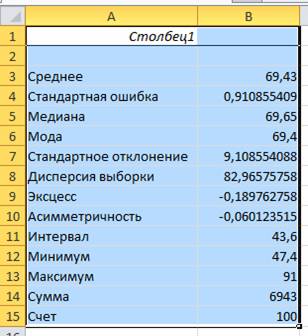
В рассматриваемом случае As=-0,06, Ex=-0,19, что свидетельствует о распределении, близком к нормальному.
2. Построить вариационный ряд, или ряд распределений и гистограмму для него.
Как видно в итоговой статистике, все возможные значения данного распределения укладываются в интервал 3σ.
Действительно, x=69,43; 3σ=27,3; (x-3σ; x+3σ) = (41,13; 96,73)
Размах выборки 43,6. Разбиваем данный ряд на 7 интервалов длины 43,6: 7≈6,2.
Составим таблицу ряда распределений:
Таблица 1.

Чтобы создать диаграмму, выберите нужные данные таблицы (границы интервала и число наблюдений в интервале) и на вкладке Вставка в группе Диаграммы щелкните на типе диаграммы. Появится список доступных подтипов диаграмм. При щелчке на подтипе диаграммы будет создана диаграмма с макетом и цветовой схемой по умолчанию, определенными в теме оформления книги.
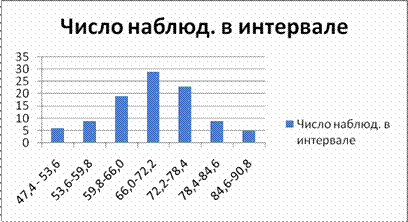
3. Определить теоретическую функцию распределения, её параметры. Выполнить сравнительный графический анализ формы эмпирического и теоретического распределений.
Для построения графика теоретической функции распределения построим вспомогательную таблицу:
Таблица 2.
| Середина интервала | Значение функции Гаусса | Теоретическая вероятность |
| 50,5 | 0,005055791 | 0,003440824 |
| 56,7 | 0,01649618 | 0,011226818 |
| 62,9 | 0,033870577 | 0,023051325 |
| 69,1 | 0,043762967 | 0,029783797 |
| 75,3 | 0,035582452 | 0,024216378 |
| 81,5 | 0,018205807 | 0,012390341 |
| 87,7 | 0,005861772 | 0,003989351 |
Середины интервала скопируем из таблицы 1. Значение функции Гаусса вычислим с помощью встроенной в Excel статистической функции НОРМ.РАСП. Для этого на вкладке Формулы щелкаем на кнопку Другие функции – выбираем Статистические и, среди них находим НОРМ.РАСП. Откроется следующее окно:
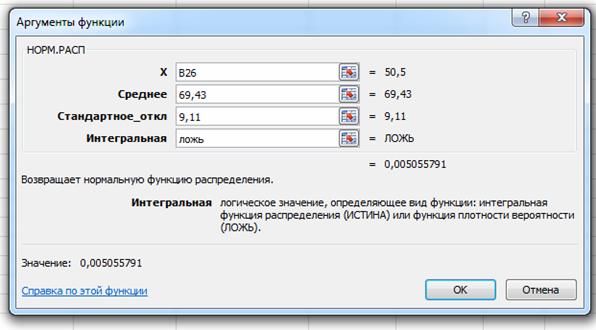
В открывшемся окне в поле X указываем на ячейку со значением середины интервала, в поле Среднее указываем среднее значение, полученное в первом пункте работы с помощью описательной статистики, в поле
Стандартное_откл – стандартное отклонение, найденное также с помощью описательной статистики. В поле Интегральная – ЛОЖЬ, так как ищем функцию плотности вероятности и нажимаем ОК.
Теоретическая вероятность вычисляется по формуле:
В таблице 2 выделяем последний столбец и строим график теоретической вероятности. Для этого на вкладке Вставка в группе График щелкните на типе графика. Появится список доступных подтипов графиков. При щелчке на подтипе графика будет создан график с макетом и цветовой схемой по умолчанию, определенными в теме оформления книги.
Изначально на горизонтальной оси обозначены номера интервалов. Правой кнопкой мыши щелкаем на эту ось и нажимаем на Выбрать данные. Меняем подпись горизонтальной оси, указывая первый столбец таблицы 2. Нажимая на график правой кнопкой мыши можно поменять цвет графика.
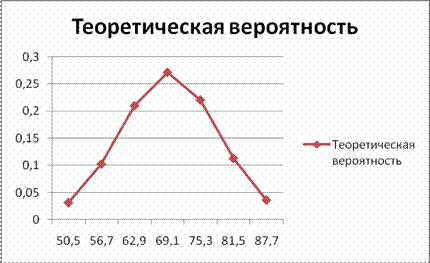
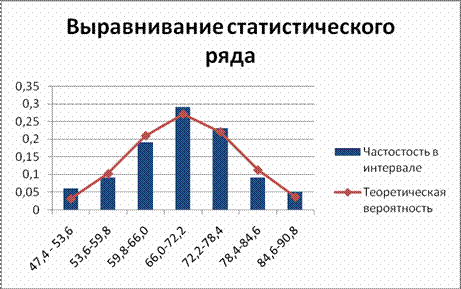
А теперь выполним сравнительный графический анализ формы эмпирического и теоретического распределений построением графика теоретической вероятности на гистограмме частот.
Для этого построим гистограмму частостей на интервалах. Щелкнем правой кнопкой мыши в поле гистограммы и нажмем на кнопку Выбрать данные. В открывшемся окне в левом столбце Элементы легенды нажмем кнопку Добавить. Откроется окно Изменение ряда. Имя ряда: укажем на ячейку Теоретическая вероятность, значения: выделим соответствующую строку. После нажатия Ок появится гистограмма теоретических вероятностей. Укажем на неё правой кнопкой мыши и выберем Изменить тип диаграммы для ряда, выбрав график. Также поменяем цвет нового графика.
4.Проверка согласованности теоретического и эмпирического распределений.
Схема применения критерия Χ2 для проверки гипотезы H0 о соответствии эмпирического ряда нормальному закону распределения, сводится к следующему.
1) Определяется мера расхождения эмпирических и теоретических частот Χ2 по формуле 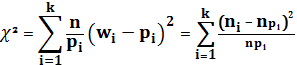 .
.
Для этого в свободной ячейке нажмем на вкладке Формулы выберем Статистические и, среди них ХИ2.ТЕСТ. Откроется следующее окно:
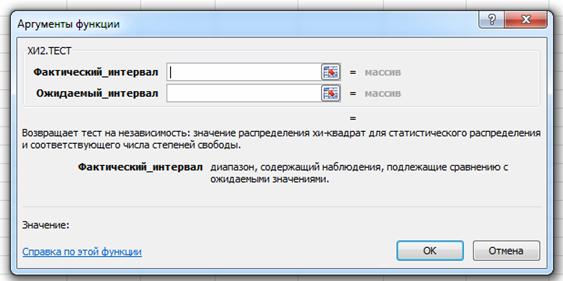
В строке Фактический интервал укажем столбец с частостями из таблицы1. В строке Ожидаемый интервал укажем столбец с теоретическими вероятностями из таблицы2. Нажимая на кнопку Ок, получим наблюдаемое значение Χ2.
2) Для выбранного уровня значимости α находим критическое значение Χ2 при числе свободы k-r-1 (в нашем случае для нормального распределения k-3).
Для этого в свободной ячейке нажмем на вкладке Формулы кнопку Другие функции и выбираем Статистические.Среди них ̶ ХИ2.ОБР.ПХ (так как находим правостороннюю критическую область распределения хи-квадрат). Откроется следующее окно:
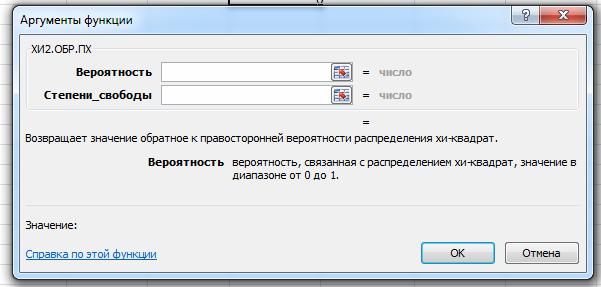
В строку Вероятность введем нужное значение (в нашем случае 0,05), в строку Степенисвободы соответствующее число (в нашем случае 4, так как k=7 – число интервалов разбиения). Нажав на Ок получим критическое значение Χ2.
| Χ2набл | 0,999998579 |
| Χ2критич (при α=0,05, r=7-3=4) | 9,487729037 |
3) Если фактически наблюдаемое значение Χ2 больше критического, то гипотеза H0 отвергается; если наблюдаемое значение не превосходит критического, то гипотеза H0 не противоречит опытным данным.
Так как, Χ2набл<Χ2критич, можно считать, что рассматриваемое распределение подчиняется нормальному закону.