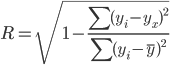Ряды распределения и группировки
Статистический ряд распределения – это упорядоченное распределение единиц совокупности на группы по определённому варьирующему признаку.В зависимости от признака, положенного в основу образования ряда распределения, различают атрибутивные и вариационные ряды распределения.
Наличие общего признака является основой для образования статистической совокупности, которая представляет собой результаты описания или измерения общих признаков объектов исследования.
Предметом изучения в статистике являются изменяющиеся (варьирующие) признаки или статистические признаками.
Виды статистических признаков.
| качественные признаки | количественные признаки | |
| признаки объекта. Они не поддаются непосредственному измерению (например, цвет одежды, национальность, образование и т.п.). | результаты подсчета или измерения. В соответствии с этим они делятся на | |
| дискретные | непрерывные | |
| могут принимать лишь отдельные значения из некоторого ряда чисел. Например, количество человек в семье, число повторений в опыте. | могут принимать любые значения в определенном интервале. Например, температура, скорость движения и т. п. | |
Атрибутивными называют ряды распределения, построенные по качественным признакам. Атрибутивный – это признак, имеющий наименование, (например профессия: швея, учитель и т.д.).
Ряд распределения принято оформлять в виде таблиц. В табл. 2.8 приведён атрибутивный ряд распределения.
Таблица 2.8 - Распределение видов юридической помощи, оказанной адвокатами гражданам одного из регионов РФ.
| N п/п | Виды юридической помощи | Число случаев юридической помощи | |
| всего, тыс. | в % к итогу | ||
| 1 | Устные советы | 5109 | 69,43 |
| 2 | Составление документов | 991 | 13,47 |
| 3 | Поручения по ведению уголовных дел | 1021 | 13,87 |
| 4 | Поручения по ведению Гражданских дел | 238 | 3,23 |
| ВСЕГО | 7359 | 100,00 | |
Вариационными рядами называют ряды распределения, построенные по количественному признаку. Любой вариационный ряд состоит из двух элементов: вариантов и частот.
Вариантами считаются отдельные значения признака, которые он принимает в вариационном ряду.
Частоты – это численности отдельных вариантов или каждой группы вариационного ряда, т.е. это числа, показывающие, как часто встречаются те или иные варианты в ряду распределения. Сумма всех частот определяет численность всей совокупности, её объём.
Частостями называются частоты, выраженные в долях единицы или в процентах к итогу. Соответственно сумма частостей равна 1 или 100 %. Вариационный ряд позволяет по фактическим данным оценить форму закона распределения.
В зависимости от характера вариации признака различают дискретные и интервальные вариационные ряды.
Пример дискретного вариационного ряда приведен в табл. 2.9.
Таблица 2.9 - Распределение семей по числу занимаемых комнат в отдельных квартирах в 1989 г. в РФ.
| N П/п | Группы семей, проживающих в квартирах с числом комнат | Число семей | |
| всего, тыс.ед. | в % к итогу | ||
| 1 | 1 | 4064 | 16,3 |
| 2 | 2 | 12399 | 49,7 |
| 3 | 3 | 7659 | 30,7 |
| 4 | 4 и более | 832 | 3,3 |
| ВСЕГО | 24954 | 100,00 | |
Вариационный ряд
В генеральной совокупности исследуется некоторый количественный признак. Из нее случайным образом извлекается выборка объема n, то есть число элементов выборки равно n. На первом этапе статистической обработки производят ранжирование выборки, т.е. упорядочивание чисел x1, x2, …, xn по возрастанию. Каждое наблюдаемое значение xiназывается вариантой. Частота mi – это число наблюдений значения xi в выборке. Относительная частота (частость) wi– это отношение частоты miк объему выборкиn:
.
При изучении вариационного ряда также используют понятия накопленной частоты и накопленной частости. Пусть x некоторое число. Тогда количество вариантов, значения которых меньше x, называется накопленной частотой: для xi<x.Отношение накопленной частоты к общему числу наблюдений n называется накопленной частостью wimax.
Признак называется дискретно варьируемым, если его отдельные значения (варианты) отличаются друг от друга на некоторую конечную величину (обычно целое число). Вариационный ряд такого признака называется дискретным вариационным рядом.
Таблица 1. Общий вид дискретного вариационного ряда частот
| Значения признака | xi | x1 | x2 | … | xn |
| Частоты | mi | m1 | m2 | … | mn |
Признак называется непрерывно варьирующим, если его значения отличаются друг от друга на сколь угодно малую величину, т.е. признак может принимать любые значения в некотором интервале. Непрерывный вариационный ряд для такого признака называется интервальным.
Таблица 2. Общий вид интервального вариационного ряда частот
| Интервалы | ai – ai+1 | a1 – a2 | a2 – a3 | … | ak – ak+1 |
| Частоты | mi | m1 | m2 | … | mn |
Таблица 3. Графические изображения вариационного ряда
| Ряд | Полигон или гистограмма | Кумулята | Эмпирическая функция распределения |
| Дискретный | 
| 
| 
|
| Интервальный | 
| 
| 
|
Для графического изображения вариационных рядов наиболее часто используются полигон, гистограмма, кумулятивная кривая и эмпирическая функция распределения.
В табл. 2.3 (Группировка населения России по размеру среднедушевого дохода в апреле 1994г.) представлен интервальный вариационный ряд.
Удобно ряды распределения анализировать при помощи графического изображения, позволяющего судить и о форме распределения. Наглядное представление о характере изменения частот вариационного ряда дают полигон и гистограмма.
Полигон используется при изображении дискретных вариационных рядов.
Изобразим, например графически распределение жилого фонда по типу квартир, (табл. 2.10).
Таблица 2.10 - Распределение жилого фонда городского района по типу квартир (цифры условные).
| N п/п | Группы квартир по числу комнат | Число квартир, тыс.ед. |
| 1 | 1 | 10 |
| 2 | 2 | 35 |
| 3 | 3 | 30 |
| 4 | 4 | 15 |
| 5 | 5 | 5 |
| ВСЕГО | 95 | |
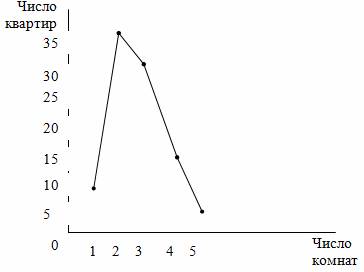
На оси ординат могут наноситься не только значения частот, но и частостей вариационного ряда.
Гистограмма принимается для изображения интервального вариационного ряда. При построении гистограммы на оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенными на соответствующих интервалах. Высота столбиков в случае равных интервалов должна быть пропорциональна частотам. Гистограмма – график, на котором ряд изображен в виде смежных друг с другом столбиков.
Изобразим графически интервальный ряд распределения, приведённый в табл. 2.11.
Таблица 2.11 - Распределение семей по размеру жилой площади, приходящейся на одного человека (цифры условные).
| N п/п | Группы семей по размеру жилой площади, приходящейся на одного человека | Число семей с данным размером жилой площади | Накопленное число семей |
| 1 | 3 – 5 | 10 | 10 |
| 2 | 5 – 7 | 20 | 30 |
| 3 | 7 – 9 | 40 | 70 |
| 4 | 9 – 11 | 30 | 100 |
| 5 | 11 – 13 | 15 | 115 |
| ВСЕГО | 115 | ---- | |
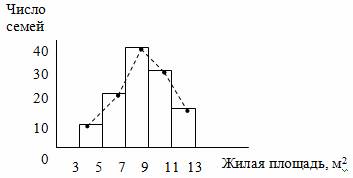
Используя данные накопленного ряда (табл. 2.11), построим кумуляту распределения.
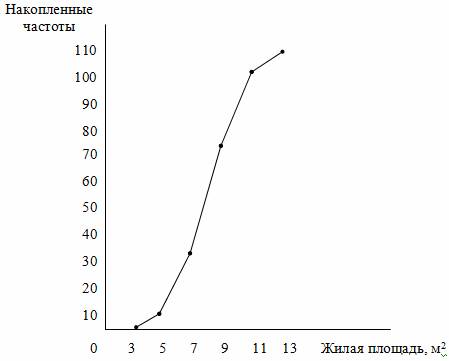Рис. 2.3. Кумулята распределения семей по размеру жилой площади, приходящейся на одного человека
Изображение вариационного ряда в виде кумуляты особенно эффективно для вариационных рядов, частоты которых выражены в долях или процентах к сумме частот ряда.
Если при графическом изображении вариационного ряда в виде кумуляты оси поменять, то мы получим огиву. На рис. 2.4 приведена огива, построенная на основе данных табл. 2.11.
Гистограмма может быть преобразована в полигон распределения, если найти середины сторон прямоугольников и затем эти точки соединить прямыми линиями. Полученный полигон распределения изображён на рис. 2.2 пунктирной линией.
При построении гистограммы распределения вариационного ряда с неравными интервалами по оси ординат наносят не частоты, а плотность распределения признака в соответствующих интервалах.
Плотность распределения – это частота, рассчитанная на единицу ширины интервала, т.е. сколько единиц в каждой группе приходится на единицу величины интервала. Пример расчета плотности распределения представлен в табл. 2.12.
Таблица 2.12 - Распределение предприятий по числу занятых (цифры условные)
| N п/п | Группы предприятий по числу занятых, чел. | Число предприятий | Величина интервала, чел. | Плотность распределения |
| А | 1 | 2 | 3=1/2 | |
| 1 | До 20 | 15 | 20 | 0,75 |
| 2 | 20 – 80 | 27 | 60 | 0,25 |
| 3 | 80 – 150 | 35 | 70 | 0,5 |
| 4 | 150 – 300 | 60 | 150 | 0,4 |
| 5 | 300 – 500 | 10 | 200 | 0,05 |
| ВСЕГО | 147 | ---- | ---- |
Для графического изображения вариационных рядов может также использоваться кумулятивная кривая. При помощи кумуляты (кривой сумм) изображается ряд накопленных частот. Накопленные частоты определяются путём последовательно суммирования частот по группам и показывают, сколько единиц совокупности имеют значения признака не больше, чем рассматриваемое значение.
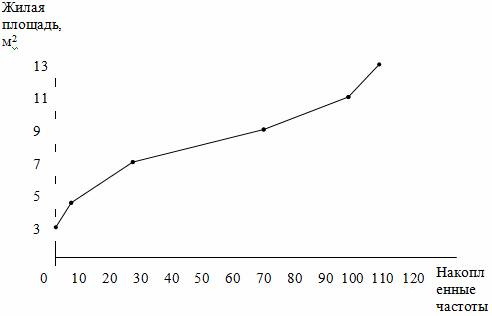
При построении кумуляты интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а по оси ординат накопленные частоты.
Непрерывный вариационный ряд
Непрерывный вариационный ряд - ряд, построенный на основе количественного статистического признака.Пример. Средняя продолжительность заболеваний осужденных (дней на одного человека) в осенне-зимний период в текущем год составила:
| 7,0 | 6,0 | 5,9 | 9,4 | 6,5 | 7,3 | 7,6 | 9,3 | 5,8 | 7,2 |
| 7,1 | 8,3 | 7,5 | 6,8 | 7,1 | 9,2 | 6,1 | 8,5 | 7,4 | 7,8 |
| 10,2 | 9,4 | 8,8 | 8,3 | 7,9 | 9,2 | 8,9 | 9,0 | 8,7 | 8,5 |
Произведите группировку по средней заболеваемости, дней на 1-го человека. Составьте непрерывный вариационный ряд (закрытый и открытый). Укажите, какие из выделяемых групп являются наиболее типичными.
Решение будем проводить с помощью сервиса Группировка данных.
Число групп приближенно определяется по формуле Стэрджесса
n = 1 + 3,2log n
n = 1 + 3,2log(30) = 6
Ширина интервала составит:
h = (Xmax - Xmin)/n
Xmax - максимальное значение группировочного признака в совокупности.
Xmin - минимальное значение группировочного признака.
Определим границы группы.
| Номер группы | Нижняя граница | Верхняя граница |
| 1 | 5.8 | 6.53 |
| 2 | 6.53 | 7.26 |
| 3 | 7.26 | 7.99 |
| 4 | 7.99 | 8.72 |
| 5 | 8.72 | 9.45 |
| 6 | 9.45 | 10.2 |
Одно и тоже значение признака служит верхней и нижней границами двух смежных (предыдущей и последующей) групп.
Для каждого значения ряда подсчитаем, какое количество раз оно попадает в тот или иной интервал. Для этого сортируем ряд по возрастанию.
| 5.8 | 5.8 - 6.53 | 1 |
| 5.9 | 5.8 - 6.53 | 2 |
| 6 | 5.8 - 6.53 | 3 |
| 6.1 | 5.8 - 6.53 | 4 |
| 6.5 | 5.8 - 6.53 | 5 |
| 6.8 | 6.53 - 7.26 | 1 |
| 7 | 6.53 - 7.26 | 2 |
| 7.1 | 6.53 - 7.26 | 3 |
| 7.1 | 6.53 - 7.26 | 4 |
| 7.2 | 6.53 - 7.26 | 5 |
| 7.3 | 7.26 - 7.99 | 1 |
| 7.4 | 7.26 - 7.99 | 2 |
| 7.5 | 7.26 - 7.99 | 3 |
| 7.6 | 7.26 - 7.99 | 4 |
| 7.8 | 7.26 - 7.99 | 5 |
| 7.9 | 7.26 - 7.99 | 6 |
| 8.3 | 7.99 - 8.72 | 1 |
| 8.3 | 7.99 - 8.72 | 2 |
| 8.5 | 7.99 - 8.72 | 3 |
| 8.5 | 7.99 - 8.72 | 4 |
| 8.7 | 7.99 - 8.72 | 5 |
| 8.8 | 8.72 - 9.45 | 1 |
| 8.9 | 8.72 - 9.45 | 2 |
| 9 | 8.72 - 9.45 | 3 |
| 9.2 | 8.72 - 9.45 | 4 |
| 9.2 | 8.72 - 9.45 | 5 |
| 9.3 | 8.72 - 9.45 | 6 |
| 9.4 | 8.72 - 9.45 | 7 |
| 9.4 | 8.72 - 9.45 | 8 |
| 10.2 | 9.45 - 10.18 | 1 |
Результаты группировки оформим в виде таблицы:
| Группы | № совокупности | Частота fi |
| 5.8 - 6.53 | 1,2,3,4,5 | 5 |
| 6.53 - 7.26 | 6,7,8,9,10 | 5 |
| 7.26 - 7.99 | 11,12,13,14,15,16 | 6 |
| 7.99 - 8.72 | 17,18,19,20,21 | 5 |
| 8.72 - 9.45 | 22,23,24,25,26,27,28,29 | 8 |
| 9.45 - 10.18 | 30 | 1 |
Закрытый непрерывный вариационный ряд .
| Группы | Середина интервала, xi | Кол-во, fi |
| 5.8 - 6.53 | 6.17 | 5 |
| 6.53 - 7.26 | 6.9 | 5 |
| 7.26 - 7.99 | 7.63 | 6 |
| 7.99 - 8.72 | 8.36 | 5 |
| 8.72 - 9.45 | 9.09 | 8 |
| 9.45 - 10.18 | 9.82 | 1 |
| 30 |
Открытый непрерывный вариационный ряд
| Группы | Середина интервала, xi | Кол-во, fi |
| до 6.53 | 6.17 | 5 |
| 6.53 - 7.26 | 6.9 | 5 |
| 7.26 - 7.99 | 7.63 | 6 |
| 7.99 - 8.72 | 8.36 | 5 |
| 8.72 - 9.45 | 9.09 | 8 |
| более 9.45 | 9.82 | 1 |
| 30 |
Наиболее типичными из выделяемых групп являются группа [8.72 - 9.45]. Именно на нее приходится наибольшее количество (8). Таким образом, наиболее вероятным является средняя продолжительность заболеваний осужденных (дней на одного человека), которая будет лежать в интервале от 8.72 до 9.45.
При необходимости можно найти характеристики дискретного ряда (показатели распределения) или проверить ряд на вид распределения.
Виды статистических рядов распределения
Дискретный ряд
| X |
| 3,45 |
| 3,89 |
| 5 |
| 3 |
| 2,56 |
| 1,71 |
| 3,34 |
| 4,21 |
Типичное задание для данного вида ряда: сгруппировать ряд, построив равные интервалы. Для полученного ряда найти: среднюю арифметическую, моду, медиану, квартили, децили, дисперсию, среднеквадратическое отклонение, коэффициент вариации. Проверить гипотезу о нормальном распределении полученного ряда.
Интервальный ряд
| группы | число |
| до 20 | 5 |
| 20-25 | 10 |
| 25-30 | 40 |
| 30-35 | 70 |
| 35-40 | 90 |
| 40-45 | 30 |
| 45-50 | 15 |
| свыше 50 | 10 |
| Итого | 270 |
преобразовываем к следующему виду:
| группы | число |
| 15-20 | 5 |
| 20-25 | 10 |
| 25-30 | 40 |
| 30-35 | 70 |
| 35-40 | 90 |
| 40-45 | 30 |
| 45-50 | 15 |
| 50-55 | 10 |
| Итого | 270 |
Типичное задание для данного вида ряда: Для заданного ряда найти: среднюю арифметическую, моду, медиану, квартили, децили, дисперсию, среднеквадратическое отклонение, коэффициент вариации, размах вариации, коэффициент асимметрии, коэффициент осцилляции, линейное отклонение. Проверить гипотезу о нормальном распределении полученного ряда, использую критерий согласия Пирсона.
Вариационный ряд
| Значение | число |
| 20 | 5 |
| 25 | 10 |
| 30 | 40 |
| 35 | 70 |
| 40 | 90 |
| 45 | 30 |
| 50 | 15 |
| 60 | 10 |
| Итого | 270 |
Виды статистических группировок
Статистические группировки делятся на типологические, структурные и аналитические.Типологическая группировка – это разделение исследуемой качественно разнородной совокупности на классы, социально – экономические типы, однородные группы единиц.
Для построения типологической группировки используйте калькулятор (параметр
Дискретный вариационный ряд). Примером типологической группировки является группировка промышленных предприятий по формам собственности (табл. 1).
Таблица 1 - Типологическая группировка промышленных предприятий одного из регионов России по формам собственности в 1994 г.
| № п/п | Группы предприятий по формам собственности | Число предприятий | |
| всего единиц | в % к итогу | ||
| 1 | Федеральная собственность | 26326 | 93,6 |
| 2 | Муниципальная собственность | 89 | 0,3 |
| 3 | Частная собственность | 1366 | 4,9 |
| 4 | Смешанная собственность | 331 | 1,2 |
| ВСЕГО | 28112 | 100,0 | |
Типологические группировки позволяют проследить зарождение, развитие и отмирание различных типов явлений (табл. 2).
Таблица 2 - Группировка предприятий службы сервиса региона России по назначению (1994 г.)
| № п/п | Группы предприятий по назначению | Число приватизированных предприятий (единиц) | |
| 01.04.94г. | 01.07.94г. | ||
| 1 | Розничная торговля (палатки, магазины и др.) | 11194 | 6523 |
| 2 | Общественное питание (столовые, рестораны и др.) | 962 | 2100 |
| 3 | Бытовое обслуживание населения (ателье, мастерские и др.) | 662 | 3871 |
| ВСЕГО | 2818 | 12494 | |
Исследуя табл. 2 отметим, что за 3 месяца число предприятий возросло в 4,4 раза, в том числе предприятий бытового обслуживания населения почти в 6 раз. Наибольшее их количество приходится на розничную торговлю. За исследуемый период численность их возросла на 52 % от общего числа предприятий.
Структурной называется группировка, в которой происходит разделение однородной совокупности на группы, характеризующие ее структуру по какому–либо варьирующему признаку. С помощью таких группировок может изучаться состав населения по полу, возрасту, месту проживания (структурная группировка представлена в табл. 3); состав предприятий по численности занятых, стоимости основных фондов; структура депозитов по сроку их привлечения и т.д.
Для построения структурной группировки используйте калькулятор (параметр Интервальный ряд
).
Таблица 3 - Группировка населения России по размеру среднедушевого дохода в апреле 1994 г.
| № п/п | Группы населения по размеру среднедушевого денежного дохода, тыс. руб. в месяц | Численность населения | |||
| всего, млн. человек | в % к итогу | ||||
| 1 | До 40 | 2,4 | 1,6 | ||
| 2 | 40-80 | 23,4 | 15,8 | ||
| 3 | 80-120 | 34,8 | 23,5 | ||
| 4 | 120-160 | 29,4 | 19,8 | ||
| 5 | 160-200 | 20,7 | 13,9 | ||
| 6 | 200-240 | 13,5 | 9,1 | ||
| 7 | 240-280 | 8,7 | 5,9 | ||
| 8 | 280 и более | 15,5 | 10,4 | ||
| ВСЕГО | 148,4 | 100,0 | |||
Группировка, выявляющая взаимосвязи между изучаемыми явлениями и их признаками, называется аналитической группировкой. Всю совокупность признаков можно разделить на две группы: факторные и результативные. Факторными называются признаки, под воздействием которых меняются, другие результативные, признаки. Взаимосвязь проявляется в том, что с возрастанием значения факторного признака возрастает или убывает среднее значение результативного.
Особенности аналитической группировки следующие:
- в основу группировки кладется факторный признак;
- каждая выделенная группа характеризуется средними значениями результативного признака.
Аналитическая группировка приведена в табл. 4.
Таблица 4 - Группировка коммерческих банков России по сумме активов баланса (данные условные)
| № п/п | Группы банков по сумме активов баланса, млн. руб. | Количество банков, единиц | В среднем на один банк | |||
| численность занятых, человек | балансовая прибыль, млрд. руб. | |||||
| 1 | До 20000 | 19 | 184 | 22,5 | ||
| 2 | 20000-30000 | 8 | 313 | 31,6 | ||
| 3 | 30000-40000 | 7 | 374 | 36,0 | ||
| 4 | 40000-50000 | 9 | 468 | 69,2 | ||
| 5 | 50000 и более | 7 | 516 | 205,6 | ||
| ВСЕГО | 50 | 329 | 60,0 | |||