Геометрическая вероятность

Пример №1. Из промежутка [0; 2] наудачу выбраны два числа x и y. Найдите вероятность того, что эти числа удовлетворяют неравенствам x² ≤ 4y ≤ 4x.
Решение. Испытание состоит в случайном выборе из промежутка [0; 2] пары чисел x и y. Будем это интерпретировать как выбор наудачу точки M(x;y) из множества всех точек квадрата, сторона которого равна двум. Рассмотрим фигуру Ф, представляющую собой множество всех точек квадрата, координаты которых удовлетворяют системе неравенств x² ≤ 4y ≤ 4x. Интересующее событие происходит тогда и только тогда, когда выбранная точка M(x;y) принадлежит фигуре Ф.

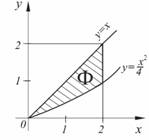
По формуле (8) искомая вероятность равна отношению площади фигуры Ф к площади квадрата:

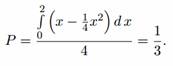
Пример №2. Двое договорились о встрече в определенном месте. Каждый из них приходит в условленное место независимо друг от друга в случайный момент времени из [0;T] и ожидает не более чем время . Какова вероятность встречи на таких условиях?

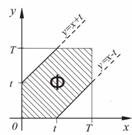
Решение. Обозначим через x время прихода первого в условленное место, а через y — время прихода туда второго лица. Из условия вытекает, что x и y независимо друг от друга пробегают промежуток времени [0;T]. Испытание состоит в фиксации времени прихода указанных лиц к месту встречи. Тогда пространство элементарных исходов данного испытания интерпретируется как совокупность всех точек M(x;y) квадрата Ω={(x;y) : 0 ≤ x ≤ T, 0 ≤ y ≤ T}. Интересующее нас событие A — “встреча произошла” наступает в том и только том случае, когда выбранная точка M(x;y) окажется внутри фигуры Ф, представляющей собой множество всех точек квадрата, координаты которых удовлетворяют неравенству |x – y| ≤ t. По формуле (8) искомая вероятность
представляет собой отношение площади фигуры Ф к площади квадрата Ω:

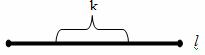
Пример №3. На отрезке l наугад выбраны две точки.
P(0<k<l) - ? , вероятность того, что расстояние между ними меньше k-l

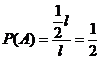
Пример №4. В круг радиуса r случайным образом брошена точка так, что любое ее расположение в круге равновозможно. Найти вероятность того, что она окажется внутри находящегося в круге квадрата со стороной a.
Решение. Вероятность того, что точка окажется внутри лежащего в круге квадрата со стороной а будет равна отношению площади квадрат к площади круга.
Площадь квадрата: Sкв = a².
Площадь круга: S = πr²
Тогда вероятность составит: p = Sкв / S = a² / πr²

см. также Площадь треугольника

Пример №5. С промежутке [0, 4] выбирают наугад два действительных числа. Найдите вероятность того, что их сумма будет больше 4, а произведение - меньше 4.
Решение.
Всего чисел 5: 0,1,2,3,4. Вероятность их появления p=1/5 = 0.2
а) вероятность того, что их сумма будет больше 4
Всего количество таких исходов равно 8:
1+4, 2+3, 2+4, 3+4 и 4+1, 3+2, 4+2, 4+3
P = 0.2*0.2*8 = 0.32
б) произведение - меньше 4.
Всего количество таких исходов равно 13:
0*1, 0*2, 0*3, 0*4, 1*1, 1*2,1*3 и 1*0, 2*0, 3*0, 4*0, 2*1, 3*1
P = 0.2*0.2*13 = 0.52

Задачи для самостоятельного решения
4.3. После бури на участке между 40-м и 70-м километрами телефонной линии произошел обрыв провода. Какова вероятность того, что разрыв произошел между 45-м и 50-м километром линии? (Вероятность обрыва провода в любом месте считать одинаковой).
Ответ: 1/6.

4.4. В круг радиуса r наугад брошена точка. Найдите вероятность того, что эта точка окажется внутри вписанного в данный круг правильного треугольника.
Ответ:

4.5. Найдите вероятность того, что сумма двух случайно выбранных чисел из промежутка [-1; 1] больше нуля, а их произведение отрицательно.
Ответ: 0;25.

4.6. Во время боевой учебы н-ская эскадрилья бомбардировщиков получила задание атаковать нефтебазу “противника”. На территории нефтебазы, имеющей форму прямоугольника со сторонами 30 и 50 м, находятся четыре круглых нефтебака диаметром 10 м каждый. Найдите вероятность прямого поражения нефтебаков бомбой, попавшей на территорию нефтебазы, если попадание бомбы в любую точку этой базы равновероятно.
Ответ: π/15.

4.7. Два действительных числа x и y выбираются наудачу так, что сумма их квадратов меньше 100. Какова вероятность, что сумма квадратов этих чисел окажется больше 64?
Ответ: 0;36.

4.8. Двое друзей условились встретиться между 13 и 14 часами. Пришедший первым ждет второго в течение 20 минут, после чего уходит. Определите вероятность встречи друзей, если моменты их прихода в указанном промежутке времени равновозможны.
Ответ: 5/9.

4.9. Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов равновозможно в течение данных суток. Определите вероятность того, что одному из пароходов придется ожидать освобождения причала, если время стоянки первого парохода равно одному часу, а второго — двум часам.
Ответ: ≈ 0;121.

4.10. Наудачу взяты два положительных числа x и y, каждое из которых не превышает двух. Найдите вероятность того, что произведение x · y будет не больше единицы, а частное y/x не больше двух.
Ответ: ≈ 0;38.

4.11. В области G, ограниченной эллипсоидом , наудачу зафиксирована точка. Какова вероятность того, что координаты (x; y; z) этой точки будут удовлетворять неравенству x²+y²+z²≤4?
Ответ: 1/3.

4.12. В прямоугольник с вершинами R(-2;0), L(-2;9), M (4;9), N (4;0) брошена точка. Найдите вероятность того, что ее координаты будут удовлетворять неравенствам 0 ≤ y ≤ 2x – x²+8.
Ответ: 2/3.

4.13. Область G ограничена окружностью x² + y² = 25, а область g — этой окружностью и параболой 16x - 3y² > 0. Найдите вероятность попадания в область g.
Ответ: ≈ 0;346.

4.14. Наудачу взяты два положительных числа x и y, каждое из которых не превышает единицы. Найдите вероятность того, что сумма x + y не превышает единицы, а произведение x · y не меньше 0,09.
Ответ: ≈ 0;198.