Последовательность независимых опытов
Производятся испытания, в каждом из которых может появиться событие A или событие
. Если вероятность события A в одном испытании не зависит от появления его в любом другом, то испытания называются независимыми относительно события A. Будем считать, что испытания происходят в одинаковых условиях и вероятность появления события A в каждом испытании одна и та же. Обозначим эту вероятность через p, а вероятность появления события через q (q = 1 - p).
Вероятность того, что в серии из n независимых испытаний событие A появится ровно k раз (и не появится n - k раз ), обозначим через Pn(k), тогда
где
Формула называется формулой Бернулли.
Число k0, которому при заданном n соответствует максимальная вероятность Pn(k0), называется наивероятнейшим числом появления события A. При заданных n и p это число определяется неравенствами
- Если число np + p не является целым, то существует одно наивероятнейшее число k0, равное целой части этого числа k0 = [p(n + 1)];
- если np + p – целое число, то k0 имеет два значения:
- если число np – целое, то наивероятнейшее число k0 = np.
Вероятность того, что в n опытах схемы Бернулли событие A появится от k1 до k2 раз (0 ≤ k1 ≤ k2 ≤ n), обозначим через Pn(k1 ≤ k ≤ k2), тогда
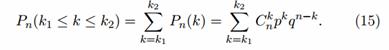
Вероятность Pn(1 ≤ k ≤ n) того, что в n опытах событие A появится хотя бы один раз, определяется формулой
Вероятность того, что в n испытаниях событие A наступит:
а) менее k раз, находят по формуле
б) более k раз:
в) не менее k раз:
г) не более k раз, соответственно
Если
, то удобнее перейти к противоположному событию.
Формулу Бернулли применяют, когда число испытаний n ≤ 10. В случае, когда число испытаний n достаточно велико, на практике пользуются локальной и интегральной теоремами Лапласа.
