Построение уравнения множественной регрессии в Excel
Пакет MS Excel позволяет при построении уравнения линейной регрессии большую часть работы сделать очень быстро. Важно понять, как интерпретировать полученные результаты. Для построения модели регрессии необходимо выбрать пунктСервис/Анализ данных/Регрессия (в Excel 2007 этот режим находится в блоке Данные/Анализ данных/Регрессия). Затем полученные результаты скопировать в блок для анализа.
Регрессия В Excel
Пакет MS Excel позволяет при построении уравнения линейной регрессии большую часть работы сделать очень быстро. Важно понять, как интерпретировать полученные результаты.Для работы необходима надстройка Пакет анализа, которую необходимо включить в пункте меню Сервис/Надстройки.
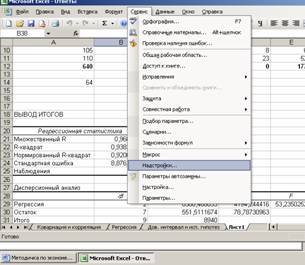
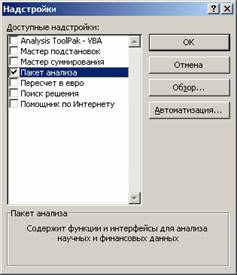

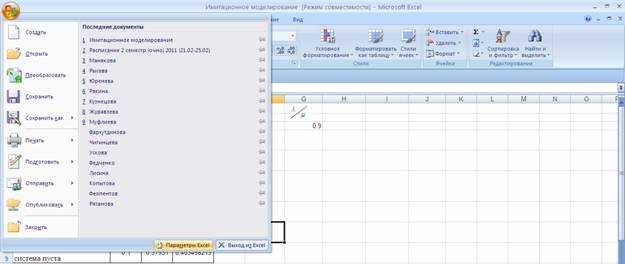
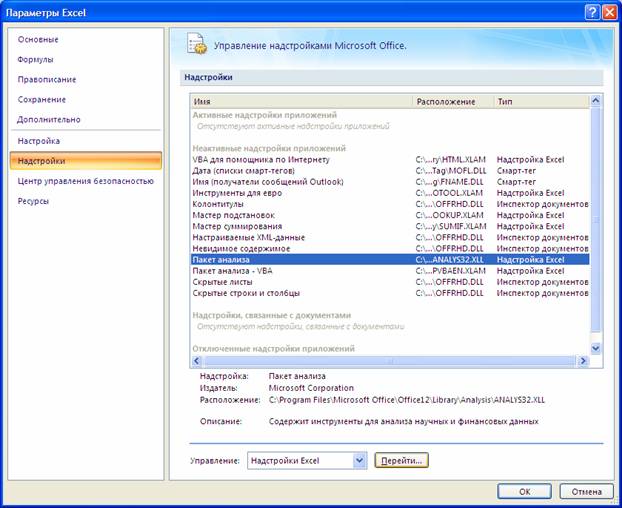
Далее в открывшемся списке нужно выбрать Надстройки, затем установить курсор на пункт Пакет анализа, нажать кнопку Перейти и в следующем окне включить пакет анализа.
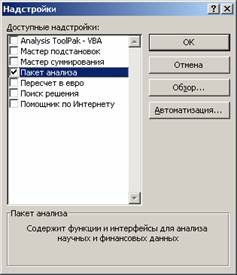
Для построения модели регрессии необходимо выбрать пункт Сервис\Анализ данных\Регрессия. (В Excel 2007 этот режим находится в блоке Данные/Анализ данных/Регрессия) Появится диалоговое окно, которое нужно заполнить:
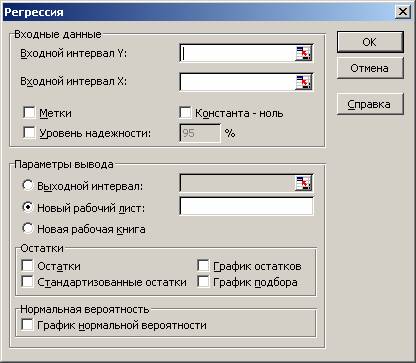
1) Входной интервалY содержит ссылку на ячейки, которые содержат значения результативного признака y. Значения должны быть расположены в столбце;
2) Входной интервалX содержит ссылку на ячейки, которые содержат значения факторов x1, x2, ..,xm (m≤16). Значения должны быть расположены в столбцах;
3) Признак Метки ставится, если первые ячейки содержат пояснительный текст (подписи данных);
4) Уровень надежности - это доверительная вероятность, которая по умолчанию считается равной 95%. Если это значение не устраивает, то нужно включить этот признак и ввести требуемое значение;
5) Признак Константа-ноль включается, если необходимо построить уравнение, в котором свободная переменная a0=0;
6) Параметры вывода определяют, куда должны быть помещены результаты. По умолчанию строит режим Новый рабочий лист;
7) Блок Остатки позволяет включать вывод остатков и построение их графиков.
В результате выводится информация, содержащая все необходимые сведения и сгруппированная в три блока: Регрессионная статистика, Дисперсионный анализ, Вывод остатка. Рассмотрим их подробнее.
1. Регрессионная статистика:
множественный R определяется формулой ![]() ;
;
R-квадрат вычисляется по формуле 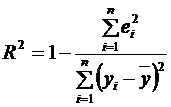 ;
;
Нормированный R-квадрат вычисляется по формуле 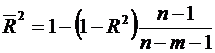 ;
;
Стандартная ошибка S вычисляется по формуле 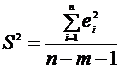 ;
;
Наблюдения - это количество данных n.
2. Дисперсионный анализ, строка Регрессия:
Параметр df равен m (количество наборов факторов x);
Параметр SS определяется формулой  ;
;
Параметр MS определяется формулой ![]() ;
;
Статистика F определяется формулой 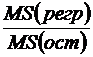 ;
;
Значимость F. Если полученное число превышает α=1-p, то принимается гипотеза R2 = 0 (нет линейной зависимости), иначе принимается гипотеза R2≠0 (есть линейная зависимость).
3. Дисперсионный анализ, строка Остаток:
Параметр df равен n-m-1;
Параметр SS определяется формулой 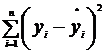 ;
;
Параметр MS определяется формулой ![]() .
.
4. Дисперсионный анализ, строка Итого содержит сумму первых двух столбцов.
5. Дисперсионный анализ, строка Y-пересечение содержит значение коэффициента a0, стандартной ошибки Sb0 и t-статистики tb0.
P-значение - это значение уровней значимости, соответствующее вычисленным t-статистикам. Определяется функцией СТЬЮДРАСП(t-статистика; n-m-1). Если P-значение превышает α=1-p, то соответствующая переменная статистически незначима и ее можно исключить из модели.
Нижние 95% и Верхние 95% - это нижние и верхние границы 95-процентных доверительных интервалов для коэффициентов теоретического уравнения линейной регрессии. Если в блоке ввода данных значение доверительной вероятности было оставлено по умолчанию, то последние два столбца будут дублировать предыдущие. Если пользователь ввел свое значение доверительной вероятности, то последние два столбца содержат значения нижней и верхней границы для указанной доверительной вероятности.
6. Дисперсионный анализ, строки x1, x2,..,xm содержат значения коэффициентов, стандартных ошибок, t-статистик, P-значений и доверительных интервалов для соответствующих xi.
Блок Вывод остатка содержит значения предсказанного y (в наших обозначениях это ![]() ) и остатки
) и остатки ![]() .
.
Алгоритм работы
Вводим заданные значения xi и y, затем выбираем пункт меню Сервис/Анализ данных/Регрессия. Далее указываем интервалы значений xи y, включаем режим Метки, оставляем уровень надежность по умолчанию, указываем выходной интервал и включаем вывод остатков: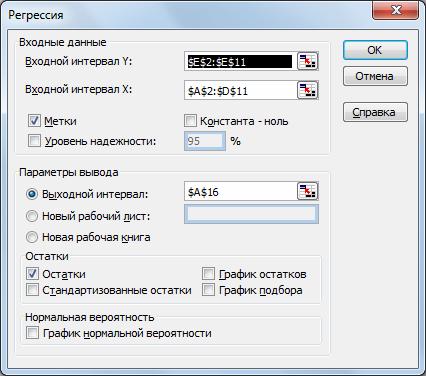
Получаем результат:
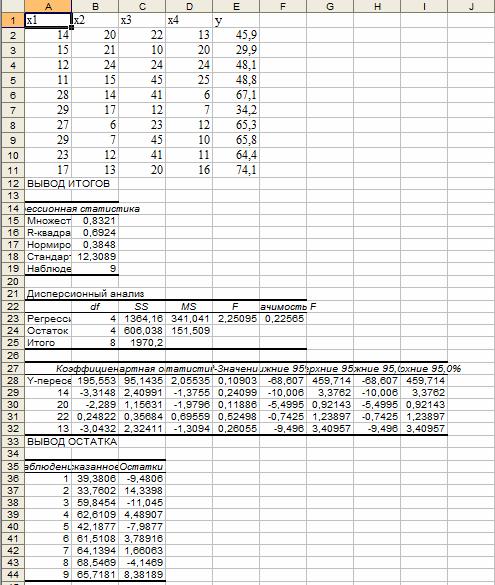
а) Коэффициенты уравнения соответствуют данным столбца Коэффициенты (следующий за столбцомY-пересечения) (блок Дисперсионный анализ).
б) Стандартная ошибка регрессии соответствует значению Стандартная ошибка блока Регрессионная статистика.
Стандартные ошибки коэффициентов соответствуют значениям столбца Стандартная ошибка блока Дисперсионный анализ.
в) Доверительные интервалы соответствуют интервалам Нижние %, Верхние %.
г) Статистическая значимость коэффициентов уравнения соответствует столбцу t-статистика. Граничная точка t(α; n-m-1) вычисляется с помощью функции СТЬЮДРАСПОБР(0,05;n-m-1). Если i-ое значение P-значения меньше a, то i-ый коэффициент статистически значим и влияет на результативный признак.
д) Коэффициент детерминации R-квадрат в блоке Регрессионная статистика. Скорректированный (нормированный) коэффициент детерминации R2n. Это означает, что модель объясняет R2n*100% общего разброса значений результативного признака с учетом поправки на число степеней свободы.
Проверка гипотезы о статистической значимости коэффициента детерминации:
Проводим правостороннюю проверку. Граничная точка Fα;n-m-1 определяется с помощью функции FРАСПОБР(α;m;n-m-1).
Статистика F (определяется из блока Дисперсионный анализ).
Если F> Fα;n-m-1, то гипотеза отвергается H0 и принимает гипотеза H1 на уровне значимости α%.
Этот вывод подтверждает число из столбца Значимость F, которое должно быть меньше значения a.
Статистические таблицы Стьюдента и Фишера
- Среднее значение: СРЗНАЧ(диапазон)
- Квадратическое отклонение: КВАДРОТКЛ(диапазон)
- Дисперсия: ДИСП(диапазон)
- Дисперсия для генеральной совокупности: ДИСПР(диапазон)
- Среднеквадратическое отклонение: СТАНДОТКЛОН(диапазон)
- Уравнение регрессии y = b1x1+b2x2+...bnxn+b0: ЛИНЕЙН(диапазон Y;диапазон X;1;1).
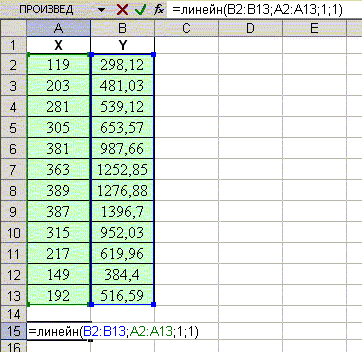
- Выделите блок ячеек размером (n+1) столбцов и 5 строк.
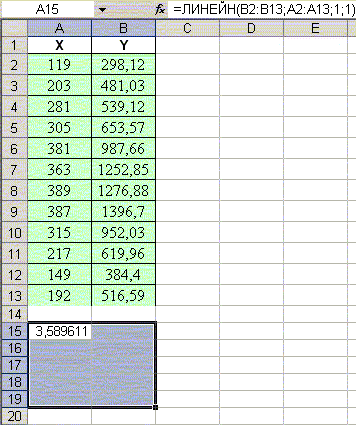
- Перейти в режим редактирования (клавиша F2);
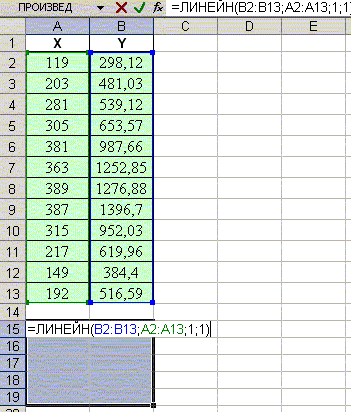
- Нажать клавиши Ctrl+Shift+Enter.
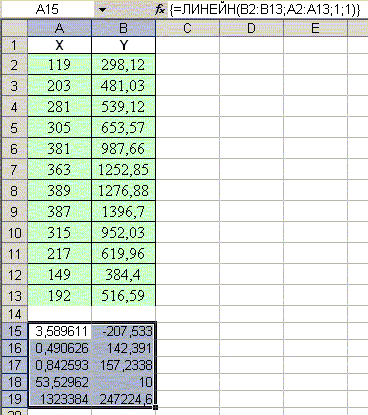
- Выделите блок ячеек размером (n+1) столбцов и 5 строк.
Методические пояснения.
1. Для вычисления коэффициентов регрессии воспользуйтесь встроенной функцией ЛИНЕЙН (функция находится в категории «Статистические»), обратите внимание, что эта функция является функцией массива, поэтому ее использование подразумевает выполнение следующих шагов:
1) В свободном месте рабочего листа выделите область ячеек размером 5 строк и 2 столбца для вывода результатов;
2) В Мастере функций (категория «Статистические») выберите функцию ЛИНЕЙН.
3) Заполните поля аргументов функции:
Известные_значения_y — адреса ячеек, содержащих значения признака ![]() ;
;
Известные_значения_x — адреса ячеек, содержащих значения фактора ![]() ;
;
Константа — значение (логическое), указывающее на наличие свободного члена в уравнении регрессии: укажите в поле Константа значение 1, тогда свободный член рассчитывается обычным образом (если значение поля Константа равно 0, то свободный член полагается равным 0);
Статистика — значение (логическое), которое указывает на то, следует ли выводить дополнительную информацию по регрессионному анализу или нет: укажите в поле Статистика значение равное 1, тогда будет выводиться дополнительная регрессионная информация (если Статистика=0, то выводятся только оценки коэффициентов уравнения регрессии);
4) После того, как будут заполнены все аргументы функции, нажмите комбинацию клавиш <CTRL>+<SHIFT>+<ENTER>.
Результаты расчета параметров регрессионной модели будут выведены в виде следующей таблицы:
Значение коэффициента b | Значение коэффициента a |
Стандартная ошибка mb коэффициента b | Стандартная ошибка ma коэффициента a |
Коэффициент детерминации R2 | Стандартное отклонение остатков Sост |
Значение F-статистики | Число степеней свободы, равное n-2 |
Регрессионная сумма квадратов 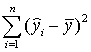
| Остаточная сумма квадратов |
2. Табличные значения распределения Стьюдента определите с помощью функции СТЬЮДРАСПОБР. Аргументы этой функции:
Вероятность — уровень значимости α (можно принять равным 0,05, т.е. 5%);
Степени_свободы — число степеней свободы, для парной линейной регрессии равно n-2, где n — число наблюдений.
3. Табличное значение
Вероятность — уровень значимости α (можно принять равным 0,05, т.е. 5%);
Степени_свободы1 — число степеней свободы числителя, для парной регрессии равно 1 (т.к. один фактор);
Степени_свободы2 — число степеней свободы знаменателя, для парной регрессии равно n-2, где n — число наблюдений.
4. Коэффициент корреляции вычислите с помощью функции КОРРЕЛ. Аргументы функции:
Массив 1ш и Массив 2 — адреса ячеек, в которых содержатся значения величин, для которых вычисляется коэффициент корреляции.
5. Для вычисления (XTX)-1
1) Построите матрицу
 .
.
2) Постройте транспонированную к ней матрицу XT. Для построения матрицы XT необходимо воспользоваться функцией ТРАНСП (категория Ссылки и массивы).
3) матрицу XT необходимо умножить на матрицу X;
Произведение матриц вычисляется с помощью функции МУМНОЖ, аргументами которой являются перемножаемые матрицы. Перемножаемые матрицы должны удовлетворять условию соответствия размеров: матрица размера mxn может быть умножена справа на матрицу размера nxk, в результате получится матрица размера mxk.
В случае множественной регрессии с тремя факторами матрица X будет иметь размер nx4, матрица XT — размер 4xn, а их произведение XTX — размер 4x4.
Функция МУМНОЖ является функцией массива! Поэтому перед использованием функции МУМНОЖ необходимо выделить область размером mxk, в которой будет выведен результат, затем вставить функцию МУМНОЖ, указав ее аргументы. После этого в левой верхней ячейке выделенной области появится первый элемент результирующей матрицы. Для вывода всей матрицы нажмите комбинацию клавиш <CTRL>+<SHIFT>+<ENTER>.
4) найти обратную матрицу (XTX)-1;
Обратную матрицу (XTX)-1 вычислите с помощью функции МОБР. Функция МОБР также является функцией массива и ее использование аналогично функции МУМНОЖ: сначала необходимо выделить область ячеек, в которой будет получена обратная матрица, вставить функцию МОБР, затем <CTRL>+<SHIFT>+<ENTER>.
6. Коэффициенты множественной линейной регрессии вычисляются с помощью функции ЛИНЕЙН. Для того чтобы использовать эту функцию для вычисления параметров множественной регрессии необходимо
1) Сначала выделить на рабочем листе область размером 5x(k+1), где k — число объясняющих переменных.
2) Затем заполнить поля аргументов этой функции, которые имеют тот же смысл, что и в случае парной регрессии:
Известные_значения_y — адреса ячеек, содержащих значения признака y;
Известные_значения_x — адреса ячеек, содержащих значения всех объясняющих переменных.
Обратите внимание: выборочные значения факторов должны располагаться рядом друг с другом (в смежной области), причем предполагается, что в первом столбце (строке) содержатся значения первой объясняющей переменной, во втором столбце — второй и т.д.
Константа — значение (логическое), указывающее на наличие свободного члена в уравнении регрессии: укажите в поле Константа значение 1, тогда свободный член рассчитывается обычным образом (если значение поля Константа равно 0, то свободный член полагается равным 0);
Статистика — значение (логическое), которое указывает на то, следует ли выводить дополнительную информацию по регрессионному анализу или нет: укажите в поле Статистика значение равное 1, тогда будет выводиться дополнительная регрессионная информация (если Статистика=0, то выводятся только оценки коэффициентов уравнения регрессии);
В случае трех объясняющих переменных (k=3) результаты расчета параметров регрессии будут выведены в следующем виде:
| Значение коэффициента b3 | Значение коэффициента b2 | Значение коэффициента b1 | Значение коэффициента a |
| Станд. ошибка mb3коэфф. b3 | Станд. ошибка mb2коэфф. b2 | Станд. ошибка mb1коэфф. b1 | Станд. ошибка maкоэфф. a |
| Коэффициент детерминации R2 | Оценка стандартного отклонения остатков Sост | ||
| Значение F-статистики | Число степеней свободы n-k-1 | ||
Регрессионная сумма квадратов 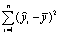 | Остаточная сумма квадратов 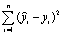 |


