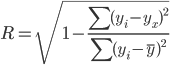Понятие о статистической сводке. Метод группировки
С помощью полученной информации в ходе статистического наблюдения нельзя сделать выводы в целом об объекте без предварительной обработки данных.
Сводка представляет собой комплекс последовательных операций по обобщению конкретных единичных фактов, образующих совокупность, для выявления закономерностей, присущих явлению в целом.
Если при статистическом наблюдении собирают данные о каждой единице объекта, то результатом сводки являются подробные данные, отражающие в целом всю совокупность.
По глубине обработки материала сводка бывает простая и сложная.
Простой сводкой называется операция по подсчету общих итогов по совокупности единиц наблюдения.
Сложная сводка представляет собой комплекс операций, включающих группировку единиц наблюдения, подсчет итогов по каждой группе и по всему объекту и представление результатов группировки и сводки в виде статистических таблиц.
Далее рассмотрим метод группировки.
Определенные единицы статистической совокупности объединяются в группы при помощи метода группировки. Это позволяет «сжать» информацию, полученную в ходе наблюдения, и на этой основе выявить закономерности, присущие изучаемому явлению.
Группировкой называется расчленение множества единиц изучаемой совокупности на группы по определенным существенным для них признакам.
Например, все предприятия следует объединить в группы по отраслям промышленности, назначению выпускаемой продукции, численности занятых, форме собственности и т.д.
Принципы построения статистических группировок и классификаций
Классификацией называется систематизированное распределение явлений на определенные группы, классы, разряды на основании их сходства и различий.Перечислим отличительные черты классификации:
1) в основу ее кладется качественный признак;
2) классификации стандартны. Они устанавливаются органами государственной и международной статистики;
3) классификации устойчивы (то есть остаются неизменными в течение длительного периода времени).
Если группировка проводится по количественному признаку, то необходимо обратить особое внимание на число единиц исследуемого объекта и степень колеблемости группировочного признака.
При использовании персональных компьютеров для обработки статистических данных группировка единиц объекта производится с помощью стандартных процедур.
Одна из таких процедур основана на использовании формулы Стерджесса для определения оптимального числа групп:
, | (2.1) |
где n – число групп, N – число единиц совокупности.
Согласно формуле (2.1) выбор числа групп зависит от объема совокупности.
Недостаток формулы состоит в том, что ее применение дает хорошие результаты, если совокупность состоит из большого числа единиц, и распределение единиц по признаку, положенному в основание группировки, близко к нормальному.
Другой способ определения числа групп основан на применении показателя среднего квадратического отклонения (s). Если величина интервала групп равна 0,5 s, то совокупность разбивается на 12 групп, а когда величина равно 2/3 s и s, то совокупность делится соответственно на 9 и 6 групп. Если совокупность разбивается на 12 групп, то интервалы строятся следующим образом:
от – 3,0 s до –2,5 s
от – 2,5 s до – 2,0 s
от –2,0 s до – 1,5 s
от – 1,5 s до – 1,0 s
от –1,0 s до –0,5 s
от – 0,5 s до
от до + 0,5 s
от + 0,5 s до + 1,0 s
от + 1,0 s до + 1,5 s
от + 1,5 s до + 2,0 s
от + 2,0 s до + 2,5 s
от + 2,5 s до + 3,0 s,
где – среднее значение признака по совокупности, которое определяется по формуле , где – -е значение признака, s – среднеквадратическое отклонение .
Эти методы могут образовать «пустые» или малочисленные группы, в которые не попала ни одна единица совокупности. Наличие таких интервалов свидетельствует неправильности построения группировки.
После определения числа групп, например по формуле Стерджесса, следует определить интервал группировки.
Интервал – это значения варьирующего признака, лежащие в определенных границах. Каждый интервал имеет свою величину, верхнюю и нижнюю границы или хотя бы одну из них. Нижней границей интервала называется наименьшее значение признака в интервале, а верхней границей – наибольшее значение признака в нем. Величина интервала (или интервальная разность) представляет собой разность между верхней и нижней границами интервала. Интервалы группировки бывают равные и неравные. Последние делятся на прогрессивно возрастающие, прогрессивно убывающие, произвольные и специализированные. Если величина признака проявляется в сравнительно узких границах, и распределение носит равномерный характер, то строят группировку с равными интервалами. Величина равного интервала определяется по формуле:
, | (2.2) |
где – размах вариации, Xmax, Xmin – максимальное и минимальное значения признака в совокупности, а n – число групп.
Прежде чем определить размах вариации, из совокупности необходимо исключить аномальные наблюдения.
Полученную по формуле (2.2) величину округляют. Она является шагом интервала.
Существуют следующие правила определения шага интервала. Если величина интервала, рассчитанная по формуле (2.2) представляет собой величину, имеющую один знак до запятой (например 0,66; 1,372; 5,8), то полученные значения целесообразно округлить до десятых и использовать их в качестве шага интервала. В приведенном примере шагом интервала будут соответственно значения: 0,7; 1,4; 5,8.
Когда рассчитанная величина интервала имеет две значащие цифры до запятой и несколько знаков после запятой, то это значение надо округлить до целого числа. Например: 12,785; 15,01; 13; 15.
В случае, когда рассчитанная величина интервала представляет собой трехзначное, четырехзначное и так далее число, эту величину необходимо округлить до ближайшего числа, кратного 100 или 50. Например 248 следует округлить до 250.
Рассмотрим пример. Необходимо произвести группировку с равными интервалами предприятий по стоимости основных фондов, при этом максимальное значение признака Xmax=2040 млн. руб., а минимальное его значение – Xmin=290 млн. руб. Совокупность включает 80 единиц. Согласно формуле (2.1) она должна быть разбита на 7 групп. Сначала следует найти
R = 2040-290=1750 млн. руб.
Определим величину интервала: млн. руб.
После этого построим интервалы групп (табл. 2.5.).
Таблица 2.5
Варианты построения групп
№ групп | I вариант | II вариант |
I | От 290 до 540 | До 540 |
II | от 540 до 790 | 540 – 790 |
III | от 790 до 1040 | 790 – 1040 |
IV | от 1040 до 1290 | 1040 – 1290 |
V | от 1290 до 1540 | 1290 – 1540 |
VI | от 1540 до 1790 | 1540 – 1790 |
VII | от 1790 до 2040 | 1790 и более |
Чтобы не писать каждый раз "от … до", границы групп обозначают следующим образом: 290 – 540, 540 – 790 и т.д. Особенностью первого варианта построения групп является то, что у всех групп имеются закрытые интервалы. Во втором варианте первая и последняя группы – это группы с открытыми интервалами. Открытые – это те интервалы, у которых указана только одна граница (верхняя – у первого, нижняя – у последнего). Закрытыми называются интервалы, у которых обозначены обе границы. Ширина открытого интервала принимается равной ширине смежного с ним интервала. Если основанием группировки служит непрерывный признак, то одно и то же значение признака выступает и верхней, и нижней границами у двух смежных интервалов. Нижнюю границу формируем по принципу «включительно», а верхнюю по принципу «исключительно». Так, во втором интервале значение 540 включаем в интервал, а значение 790 не включаем во второй интервал.
Если в основании группировки лежит дискретный признак, то нижняя граница -го интервала равна верхней границе ( – 1)-го интервала, увеличенной на 1. Например, пусть совокупность состоит из 80 предприятий, и ее надо разделить на группы по численности занятых. Минимальное и максимальное значения группировочного признака соответственно равны 290 и 2040 человек. В этом случае возможен следующий вариант построения группы (табл. 2.6).
Таблица 2.6
Вариант построения группы
№ групп | Вариант |
I | До 540 |
II | 541 – 790 |
III | 791 – 1040 |
IV | 1041 – 1290 |
V | 1291 – 1540 |
VI | 1541 – 1790 |
VII | 1791 и более |
Далее рассмотрим неравные интервалы.
Неравные интервалы могут быть прогрессивно возрастающие или убывающие в арифметической или геометрической прогрессии. Величина интервалов, изменяющихся в арифметической прогрессии, определяется следующим образом:
, | (2.3) |
в геометрической прогрессии:
, | (2.4) |
где a – константа, a > 0 при прогрессивно возрастающих интервалах, a < 0 при прогрессивно убывающих интервалах; q – константа, q > 0, q > 1 при прогрессивно возрастающих интервалах, q < 1 при прогрессивно убывающих интервалах.
Например, если необходимо построить группировку предприятий отрасли по показателю выручки от реализации продукции, которая варьирует от 500 млн. руб. до 4000 млн. руб., то строить группы с равными интервалами нецелесообразно, потому что распределение числа предприятий по величине выручки является неравномерным. Строим группировку с неравными интервалами (табл. 2.7).
Таблица 2.7
Группировка с неравными интервалами
№ групп | Интервалы |
I | 500 – 800 |
II | 800 – 1300 |
III | 1300 – 2000 |
IV | 2000 – 2900 |
V | 2900 – 4000 |
Величина каждого последующего интервала у этой группировки больше предыдущего интервала на 200 млн. руб., то есть увеличивается в арифметической прогрессии.
При изучении социально – экономических явлений на макроуровне часто применяют группировки, интервалы которых не будут ни прогрессивно возрастающими, ни прогрессивно убывающими. Такие интервалы называются произвольными, например при обработке материалов переписи населения в 1989 г. для группировки семей и одиночек по размеру жилой площади, приходящейся на одного человека (м2), применялись следующие группы: до 5; 5–6; 7–8; 9–12; 13–14; 15–19; 20 и более.
После определения группировочного признака и границ групп строится ряд распределения.