Пример решения матричной игры методом линейного программирования
Решить матричную игру, заданную приведенной ниже матрицей, сведя ее к паре двойственных задач линейного программирования.| Игроки | B1 | B2 | B3 | B4 | B5 | a = min(Ai) |
| A1 | 5 | -8 | 7 | -6 | 0 | -8 |
| A2 | 8 | -5 | 9 | -3 | 2 | -5 |
| A3 | -2 | 7 | -3 | 6 | -4 | -4 |
| b = max(Bi ) | 8 | 7 | 9 | 6 | 2 | 0 |
Решение находим с помощью калькулятора.
Рассмотрим игру двух лиц, интересы которых противоположны. Такие игры называют антагонистическими играми двух лиц. В этом случае выигрыш одного игрока равен проигрышу второго, и можно описать только одного из игроков.
Предполагается, что каждый игрок может выбрать только одно из конечного множества своих действий. Выбор действия называют выбором стратегии игрока.
Если каждый из игроков выбрал свою стратегию, то эту пару стратегий называют ситуацией игры. Следует заметить, каждый игрок знает, какую стратегию выбрал его противник, т.е. имеет полную информацию о результате выбора противника.
Чистой стратегией игрока I является выбор одной из n строк матрицы выигрышей А, а чистой стратегией игрока II является выбор одного из столбцов этой же матрицы.
1. Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях.
Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.
| Игроки | B1 | B2 | B3 | B4 | B5 | a = min(Ai) |
| A1 | 5 | -8 | 7 | -6 | 0 | -8 |
| A2 | 8 | -5 | 9 | -3 | 2 | -5 |
| A3 | -2 | 7 | -3 | 6 | -4 | -4 |
| b = max(Bi) | 8 | 7 | 9 | 6 | 2 |
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = -4, которая указывает на максимальную чистую стратегию A3.
Верхняя цена игры b = min(bj) = 2.
Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах -4 ≤ y ≤ 2. Находим решение игры в смешанных стратегиях. Объясняется это тем, что игроки не могут объявить противнику свои чистые стратегии: им следует скрывать свои действия. Игру можно решить, если позволить игрокам выбирать свои стратегии случайным образом (смешивать чистые стратегии).
2. Проверяем платежную матрицу на доминирующие строки и доминирующие столбцы.
Иногда на основании простого рассмотрения матрицы игры можно сказать, что некоторые чистые стратегии могут войти в оптимальную смешанную стратегию лишь с нулевой вероятностью.
Говорят, что i-я стратегия 1-го игрока доминирует его k-ю стратегию, если aij ≥ akj для всех j Э N и хотя бы для одного j aij > akj. В этом случае говорят также, что i-я стратегия (или строка) – доминирующая, k-я – доминируемая.
Говорят, что j-я стратегия 2-го игрока доминирует его l-ю стратегию, если для всех j Э M aij ≤ ail и хотя бы для одного i aij < ail. В этом случае j-ю стратегию (столбец) называют доминирующей, l-ю – доминируемой.
Стратегия A2 доминирует над стратегией A1 (все элементы строки 2 больше или равны значениям 1-ой строки), следовательно, исключаем 1-ую строку матрицы. Вероятность p1 = 0.
| 8 | -5 | 9 | -3 | 2 |
| -2 | 7 | -3 | 6 | -4 |
С позиции проигрышей игрока В стратегия B5 доминирует над стратегией B1 (все элементы столбца 5 меньше элементов столбца 1), следовательно, исключаем 1-й столбец матрицы. Вероятность q1 = 0.
С позиции проигрышей игрока В стратегия B5 доминирует над стратегией B3 (все элементы столбца 5 меньше элементов столбца 3), следовательно, исключаем 3-й столбец матрицы. Вероятность q3 = 0.
| -5 | -3 | 2 |
| 7 | 6 | -4 |
Мы свели игру 3 x 5 к игре 2 x 3.
Так как игроки выбирают свои чистые стратегии случайным образом, то выигрыш игрока I будет случайной величиной. В этом случае игрок I должен выбрать свои смешанные стратегии так, чтобы получить максимальный средний выигрыш.
Аналогично, игрок II должен выбрать свои смешанные стратегии так, чтобы минимизировать математическое ожидание игрока I.
В матрице присутствуют отрицательные элементы. Для упрощения расчетов добавим к элементам матрицы (5). Такая замена не изменит решения игры, изменится только ее цена (по теореме фон Неймана).
| 0 | 2 | 7 |
| 12 | 11 | 1 |
3. Находим решение игры в смешанных стратегиях.
Математические модели пары двойственных задач линейного программирования можно записать так:
найти минимум функции F(x) при ограничениях (для игрока II):
12x2 ≥ 1
2x1+11x2 ≥ 1
7x1+x2 ≥ 1
F(x) = x1+x2 > min
найти максимум функции Z(y) при ограничениях (для игрока I):
2y2+7y3 ≤ 1
12y1+11y2+y3 ≤ 1
Z(y) = y1+y2+y3 > max
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.
Определим максимальное значение целевой функции Z(Y) = y1+y2+y3 при следующих условиях-ограничений.
2y2+7y3≤1
12y1+11y2+y3≤1
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
2y2+7y3+y4 = 1
12y1+11y2+y3+y5 = 1
Решим систему уравнений относительно базисных переменных: y4, y5
Полагая, что свободные переменные равны 0, получим первый опорный план:
Y0 = (0,0,0,1,1)
| Базис | B | y1 | y2 | y3 | y4 | y5 |
| y4 | 1 | 0 | 2 | 7 | 1 | 0 |
| y5 | 1 | 12 | 11 | 1 | 0 | 1 |
| Z(Y0) | 0 | -1 | -1 | -1 | 0 | 0 |
Переходим к основному алгоритму симплекс-метода.
Итерация №0.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
В качестве ведущего выберем столбец, соответствующий переменной y3, так как это наибольший коэффициент по модулю.
Вычислим значения Di по строкам как частное от деления: bi / ai3
и из них выберем наименьшее:
min (1 : 7 , 1 : 1 ) = 1/7
Следовательно, 1-ая строка является ведущей.
Разрешающий элемент равен (7) и находится на пересечении ведущего столбца и ведущей строки.
| Базис | B | y1 | y2 | y3 | y4 | y5 | min |
| y4 | 1 | 0 | 2 | 7 | 1 | 0 | 1/7 |
| y5 | 1 | 12 | 11 | 1 | 0 | 1 | 1 |
| Z(Y1) | 0 | -1 | -1 | -1 | 0 | 0 |
Формируем следующую часть симплексной таблицы. Вместо переменной y4 в план 1 войдет переменная y3.
Получаем новую симплекс-таблицу:
| Базис | B | y1 | y2 | y3 | y4 | y5 |
| y3 | 1/7 | 0 | 2/7 | 1 | 1/7 | 0 |
| y5 | 6/7 | 12 | 75/7 | 0 | -1/7 | 1 |
| Z(Y1) | 1/7 | -1 | -5/7 | 0 | 1/7 | 0 |
Итерация №1.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
В качестве ведущего выберем столбец, соответствующий переменной y1, так как это наибольший коэффициент по модулю.
Вычислим значения Di по строкам как частное от деления: bi / ai1
и из них выберем наименьшее:
min (- , 6/7 : 12 ) = 1/14
Следовательно, 2-ая строка является ведущей.
Разрешающий элемент равен (12) и находится на пересечении ведущего столбца и ведущей строки.
| Базис | B | y1 | y2 | y3 | y4 | y5 | min |
| y3 | 1/7 | 0 | 2/7 | 1 | 1/7 | 0 | - |
| y5 | 6/7 | 12 | 75/7 | 0 | -1/7 | 1 | 1/14 |
| Z(Y2) | 1/7 | -1 | -5/7 | 0 | 1/7 | 0 |
Формируем следующую часть симплексной таблицы. Вместо переменной y5 в план 2 войдет переменная y1.
Получаем новую симплекс-таблицу:
| Базис | B | y1 | y2 | y3 | y4 | y5 |
| y3 | 1/7 | 0 | 2/7 | 1 | 1/7 | 0 |
| y1 | 1/14 | 1 | 25/28 | 0 | -1/84 | 1/12 |
| Z(Y2) | 3/14 | 0 | 5/28 | 0 | 11/84 | 1/12 |
Конец итераций: индексная строка не содержит отрицательных элементов - найден оптимальный план
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.
Окончательный вариант симплекс-таблицы:
| Базис | B | y1 | y2 | y3 | y4 | y5 |
| y3 | 1/7 | 0 | 2/7 | 1 | 1/7 | 0 |
| y1 | 1/14 | 1 | 25/28 | 0 | -1/84 | 1/12 |
| Z(Y3) | 3/14 | 0 | 5/28 | 0 | 11/84 | 1/12 |
y1 = 1/14, y2 = 0, y3 = 1/7
Z(Y) = 1*1/14 + 1*0 + 1*1/7 = 3/14
Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи.
x1=11/84, x2= 1/12
Это же решение можно получить, применив теоремы двойственности.
Из теоремы двойственности следует, что X = C*A-1.
Составим матрицу A из компонентов векторов, входящих в оптимальный базис.
| A = (A3, A1) = |
|
Определив обратную матрицу D = А-1 через алгебраические дополнения, получим:
| D = A-1 = |
|
Как видно из последнего плана симплексной таблицы, обратная матрица A-1 расположена в столбцах дополнительных переменных.
Тогда X = C*A-1 =
| (1, 1) x |
| = (11/84;1/12) |
Оптимальный план двойственной задачи равен:
x1 = 11/84, x2 = 1/12
F(X) = 1*11/84+1*1/12 = 3/14
Цена игры будет равна g = 1/F(x), а вероятности применения стратегий игроков:
qi = g*yi; pi = g*xi.
Цена игры: g = 1 : 3/14 = 14/3
p1 = 14/3*11/84 = 11/18
p2 = 14/3*1/12 = 7/18
Оптимальная смешанная стратегия игрока I: P = (11/18; 7/18)
q1 = 14/3*1/14 = 1/3
q2 = 14/3*0 = 0
q3 = 14/3*1/7 = 2/3
Оптимальная смешанная стратегия игрока II: Q = (1/3; 0; 2/3)
Поскольку ранее к элементам матрицы было прибавлено число (5), то вычтем это число из цены игры.
42/3 - 5 = -1/3
Цена игры: v=-1/3
4. Проверим правильность решения игры с помощью критерия оптимальности стратегии.
∑aijqj ≤ v
∑aijpi ≥ v
M(P1;Q) = (-5*1/3) + (-3*0) + (2*2/3) = -0.333 = v
M(P2;Q) = (7*1/3) + (6*0) + (-4*2/3) = -0.333 = v
M(P;Q1) = (-5*11/18) + (7*7/18) = -0.333 = v
M(P;Q2) = (-3*11/18) + (6*7/18) = 0.5 ≥ v
M(P;Q3) = (2*11/18) + (-4*7/18) = -0.333 = v
Все неравенства выполняются как равенства или строгие неравенства, следовательно, решение игры найдено верно.
Поскольку из исходной матрицы были удалены строки и столбцы, то найденные векторы вероятности можно записать в виде:
P(0,11/18,7/18)
Q(0,1/3,0,0,2/3)
Пример №2. Решить матричную игру методом линейного программирования.
| 6 | 5 | 7 |
| 10 | 4 | 7 |
| 13 | 10 | 4 |
| 7 | 11 | 5 |
Решение находим через сервис матричная игра.
| A/B | B1 | B2 | B3 | a = min(Ai) |
| A1 | 6 | 5 | 7 | 5 |
| A2 | 10 | 4 | 7 | 4 |
| A3 | 13 | 10 | 4 | 4 |
| A4 | 7 | 11 | 5 | 5 |
| b = max(Bi ) | 13 | 11 | 7 | 0 |
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = 5, которая указывает на максимальную чистую стратегию A1.
Верхняя цена игры b = min(bj) = 7.
Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах 5 <= y <= 7. Находим решение игры в смешанных стратегиях..
Математические модели пары двойственных задач линейного программирования можно записать так:
найти минимум функции F(x) при ограничениях:
6x1+10x2+13x3+7x4 >= 1
5x1+4x2+10x3+11x4 >= 1
7x1+7x2+4x3+5x4 >= 1
F(x) = x1+x2+x3+x4 = min
найти максимум функции Ф(y) при ограничениях:
6y1+5y2+7y3 <= 1
10y1+4y2+7y3 <= 1
13y1+10y2+4y3 <= 1
7y1+11y2+5y3 <= 1
Ф(y) = y1+y2+y3 = max
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.
Определим минимальное значение целевой функции F(X) = x1 + x2 + x3 + x4 при следующих условиях-ограничений.
6x1 + 10x2 + 13x3 + 7x4≥1
5x1 + 4x2 + 10x3 + 11x4≥1
7x1 + 7x2 + 4x3 + 5x4≥1
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
6x1 + 10x2 + 13x3 + 7x4-1x5 + 0x6 + 0x7 = 1
5x1 + 4x2 + 10x3 + 11x4 + 0x5-1x6 + 0x7 = 1
7x1 + 7x2 + 4x3 + 5x4 + 0x5 + 0x6-1x7 = 1
Поскольку задача решается на минимум и элементы единичной матрицы отрицательны, сведем задачу к нахождению максимума. Для этого умножим все строки на (-1) и будем искать первоначальный опорный план.
-6x1-10x2-13x3-7x4 + 1x5 + 0x6 + 0x7 = -1
-5x1-4x2-10x3-11x4 + 0x5 + 1x6 + 0x7 = -1
-7x1-7x2-4x3-5x4 + 0x5 + 0x6 + 1x7 = -1
Решим систему уравнений относительно базисных переменных: x5, x6, x7,
Полагая, что свободные переменные равны 0, получим первый опорный план: X1 = (0,0,0,0,-1,-1,-1)
| План | Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| 0 | x5 | -1 | -6 | -10 | -13 | -7 | 1 | 0 | 0 |
| x6 | -1 | -5 | -4 | -10 | -11 | 0 | 1 | 0 | |
| x7 | -1 | -7 | -7 | -4 | -5 | 0 | 0 | 1 | |
| Индексная строка | F(X0) | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
В столбце свободных членов есть отрицательные элементы. Используем двойственный симплекс-метод. Выберем из них наибольший по модулю, а в его строке – любой отрицательный. Взяв этот элемент в качестве разрешающего пересчитаем таблицу.
В качестве ведущего выберем столбец, соответствующий переменной x1.
1-ая строка является ведущей.
| План | Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| x1 | 1 /6 | 1 | 12/3 | 21/6 | 11/6 | -1 /6 | 0 | 0 | |
| x6 | -1 /6 | 0 | 41/3 | 5 /6 | -51/6 | -5 /6 | 1 | 0 | |
| x7 | 1 /6 | 0 | 42/3 | 111/6 | 31/6 | -11/6 | 0 | 1 | |
| Индексная строка | F(X) | -1 /6 | 0 | -2 /3 | -11/6 | -1 /6 | 1 /6 | 0 | 0 |
Посмотреть все итерации
Конец итераций: индексная строка не содержит отрицательных элементов - найден оптимальный план
Окончательный вариант симплекс-таблицы:
| План | Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| 3 | x1 | 24 /227 | 1 | 0 | -1196/227 | 0 | 57 /227 | 1 /227 | -82 /227 |
| x4 | 9 /227 | 0 | 0 | 140/227 | 1 | -7 /227 | -28 /227 | 26 /227 | |
| x2 | 2 /227 | 0 | 1 | 1135/227 | 0 | -52 /227 | 19 /227 | 31 /227 | |
| Индексная строка | F(X3) | -35 /227 | 0 | 0 | 21 /227 | 0 | 2 /227 | 8 /227 | 25 /227 |
F(X) = 1•24/227 + 1•2/227 = 35/227
Составим двойственную задачу к прямой задаче.
6y1 + 5y2 + 7y3≤1
10y1 + 4y2 + 7y3≤1
13y1 + 10y2 + 4y3≤1
7y1 + 11y2 + 5y3≤1
y1 + y2 + y3 → max
y1 ≥ 0, y2 ≥ 0, y3 ≥ 0
Данную двойственную задачу можно решить двумя способами – используя снова прямой симплексный метод и воспользовавшись теоремой двойственности.
Первый способ нахождений двойственной задачи
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.Определим максимальное значение целевой функции F(X) = x1 + x2 + x3 при следующих условиях-ограничений.
6x1 + 5x2 + 7x3≤1
10x1 + 4x2 + 7x3≤1
13x1 + 10x2 + 4x3≤1
7x1 + 11x2 + 5x3=1
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
6x1 + 5x2 + 7x3 + 1x4 + 0x5 + 0x6 = 1
10x1 + 4x2 + 7x3 + 0x4 + 1x5 + 0x6 = 1
13x1 + 10x2 + 4x3 + 0x4 + 0x5 + 1x6 = 1
7x1 + 11x2 + 5x3 + 0x4 + 0x5 + 0x6 = 1
Введем искусственные переменные x.
6x1 + 5x2 + 7x3 + 1x4 + 0x5 + 0x6 + 0x7= 1
10x1 + 4x2 + 7x3 + 0x4 + 1x5 + 0x6 + 0x7= 1
13x1 + 10x2 + 4x3 + 0x4 + 0x5 + 1x6 + 0x7= 1
7x1 + 11x2 + 5x3 + 0x4 + 0x5 + 0x6 + 1x7= 1
Для постановки задачи на максимум целевую функцию запишем так:
F(X) = x1+x2+x3 - Mx7 => max
За использование искусственных переменных, вводимых в целевую функцию, накладывается так называемый штраф величиной М, очень большое положительное число, которое обычно не задается.
Полученный базис называется искусственным, а метод решения называется методом искусственного базиса.
Причем искусственные переменные не имеют отношения к содержанию поставленной задачи, однако они позволяют построить стартовую точку, а процесс оптимизации вынуждает эти переменные принимать нулевые значения и обеспечить допустимость оптимального решения.
Из уравнений выражаем искусственные переменные:
x7 = 1-7x1-11x2-5x3
которые подставим в целевую функцию:
F(X) = x1 + x2 + x3 - M(1-7x1-11x2-5x3) => max
или
F(X) = (1+7M)x1+(1+11M)x2+(1+5M)x3+(-1M) => max
Посмотреть решение
Оптимальный план можно записать так:
x3 = 25/227
x1 = 2/227
x6 = 21/227
x2 = 8/227
F(X) = 1•25/227 + 1•2/227 + 1•8/227 = 35/227
Второй способ нахождений двойственной задачи
Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи.Из теоремы двойственности следует, что Y = C*A-1.
Составим матрицу A из компонентов векторов, входящих в оптимальный базис.
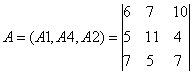
Определив обратную матрицу А-1 через алгебраические дополнения, получим:
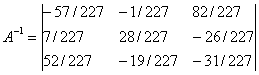
Тогда
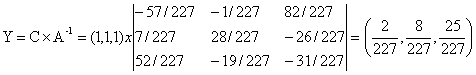
y1 = 2/227
y2 = 8/227
y3 = 25/227
Z(Y) = 1*2/227+1*8/227+1*25/227= 35/227
Оптимальный план двойственной задачи равен:
y1 = 2/227
y2 = 8/227
y3 = 25/227
Z(Y) = 1*2/227+1*8/227+1*25/227= 35/227
Цена игры будет равна g = 1/F(x), а вероятности применения стратегий игроков:
pi = g*xi; qi = g*yi.
Цена игры: g = 1 : 35/227 = 617/35
p1 = 617/35 • 24/227 = 24/35
p2 = 617/35 • 2/227 = 2/35
p3 = 617/35 • 0 = 0
p4 = 617/35 • 9/227 = 9/35
Оптимальная смешанная стратегия игрока I:
P = (24/35; 2/35; 0; 9/35)
q1 = 617/35 • 2/227 = 2/35
q2 = 617/35 • 8/227 = 8/35
q3 = 617/35 • 25/227 = 5/7
Оптимальная смешанная стратегия игрока II:
Q = (2/35; 8/35; 5/7)
Перейти к онлайн решению своей задачи
Решение матричной игры симплексным методом
Найти решение матричной игры. Решить матричные игры симплексным методом.Задание. Свести задачу, заданную платежной матрицей, к задаче линейного программирования (предварительно упростив задачу, убрав строго доминируемые стратегии, если это возможно) и решить симплекс методом.
Решение проводим с помощью калькулятора.
| Игроки | B1 | B2 | B3 | a = min(Ai) |
| A1 | 0 | 3 | 1 | 0 |
| A2 | 3 | 0 | 5 | 0 |
| A3 | 2 | 1 | 1 | 1 |
| b = max(Bi ) | 3 | 3 | 5 | 0 |
Верхняя цена игры b = min(bj) = 3.
Что свидетельствует об отсутствии седловой точки, так как a<>b, тогда цена игры находится в пределах 1 <= y <= 3. Находим решение игры в смешанных стратегиях..
Приведем матричную игру к задаче линейного программирования. Математические модели пары двойственных задач линейного программирования можно записать так:
найти минимум функции F(x) при ограничениях:
3x2+2x3 >= 1
3x1+x3 >= 1
x1+5x2+x3 >= 1
F(x) = x1+x2+x3 = min
найти максимум функции Ф(y) при ограничениях:
3y2+y3 <= 1
3y1+5y3 <= 1
2y1+y2+y3 <= 1
Ф(y) = y1+y2+y3 = max
Решаем эти системы двойственным симплекс-методом.
Определим минимальное значение целевой функции F(X) = x1 + x2 + x3 при следующих условиях-ограничений.
3x2 + 2x3≥1
3x1 + x3≥1
x1 + 5x2 + x3≥1
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
0x1 + 3x2 + 2x3-1x4 + 0x5 + 0x6 = 1
3x1 + 0x2 + 1x3 + 0x4-1x5 + 0x6 = 1
1x1 + 5x2 + 1x3 + 0x4 + 0x5-1x6 = 1
Поскольку задача решается на минимум и элементы единичной матрицы отрицательны, сведем задачу к нахождению максимума. Для этого умножим все строки на (-1) и будем искать первоначальный опорный план.
0x1-3x2-2x3 + 1x4 + 0x5 + 0x6 = -1
-3x1 + 0x2-1x3 + 0x4 + 1x5 + 0x6 = -1
-1x1-5x2-1x3 + 0x4 + 0x5 + 1x6 = -1
Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.
Решим систему уравнений относительно базисных переменных: x4, x5, x6,
Полагая, что свободные переменные равны 0, получим первый опорный план: X1 = (0,0,0,-1,-1,-1)
| План | Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
| 0 | x4 | -1 | 0 | -3 | -2 | 1 | 0 | 0 |
| x5 | -1 | -3 | 0 | -1 | 0 | 1 | 0 | |
| x6 | -1 | -1 | -5 | -1 | 0 | 0 | 1 | |
| Индексная строка | F(X0) | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
Посмотреть решение
Оптимальный план можно записать так:
x2 = 1/3, x1 = 1/3, x6 = 1
F(X) = 1•1/3 + 1•1/3 = 2/3
Составим двойственную задачу к прямой задаче.
3y2 + y3≤1
3y1 + 5y3≤1
2y1 + y2 + y3≤1
y1 + y2 + y3 => max
y1 ≥ 0, y2 ≥ 0, y3 ≥ 0
Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи.
Из теоремы двойственности следует, что Y = C*A-1.
Составим матрицу A из компонентов векторов, входящих в оптимальный базис.
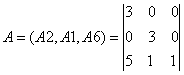
Определив обратную матрицу А-1 через алгебраические дополнения, получим:
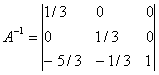
Как видно из последнего плана симплексной таблицы, обратная матрица A-1 расположена в столбцах дополнительных переменных .
Тогда Y = C*A-1 = 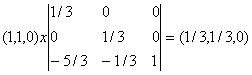
Оптимальный план двойственной задачи равен:
y1 = 1/3, y2 = 1/3, y3 = 0
Z(Y) = 1*1/3+1*1/3+1*0 = 2/3
Цена игры будет равна g = 1/F(x), а вероятности применения стратегий игроков:
pi = g*xi; qi = g*yi.
Цена игры: g = 1 : 2/3 = 11/2
p1 = 11/2 • 1/3 = 1/2
p2 = 11/2 • 1/3 = 1/2
p3 = 11/2 • 0 = 0
q1 = 11/2 • 1/3 = 1/2
q2 = 11/2 • 1/3 = 1/2
q3 = 11/2 • 0 = 0
Оптимальная стратегия игрока А: P(1/2 ; 1/2;0)
Оптимальная стратегия игрока B: Q(1/2; 1/2;0)
Перейти к онлайн решению своей задачи
Пример №3. Предприятие выпускает скоропортящуюся продукцию, которую сразу можно доставить потребителю (А1 стратегия). Отправить на склад для хранения (А2 стратегия) или подвергнуть обработке для длит. Хранения (А3 стратегия) . Потребитель может приобрести немедленно (В1 стратег) ,через некоторое время (В2 стратег) или после длительного периода (В3 стратегия).
В случае стратегий А2 и А3 предприятие несет дополнительные затраты на хранение и обработку продукции. Однако, при А2 следует вычесть убытки, если потребитель выберет стратегию В2 или В3 . Определить оптимальные пропорции для применения стратегий А1,А2,А3. Руководствуясь минимаксным критерием, гарантирует средний уровень убытка. Пользуясь минимальным критерием из таблицы.
| Игроки | B1 | B2 | B3 | a = min(Ai) |
| A1 | 2 | 3 | 2 | 2 |
| A2 | 4 | 2 | 1 | 1 |
| A3 | 1 | 3 | 3 | 1 |
| b = max(Bi ) | 4 | 3 | 3 | 0 |
Решение матричной игры находим через сервис решение матричной игры.
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = 2, которая указывает на максимальную чистую стратегию A1.
Верхняя цена игры b = min(bj) = 3.
Что свидетельствует об отсутствии седловой точки, так как a<>b, тогда цена игры находится в пределах 2 <= y <= 3. Находим решение игры в смешанных стратегиях. Переходим к этапу сведения матричной игры к задаче линейного программирования.
Математические модели пары двойственных задач линейного программирования можно записать так:
найти минимум функции F(x) при ограничениях:
2x1+4x2+x3 >= 1
3x1+2x2+3x3 >= 1
2x1+x2+3x3 >= 1
F(x) = x1+x2+x3 = min
найти максимум функции Ф(y) при ограничениях:
2y1+3y2+2y3 <= 1
4y1+2y2+y3 <= 1
y1+3y2+3y3 <= 1
Ф(y) = y1+y2+y3 = max
Решаем эти системы симплекс-методом.
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.
Определим минимальное значение целевой функции F(X) = x1 + x2 + x3 при следующих условиях-ограничений.
2x1 + 4x2 + x3≥1
3x1 + 2x2 + 3x3≥1
2x1 + x2 + 3x3≥1
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
2x1 + 4x2 + 1x3-1x4 + 0x5 + 0x6 = 1
3x1 + 2x2 + 3x3 + 0x4-1x5 + 0x6 = 1
2x1 + 1x2 + 3x3 + 0x4 + 0x5-1x6 = 1
Поскольку задача решается на минимум и элементы единичной матрицы отрицательны, сведем задачу к нахождению максимума. Для этого умножим все строки на (-1) и будем искать первоначальный опорный план.
-2x1-4x2-1x3 + 1x4 + 0x5 + 0x6 = -1
-3x1-2x2-3x3 + 0x4 + 1x5 + 0x6 = -1
-2x1-1x2-3x3 + 0x4 + 0x5 + 1x6 = -1
Посмотреть все итерации
Оптимальный план можно записать так: x3 = 3/11, x5 = 2/11, x2 = 2/11
F(X) = 1•3/11 + 1•2/11 = 5/11
Оптимальный план двойственной задачи равен: y1 = 2/11, y2 = 0, y3 = 3/11
Z(Y) = 1*2/11+1*0+1*3/11 = 5/11
Цена игры будет равна g = 1/F(x), а вероятности применения стратегий игроков: pi = g*xi; qi = g*yi.
Цена игры: g = 1 : 5/11 = 21/5
p1 = 21/5•0 = 0
p2 = 21/5•2/11 = 2/5
p3 = 21/5•3/11 = 3/5
q1 = 21/5•2/11 = 2/5
q2 = 21/5•0 = 0
q3 = 21/5•3/11 = 3/5
Оптимальная стратегия игрока А: P( 0; 2/5; 3/5)
Оптимальная стратегия игрока B: Q(2/5;0;3/5)


