Т-критерий Вилкоксона
Критерий применяется для сопоставления показателей, измеренных в двух разных условиях на одной и той же выборке испытуемых.Он позволяет установить не только направленность изменений, но и их выраженность. С его помощью определяется, является ли сдвиг показателей в каком-то одном направлении более интенсивным, чем в другом.
Суть метода состоит в сопоставлении выраженности сдвигов в том и ином направлениях по абсолютной величине. Для этого сначала ранжируются все абсолютные величины сдвигов, а потом суммируются ранги. Если сдвиги в положительную и в отрицательную сторону происходят случайно, то суммы рангов абсолютных значений их будут примерно равны. Если же интенсивность сдвига в одном из направлений перевешивает, то сумма рангов абсолютных значений сдвигов в противоположную сторону будет значительно ниже, чем это могло бы быть при случайных изменениях.
Первоначально исходят из предположения о том, что типичным сдвигом будет сдвиг в более часто встречающемся направлении, а нетипичным, или редким, сдвигом– сдвиг в более редко встречающемся направлении.
Гипотезы.
H0: Интенсивность сдвигов в типичном направлении не превосходит интенсивности сдвигов в нетипичном направлении.
H1: Интенсивность сдвигов в типичном направлении превышает интенсивность сдвигов в нетипичном направлении.
Ограничения в применении Т-критерия Вилкоксона
- Минимальное количество испытуемых, прошедших измерения в двух условиях – 5 человек. Максимальное количество испытуемых– 50 человек, что диктуется верхней границей имеющихся таблиц.
- Нулевые сдвиги из рассмотрения исключаются, и количество наблюденийn уменьшается на количество этих нулевых сдвигов. Можно обойти это ограничение, сформулировав гипотезы, включающие отсутствие изменений, например: "Сдвиг в сторону увеличения значений превышает сдвиг в сторону уменьшения значений и тенденцию сохранения их на прежнем уровне".
Алгоритм подсчета Т-критерия Вилкоксона
- Составить список испытуемых в любом порядке, например, алфавитном.
- Вычислить разность между индивидуальными значениями во втором и первом замерах ("после" – "до"). Определить, что будет считаться"типичным" сдвигом и сформулировать соответствующие гипотезы.
- Перевести разности в абсолютные величины и записать их отдельным столбцом (иначе трудно отвлечься от знака разности).
- Проранжировать абсолютные величины разностей, начисляя меньшему значению меньший ранг. Проверить совпадение полученной суммы рангов с расчетной.
- Отметить кружками или другими знаками ранги, соответствующие сдвигам в"нетипичном" направлении.
- Подсчитать сумму этих рангов по формуле: Т=∑R{\\sub r}, где R{\\sub r} – ранговые значения сдвигов с более редким знаком.
- Определить критические значения Т для данного n по таблице.
Если Тэмп. меньше или равен Ткр., сдвиг в"типичную" сторону по интенсивности достоверно преобладает.
| № исп. | эксп. | контр. |
| 1 | 14 | 13 |
| 2 | 13 | 13 |
| 3 | 11 | 14 |
| 4 | 8 | 12 |
| 5 | 12 | 14 |
| 6 | 13 | 14 |
| 7 | 13 | 12 |
| 8 | 13 | 13 |
| 9 | 11 | 15 |
| 10 | 12 | 13 |
| 11 | 14 | 11 |
| 12 | 13 | 12 |
| 13 | 12 | 14 |
| 14 | 14 | 9 |
| 15 | 10 | 14 |
Решение. Для подсчета этого критерия нет необходимости упорядочивать ряды значений по нарастанию признака.
Первый шаг в подсчете T-критерия – вычитание каждого индивидуального значения "до" из значения"после".
| До измерения, tдо | После измерения, tпосле | Разность (tдо-tпосле) | Абсолютное значение разности |
| 14 | 13 | -1 | 1 |
| 13 | 13 | 0 | 0 |
| 11 | 14 | 3 | 3 |
| 8 | 12 | 4 | 4 |
| 12 | 14 | 2 | 2 |
| 13 | 14 | 1 | 1 |
| 13 | 12 | -1 | 1 |
| 13 | 13 | 0 | 0 |
| 11 | 15 | 4 | 4 |
| 12 | 13 | 1 | 1 |
| 14 | 11 | -3 | 3 |
| 13 | 12 | -1 | 1 |
| 12 | 14 | 2 | 2 |
| 14 | 9 | -5 | 5 |
| 10 | 14 | 4 | 4 |
Так как в матрице имеются связанные ранги (одинаковый ранговый номер) 1-го ряда, произведем их переформирование. Переформирование рангов производиться без изменения важности ранга, то есть между ранговыми номерами должны сохраниться соответствующие соотношения (больше, меньше или равно). Также не рекомендуется ставить ранг выше 1 и ниже значения равного количеству параметров (в данном случае n = 15). Переформирование рангов производится в табл.
| Номера мест в упорядоченном ряду | Расположение факторов по оценке эксперта | Новые ранги |
| 1 | 0 | 1.5 |
| 2 | 0 | 1.5 |
| 3 | 1 | 5 |
| 4 | 1 | 5 |
| 5 | 1 | 5 |
| 6 | 1 | 5 |
| 7 | 1 | 5 |
| 8 | 2 | 8.5 |
| 9 | 2 | 8.5 |
| 10 | 3 | 10.5 |
| 11 | 3 | 10.5 |
| 12 | 4 | 13 |
| 13 | 4 | 13 |
| 14 | 4 | 13 |
| 15 | 5 | 15 |
Гипотезы.
H0: Показатели после проведения опыта превышают значения показателей до эксперимента.
H1: Показатели после проведения опыта меньше значений показателей до эксперимента.
| До измерения, tдо | После измерения, tпосле | Разность (tдо-tпосле) | Абсолютное значение разности | Ранговый номер разности |
| 14 | 13 | -1 | 1 | 5 |
| 13 | 13 | 0 | 0 | 1.5 |
| 11 | 14 | 3 | 3 | 10.5 |
| 8 | 12 | 4 | 4 | 13 |
| 12 | 14 | 2 | 2 | 8.5 |
| 13 | 14 | 1 | 1 | 5 |
| 13 | 12 | -1 | 1 | 5 |
| 13 | 13 | 0 | 0 | 1.5 |
| 11 | 15 | 4 | 4 | 13 |
| 12 | 13 | 1 | 1 | 5 |
| 14 | 11 | -3 | 3 | 10.5 |
| 13 | 12 | -1 | 1 | 5 |
| 12 | 14 | 2 | 2 | 8.5 |
| 14 | 9 | -5 | 5 | 15 |
| 10 | 14 | 4 | 4 | 13 |
| Сумма | 120 |
Сумма по столбцу рангов равна ∑=120
Проверка правильности составления матрицы на основе исчисления контрольной суммы:
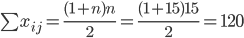
Сумма по столбцу и контрольная сумма равны между собой, значит, ранжирование проведено правильно.
Теперь отметим те направления, которые являются нетипичными, в данном случае – отрицательными. В Таблице эти направления и соответствующие им ранги выделены цветом. Сумма рангов этих «редких» направлений составляет эмпирическое значение критерия Т:
T=∑Rt=5+5+10.5+5+15=40.5
По таблице Приложения находим критические значения для Т-критерия Вилкоксона для n=15:
Tкр=19 (p≤0.01)
Tкр=30 (p≤0.05)
Зона значимости в данном случае простирается влево, действительно, если бы "редких", в данном случае положительных, направлений не было совсем, то и сумма их рангов равнялась бы нулю.
В данном же случае эмпирическое значение Т попадает в зону незначимости: Тэмп>Ткр(0,05).
Гипотеза H0 отвергается. Показатели после эксперимента не превышают значения показателей до опыта.
Критерий Вилкоксона для независимых выборок
Этот критерий используется для проверки однородности двух независимых выборок x1,x2,…,xn1 и y1,y2,…,yn2. Он применяется к случайным величинам, распределения которых неизвестны, но являются непрерывными.Основная гипотеза имеет вид H0: F1(x)=F2(x) а альтернативная гипотеза может быть левосторонней, правосторонней или двусторонней.
При использовании критерия Вилкоксона все вычисления проводятся не для самих наблюдаемых значений xi,yi а для их рангов. Ранг — это порядковый номер наблюдения в данной выборке, если наблюдаемые значения расположить по возрастанию.
Последовательность действий при проверке гипотезы однородности с помощью критерия Вилкоксона следующая:
1) составляем объединение выборок x1,x2,…,xn1 и y1,y2,…,yn2.
2) находим ранги объединенной выборки (обозначим ранги первой выборки r1,r2,..,rn1 а ранги второй - s1,s2,..,sn2)
3) вычисляем наблюдаемое значение статистики Вилкоксона равную сумме рангов второй выборки.
Если распределение второй выборки сдвинуто вправо относительно первой (альтернативная гипотеза H1: F1(x)<F2(x) то статистика K будет принимать значения, большие критического Kkp=K(n1,n2;α) и гипотеза H0 отвергается в пользу альтернативы H1
Если рассматривается альтернатива H1: F1(x)≠F2(x) то гипотеза H0 отвергается, если выполняется одно из двух условий: Kнабл>Kkp=K(n1,n2;α/2) или Kнабл=n2(n2+n1+1)-K(n1,n2;α/2).
Пример №2. В биохимическом исследовании, проведенном методом меченных атомов, по результатам изучения 7 препаратов опытной группы получены следующие показания счетчика импульсов (в импульсах в минуту): 340, 343, 322, 332, 320, 313, 304. Результаты контрольной группы: 318, 321, 318, 301, 312.
Можно ли считать, что полученные значения опытной и контрольной групп различны α=0.05.
Решение. Сформулируем основную и альтернативную гипотезы.
H0: F1(x)=F2(x) — выборки однородны; различия в результатах опытной и контрольной групп можно отнести на счет случайных воздействий.
H1: F1(x)≠F2(x) - выборки извлечены из генеральных совокупностей с разными распределениями; различие между контрольной и опытной группами существенно.
Объединим выборки и расположим полученные данные в порядке возрастания: 301, 304, 312, 313, 318, 318, 320, 321, 322, 332, 340, 343 — здесь подчеркнуты элементы второй выборки (контрольной группы). Занумеровав все элементы в порядке возрастания, получим ранговую последовательность: 1, 2, 3, 4, 5.5, 5.5, 7, 8, 9, 10, 11, 12 — подчеркнуты ранги контрольной группы.
Наблюдаемое значение статистики Вилкоксона равно
Kнабл=1+3+5,5+5,5+8=23
Критическая область является двусторонней, ее правая граница при α=0.1
Клев= n2(n2+n1+1)-Kпр=5*14-44=26.
Наблюдаемое значение попадает в критическую область: Kнабл< Клев поэтому основная гипотеза отвергается в пользу альтернативной.
Итак, на уровне значимости 0.1 можно утверждать, что разница между показаниями счетчика в контрольной и опытной группах существенна.
Критические точки критерия Вилкоксона при α=0.05
| n2 | n1 | |||
| 5 | 7 | 9 | 10 | |
| 5 | 36 | 44 | 51 | 54 |
Табличные значения T-критерия Вилкоксона
В таблице указаны критические значения T-критерия Вилкоксона в зависимости от уровня значимости.| N | p<0,05 | p<0,01 |
| 5 | 0 | — |
| 6 | 2 | — |
| 7 | 3 | 0 |
| 8 | 5 | 1 |
| 9 | 8 | 3 |
| 10 | 10 | 5 |
| 11 | 13 | 7 |
| 12 | 17 | 9 |
| 13 | 21 | 12 |
| 14 | 25 | 15 |
| 15 | 30 | 19 |
| 16 | 35 | 23 |
| 17 | 41 | 27 |
| 18 | 47 | 32 |
| 19 | 53 | 37 |
| 20 | 60 | 43 |
| 21 | 67 | 49 |
| 22 | 75 | 55 |
| 23 | 83 | 62 |
| 24 | 91 | 69 |
| 25 | 100 | 76 |
| 26 | 110 | 84 |
| 27 | 119 | 92 |
| 28 | 130 | 101 |
| 29 | 140 | 110 |
| 30 | 151 | 120 |
| 31 | 163 | 130 |
| 32 | 175 | 140 |
| 33 | 187 | 151 |
| 34 | 200 | 162 |
| 35 | 213 | 173 |
| 36 | 227 | 185 |
| 37 | 241 | 198 |
| 38 | 256 | 211 |
| 39 | 271 | 224 |
| 40 | 286 | 238 |
| 41 | 302 | 252 |
| 42 | 319 | 266 |
| 43 | 336 | 281 |
| 44 | 353 | 296 |
| 45 | 371 | 312 |
| 46 | 389 | 328 |
| 47 | 407 | 345 |
| 48 | 426 | 362 |
| 49 | 446 | 379 |
| 50 | 466 | 397 |
типичнуюсторону достоверное не преобладают.



